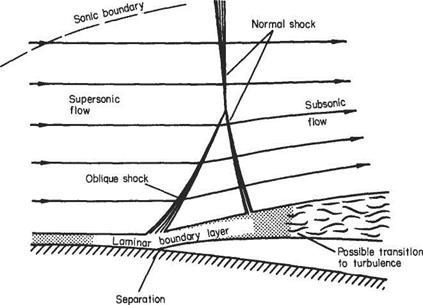
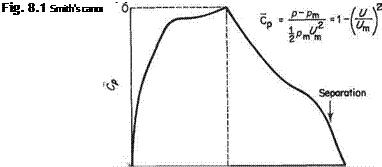
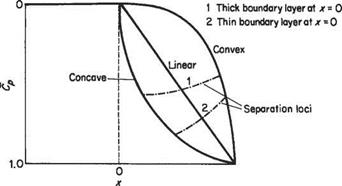
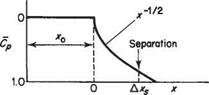
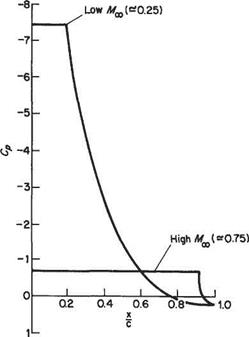
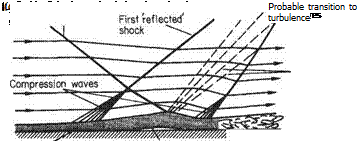
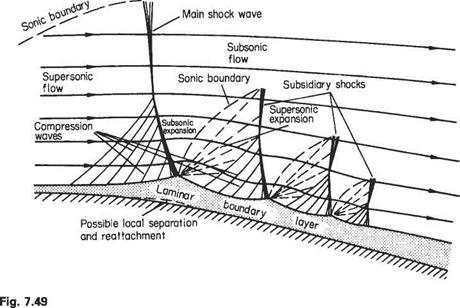
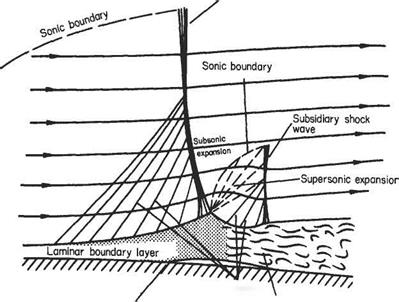
One of the main differences between subsonic and supersonic flows, as far as boundary-layer behaviour is concerned, is that the pressure gradient along the flow is of opposite sign with respect to cross-sectional area change. Thus in a converging supersonic flow the pressure rises and in a diverging flow the pressure falls in the stream direction (see Section 6.2). As a result the pressure gradient at a convex corner is negative and the boundary layer will generally negotiate the comer without separating, and the effect of the boundary layer on the external or mainstream flow will be negligible (Fig. 7.52a). Conversely, at a concave comer an oblique shock wave is generated and the corresponding pressure rise will cause boundary-layer thickening ahead of the shock, and in the case of a laminar boundary layer will probably cause local separation at the comer (see Figs 7.52b and 7.53). The resultant curvature of the flow just outside the boundary layer causes a wedge of compression wavelets to develop which, in effect, diffuse the base of the shock wave as shown in Fig. 7.52b.
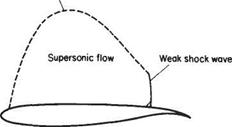
At the nose of a wedge, the oblique nose shock will be affected by the boundary- layer growth; the presence of the rapidly thickening boundary layer near the leading edge produces an effective curvature of the nose of the wedge and a small region of expansive (Prandtl-Meyer) flow will develop locally behind the nose shock, which will now be curved and slightly detached from the nose (Fig. 7.54a). A similar effect will occur at the leading edge of a flat plate where a small detached curved local shock will develop. This shock will rapidly degenerate into a very weak shock approximating to a Mach wave at a small distance from the leading edge (Fig. 7.54b).
In some cases, an oblique shock that has been generated at some other point in the mainstream may be incident on the surface and boundary layer. Such a shock will be at an angle, between the upstream surface and itself, of considerably less than 90°. The general reaction of the boundary layer to this condition is similar to that already discussed in the transonic case, except that the oblique shock does not, in general, reduce the mainstream flow to a subsonic speed.
If the boundary layer is turbulent, it appears to reflect the shock wave as another shock wave in much the same way as would the solid surface in the absence of the boundary layer, although some thickening of the boundary layer occurs. There may also be local separation and reattachment, in which case the reflected shock originates just
|
|
|

Fig. 7.53 Supersonic flow through a sharp concave corner: The flow is from left to right at a downstream Mach number of 2.5. The holographic interferogram shows flow turning through an angle of 11° thereby forming an oblique shock wave that interacts with the turbulent boundary layer present on the wall. Each fringe corresponds to constant density. The boundary layer transmits the effect of the shock wave a short distance upstream but there is no flow separation. Compare with Fig. 7.52b above. (The photograph was taken by P. J. Bryanston-Cross in the Engineering Department, University of Warwick, UK.)
|
|

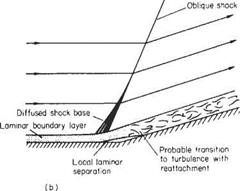
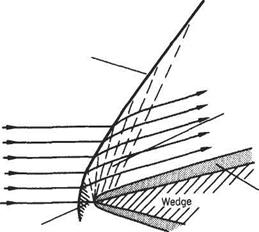
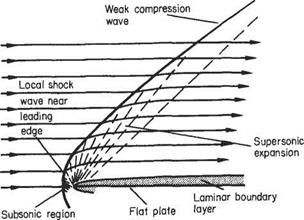
Fig. 7.54 ahead of the point of incidence. A laminar boundary layer, however, thickens gradually up to the point of incidence, and may separate locally in this region, and then rapidly become thinner again. The shock then reflects as a fan of expansion waves, followed by a diffused shock a little farther downstream. There is also a set of weak compression waves set up ahead of the incident shock, owing to the boundary-layer thickening, but these do not usually set up a lambda configuration as with a near-normal incident shock.
Approximate representations of the above cases are shown in Fig. 7.55.
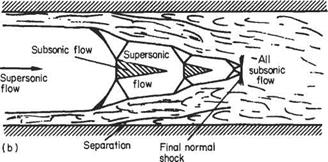
One other condition of interest that occurs in a closed uniform duct (two-dimensional or circular) when a supersonic stream is being retarded by setting up a back pressure in the duct. In the absence of boundary layers, the retardation would normally occur through a plane normal shock across the duct, reducing the flow, in one jump, from supersonic to subsonic speed. However, because of the presence of
Fig. 7.55
the boundary layer, which thickens ahead of the shock, causing the base of the shock to thicken or bifurcate (lambda shock) depending on the nature and thickness of the boundary layer, in much the same way as for the transonic single-surface case.
Because of the considerable thickening of the boundary layers, the net flow area is reduced and may reaccelerate the subsonic flow to supersonic, causing another normal shock to be set up to re-establish the subsonic condition. This situation may be repeated several times until the flow reduces to what is effectively fully-developed subsonic boundary-layer flow. If the boundary layers are initially thick, the first shock may show a large degree of bifurcation owing to the large change of flow direction well ahead of the normal part of the shock. In some cases, the extent of the normal shock may be reduced almost to zero and a diamond pattern of shocks develops in the duct. Several typical configurations of this sort are depicted in Fig. 7.56.
To sum up the last two sections, it can be stated that, in contrast to the case of most subsonic mainstream flows, interaction between the viscous boundary layer and the effectively inviscid, supersonic, mainstream flow is likely to be appreciable. In the subsonic case, unless complete separation takes place, the effect of the boundary-layer
|
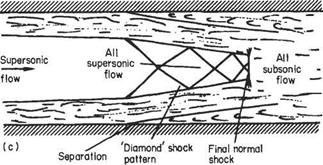
Fig. 7.56 (a) Low upstream Mach number thin boundary layer; relatively small pressure rise; no separation, (b) Higher upstream Mach number; thin boundary layer; larger overall pressure rise; separation at first shock, (c) Moderately high upstream Mach number; thick boundary layer; large overall pressure rise; separation at first shock
|
development on the mainstream can usually be neglected, so that an inviscid mainstream-flow theory can be developed independently of conditions in the boundary layer. The growth of the latter can then be investigated in terms of the velocities and streamwise pressure gradients that exist in the previously determined mainstream flow.
In the supersonic (and transonic) case, the very large pressure gradients that exist across an incident shock wave are propagated both up – and downstream in the boundary layer. The rapid thickening and possible local separation that result
|
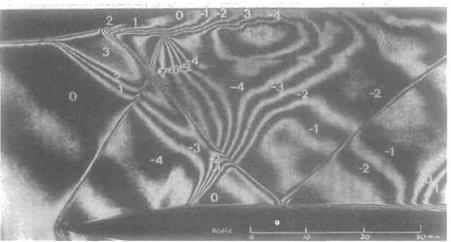
Fig. 7.57 Complex wave interactions in supersonic flow: The flow is from left to right for this holographic interferogram. Complex interactions occur between shock waves, expansion waves and boundary layers on the upper and lower walls. An oblique shock wave runs up and to the right from the leading edge of the wedge. This interacts with a fan of expansion waves running downwards and to the right from a sharp turn in the upper surface. A subsequent compression turn in the upper surface located at the top of the photograph generates a second shock wave running downward and to the right which interacts first with the leading-edge shock wave, then with an expansion wave emanating from the lower surface, and finally with the boundary layer on the lower surface. The pressure rise associated with this second shock wave has led to boundary-layer separation on the upper surface close to the label 2. See Fig. 7.55 on page 480. Interferograms can supply quantitative data in form of density or Mach number values. The Mach numbers corresponding to the numerical labels (given in parentheses) appearing in the photograph are as follows: 0.92(-7), 0.98(-6), 1.05(-5), 1.13(-4), 1.21(-3), 1.28(-2),
1.36(-1), 1.44(0), 1.53(1), 1.64(2), 1.75(3). (The photograph was taken by P. J. Bryanston-Cross in the Engineering Department, University of Warwick, UK.)
|
frequently have considerable effects on the way in which the shock is reflected by the boundary layer (see Fig. 7.57). In this way, the whole character of the mainstream flow may frequently be changed. It follows from this that a supersonic mainstream flow is much more dependent on Reynolds number than a subsonic one because of the appreciably different effects of an incident shock on laminar and turbulent boundary layers. The Reynolds number, of course, has a strong influence on the type of boundary layer that will occur. The theoretical quantitative prediction of supersonic stream behaviour in the presence of boundary layers is, consequently, extremely difficult.
Exercises
1 A thin plate of length 50 cm is held in uniform water flow such that the length of the plate is parallel to the flow direction. The flow speed is lOm/s, the viscosity, /л — 1.0 x lO-3 Pa s, and the water density is 998 kg/nr3.
(i) What is the Reynolds number based on plate length. What can be deduced from its value?
(ii) On the assumption that the boundary layer is laminar over the whole surface, use the approximate theory based on the momentum-integral equation to find:
(a) The boundary-layer thickness at the trailing edge of the plate; and
(b) The skin-friction drag coefficient.
(iii) Repeat (ii), but now assume that the boundary layer is turbulent over the whole surface. (Use the formulae derived from the 1/7-power-law velocity profile.) {Answer. Rei. = 500 000; 6 ~ 3.3 mm, C^f ~ 0.0018; 6 ~ 13.4mm, Cot ~ 0.0052)
2 A thin plate of length 1.0 m is held in a uniform air flow such that the length of the plate is parallel to the flow direction. The flow speed is 25m/s, the viscosity, jj, = 14.96 x 10-6Pas, and the air density is 1.203 kg/m3.
(i) If it is known that transition from laminar to turbulent flow occurs when the Reynolds number based on x reaches 500 000, find the transition point.
(ii) Calculate the equivalent plate length for an all-turbulent boundary layer with the same momentum thickness at the trailing edge as the actual boundary layer.
(iii) Calculate the coefficient of skin-friction drag per unit breadth for the part of the plate with
(a) A laminar boundary layer; and
(b) A turbulent boundary layer. (Use the formulae based on the 1/7-power-law velocity profile.)
(iv) Calculate the total drag per unit breadth.
(v) Estimate the percentage of drag due to the turbulent boundary layer alone.
{Answer. 300 mm from the leading edge; 782 mm; 0.00214, 0.00431;
1.44N/m per side; 88%)
3 The geometric and aerodynamic data for a wing of a large white butterfly is
as follows: Flight speed, Ux = 1.35m/s; Average chord, c = 25mm; Average span, s = 50mm; air density = 1.2kg/m3; air viscosity, ц = 18 x 10_6Pas; Drag at zero lift = 120 |j. N (measured on a miniature wind-tunnel balance). Estimate the boundary-layer thickness at the trailing edge. Also compare the measured drag with the estimated skin-friction drag. How would you account for any difference in value? {Answer. 2.5 mm; 75 pN)
4 A submarine is 130 m long and has a mean perimeter of 50 m. Assume its wetted surface area is hydraulically smooth and is equivalent to a flat plate measuring 130 m x 50 m. Calculate the power required to maintain a cruising speed of 16m/s when submerged in a polar sea at 0°C. If the engines develop the same power as before, at what speed would the submarine be able to cruise in a tropical sea at 20 °С?
Take the water density to be 1000kg/m3, and its kinematic viscosity to be 1.79 x 10-6m2/s at 0°C and 1.01 x 10-6m2/s at 20°C.
{Answer. 20.5 MW; 16.37m/s)
5 A sailing vessel is 64 m long and its hull has a wetted surface area of 560 m2. Its top speed is about 9m/s. Assume that normally the equivalent sand-grain roughness, ks, of the hull is about 0.2 mm.
The total resistance of the hull is composed of wave drag plus skin-friction drag. Assume that the latter can be estimated by assuming it to be the same as the equivalent flat plate. The skin-friction drag is exactly half the total drag when sailing at the top speed under normal conditions. Assuming that the water density and kinematic viscosity are 1000 kg/m3 and 1.2 x 10_6m2/s respectively, estimate:
(a) The admissible roughness for the vessel;
(b) The power required to maintain the vessel at its top speed when the hull is unfouled (having its original sand-grain roughness);
(c) The amount by which the vessel’s top speed would be reduced if barnacles and seaweed were allowed to remain adhered to the hull, thereby raising the equivalent sand-grain roughness, ks, to about 5 mm.
(Answer: 2.2 pm; 1.06 MW; 8.04 m/s, i. e. a reduction of 10.7%)
6 Suppose that the top surface of a light-aircraft wing travelling at an air speed of
55 m/s were assumed to be equivalent to a flat plate of length 2 m. Laminar-turbulent transition is known to occur at a distance of 0.75 m from the leading edge. Given that the kinematic viscosity of air is 15 x 10_6m2/s, estimate the coefficient of skin – friction drag. (Answer: 0.00223)
7 Dolphins have been observd to swim at sustained speeds up to 11 m/s. According to the distinguished zoologist Sir James Gray, this speed could only be achieved, assuming normal hydrodynamic conditions prevail, if the power produced per unit mass of muscle far exceeds that produced by other mammalian muscles. This result is known as Gray’s paradox. The object of this exercise is to carry out revised estimates of the power required in order to check the soundness of Gray’s calculations.
Assume that the dolphin’s body is hydrodynamically equivalent to a prolate spheroid (formed by an ellipse rotated about its major axis) of 2 m length with a maximum thickness-to-length ratio of 1:6.
4 ,
Volume of a prolate spheroid = – тгаЬ
Surface/area = 2ттЬ2 + ,_ arc sin
where 2a is the length and 2b the maximum thickness.
Calculate the dimensions of the equivalent flat plate and estimate the power required to overcome the hydrodynamic drag (assuming it to be solely due to skin friction) at 11 m/s for the following two cases:
(a) Assuming that the transitional Reynolds number takes the same value as the maximum found for a flat plate, i. e. 2 x 106, say;
(b) Assuming that transition occurs at the point of maximum thickness (i. e. at the point of minimum pressure), which is located half-way along the body.
The propulsive power is supplied by a large group of muscles arranged around the spine, typically their total mass is about 36 kg, the total mass of the dolphin being typically about 90 kg. Assuming that the propulsive efficiency of the dolphin’s tail unit is about 75%, estimate the power required per unit mass of muscle for the two cases above. Compare the results with the values given below.
Running man, 40 W/kg; Hovering humming-bird, 65 W/kg.
(Answer: 2m x 0.832m; 2.87kW, 1.75kW; 106 W/kg, 65 W/kg)
8 Many years ago the magazine The Scientific American published a letter concerned with the aerodynamics of pollen spores. A photograph accompanied the letter showing a spore having a diameter of about 20 pm and looking remarkably like a golf ball. The gist of the letter was that nature had discovered the principle of golf – ball aerodynamics millions of years before man. Explain why the letter-writer’s logic is faulty.
![]()
























 ,___ . .. waves Transition to
,___ . .. waves Transition to