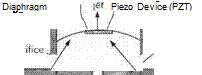
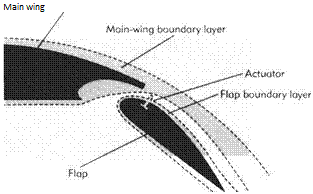
Nowadays, with the ready availability of powerful desktop computers, it is perfectly feasible to solve the boundary-layer equations computationally in their original form as partial differential equations. Consequently, methods based on the momentum integral equation are now less widely used. Computational solution of the boundary – layer equations is now a routine matter for industry and university researchers alike, and suitable computer programs are widely available. Nevertheless, specialized numerical techniques are necessary and difficulties are commonly encountered. Good expositions of the required techniques and the pitfalls to be avoided are available in several textbooks.[49] All-purpose commercial software packages for computational fluid dynamics are also widely available. As a general rule such software does not handle boundary layers well owing to the fine resolution required near the wall*. Only a brief introduction to the computational methods used for boundary layers will be given here. For full details the recommended texts should be consulted.
It is clear from the examples given that in aeronautical applications boundary layers are typically very thin compared with the streamwise dimensions of a body like a wing. This in itself would pose difficulties for computational solution. For this reason equations (7.7) and (7.14) are usually used in the following non-dimensional form
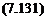
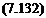 dU 9V_ dX + dY~
dU 9V_ dX + dY~
dU dU _ dP &U UdX+VdY~ d X +dY2
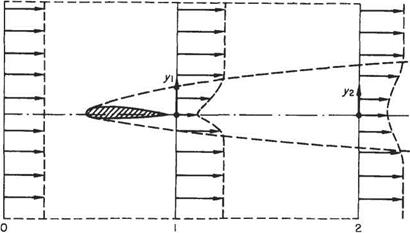
where U = u/Urc, V = v/iRebUoo), P — p/(pU£.), X = x/L, and Y = y/(LReL). In many respects this form was suggested by the method of derivation given in Section 7.3.1. What this form of the equations achieves is to make the effective range of both independent variables X and Y similar in size, i. e. 0(1). The two dependent variables U and V are also both 0(1). Thus the grid used to discretize the equations for computational solution can be taken as rectangular and rectilinear, as depicted in Fig. 7.47.
Mathematically, the boundary-layer equations are what are termed parabolic. What this means for computational purposes is that one starts at some initial point X = Xq, say, where U is known as a function of Y, e. g. the stagnation-point solution (see Section 2.10.3) should be used in the vicinity of the fore stagnation point. The object of the computational scheme is then to compute the solution at Xq + AX where AX is a small step around the body surface. One then repeats this procedure until the trailing edge or the boundary-layer separation point is reached. For obvious
Fig. 7.47 reasons such a procedure is called a marching scheme. The fact that the equations are parabolic allows one to use such a marching scheme. It would not work for the Laplace equation, for example. In this case, quite different methods must be used (see Section 3.5).
The simplest approach is based on a so-called explicit finite-difference scheme. This will be briefly explained below.
It is assumed that the values of V are known along the line X — Xt, i. e. the discrete values at the grid points (like P) are known. The object is to devise a scheme for calculating the values of U at the grid points along X = T,+1. To do this we rewrite Eqn (7.132) in a form for determining dU/dX at the point P in Fig. 7.47. Thus
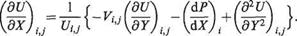 (7.133)
(7.133)
Values at X = Xi+ can then be estimated by writing
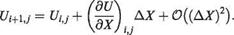 (7.134)
(7.134)
The last term on the right-hand side indicates the size of the error involved in using this approximation. The pressure gradient term in Eqn (7.133) is a known function of X obtained either from experimental data or from the solution for the potential flow around the body. But the other terms have to be estimated using finite differences. To obtain estimates for the first and second derivatives with respect to Y we start with Taylor expansions about the point P in the positive and negative Y directions. Thus we obtain
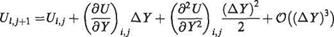
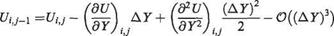
(7.135a)
(7.135b)
Viscous flow and boundaiy layers 461
<7Л36>
We then add Eqns (7.135a) and (7.135b) and rearrange to obtain the estimate
(0),= Uw’ U‘J~’+ °((Ar)i>- <7Л37)
The results given in Eqns (7.136) and (7.137) are usually referred as centred finite differences. Finally, the value of Vjj also has to be estimated. This has to be obtained from Eqn (7.131) which can be rewritten as
There are two problems with this result. First it gives V, j+i rather than V,-,/, this is easily remedied by replacing j by j — 1 to obtain
The other problem is that it requires a value of (dU/dX)j j_l. But the very reason we needed to estimate Vtj in the first place was to obtain an estimate for (dU/dX)jj Fortunately, this does not represent a problem provided the calculations are done in the right order.
At the wall, say j = 0, U = V = 0 (assuming it to be impermeable), also from the continuity equation (7.131), dV/dY = 0. Thus, using an equation analogous to Eqn (7.135a),
With this estimate of F,- i, (dU/dX),■ j can now be estimated from Eqn (7.133), the first term on the right-hand side being equivalently zero. Ui+1, i is then estimated from Eqn (7.134). All the values are now known for j = 1. The next step is to set j = 2 in Eqn (7.138), so that
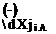 Vt,2 = V, о -2AY
Vt,2 = V, о -2AY
=o
(dU/dX)j 2 can now be estimated from Eqn (7.133) and so on right across the boundary layer. It is necessary, of course, to choose an upper boundary to the computational domain at a finite, but suitably large, height, у = Yj, corresponding to j = J, say.
This explicit finite-difference scheme is relatively simple to execute. But explicit schemes are far from ideal for boundary-layer calculations. Their main drawback is
that their use leads to numerical instability that is characterized by the solution displaying increasingly large oscillations as the calculation marches downstream leading to unacceptedly large errors. In order to ensure that this does not happen, it is necessary to impose the following condition on the streamwise step length in order to ensure numerical stability:
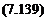 ДЛГ<і|тіп(С/і;;.)(ДУ)2
ДЛГ<і|тіп(С/і;;.)(ДУ)2
Since U is very small at the first grid point near the wall, very small values of AX will be required to ensure numerical stability.
Because of the problems with numerical instability, so-called implicit schemes are much to be preferred, because these permit step-size to be determined by considerations of accuracy rather than numerical stability. Here a scheme based on the Crank – Nicholson method will be briefly described. The essential idea is to rewrite Eqn
(7.134) 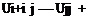
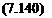
in the form
So that the derivative at x = x,- is replaced by the average of that and the derivative at x = x,_i. Formally, this is more accurate and numerically much more stable. The problem is that Eqn (7.133) implies that
and Eqns (7.136) and (7.137) imply that
Thus the unknown values of U at У,_ь i. e. Ui+j(j = 1,…,/), appear on both sides of Eqn (7.140). This is what is meant by the term implicit. In order to solve Eqn (7.140) for these unknowns it must be rearranged as a matrix equation of the form
AU = R
where A is the coefficient matrix, U is a column matrix containing the unknowns UiM. jti = 1, ■ ■ ■, J), and R is a column matrix of containing known quantities. Fortunately A has a tridiagonal form, i. e. only the main diagonal and the two diagonals either side of it are non-zero. Tridiagonal matrix equations can be solved very efficiently using the Thomas (or Tridiagonal) algorithm, versions of which can be found in Press et al. (loc. cit.) and on the Internet site associated with Ferziger (1998) {loc. cit.).
One of the most popular and widely used implicit schemes for computational solution of the boundary-layer equations is the Keller[50] box scheme which is slightly more accurate than the Crank-Nicholson method.
![]()











 (7.161)
(7.161)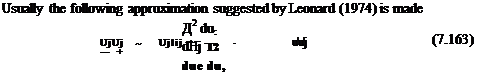
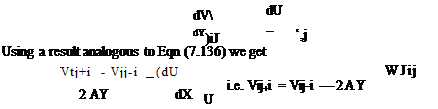
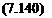
 а л 3 , Л2 4 /37 Л A2 Е2(Л) -4 + т-—Л + — + —( — – — – —
а л 3 , Л2 4 /37 Л A2 Е2(Л) -4 + т-—Л + — + —( — – — – —