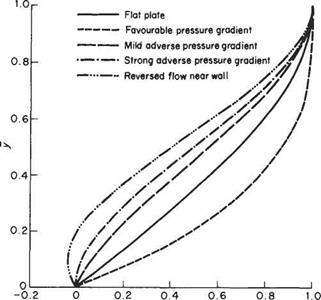
Flow past cylinders and spheres
Some of the properties of boundary layers discussed above help in the explanation of the behaviour, under certain conditions, of a cylinder or sphere immersed in a uniform free stream. So far discussion has been restricted to the flow over bodies of reasonably streamline form, behind which a relatively thin wake is formed. In such cases, the drag forces are largely due to surface friction, i. e. to shear stresses at the base of the boundary layer. When dealing with non-streamlined or bluff bodies, it is found that, because of the adverse effect of a positive pressure gradient on the boundary layer, the flow usually separates somewhere near points at the maximum cross-section, with the formation of a broad wake. As a result, the skin-friction drag is only small, and the major part of the total drag now consists of form drag due to the large area at the rear of the body acted upon by a reduced pressure in the wake region. Experimental observation of the flow past a sphere or cylinder indicates that the drag of the body is markedly influenced by the crosssectional area of the wake, a broad wake being accompanied by a relatively high drag and vice versa.
The way in which the flow pattern around a bluff body can change dramatically as the Reynolds number is varied may be considered with reference to the flow past a circular cylinder. For the most part the flow past a sphere also behaves in a similar way. At very low Reynolds number,* i. e. less than unity, the flow behaves as if it were purely viscous with negligible inertia. Such flow is known as creeping or Stokes flow. For such flows there are no boundary layers and the effects of viscosity extend an infinite distance from the body. The streamlines are completely symmetrical fore and aft, as depicted in Fig. 7.15a. In appearance the streamline pattern is superficially similar to that for potential flow. For creeping flow, however, the influence of the cylinder on the streamlines extend to much greater distances than for potential flow. Skin-friction drag is the only force generated by the fluid flow on the cylinder. Consequently, the body with the lowest drag for a fixed volume is the sphere.
|
|
|
|
|
|
|
|

Perhaps, it is for this reason that microscopic swimmers such as protozoa, bacteria and spermatazoa tend to be near-spherical. In the range 1 < Re < 5, the streamline pattern remains fairly similar to that of Fig. 7.15a, except that as Re is increased within this range a more and more pronounced asymmetry develops between the fore and aft directions. Nevertheless, the flow remains attached.
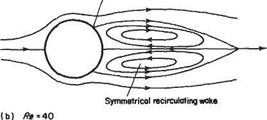
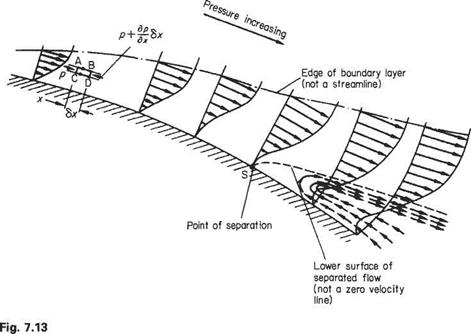
When Re exceeds a value of about 5, a much more profound change in the flow pattern occurs. The flow separates from the cylinder surface to form a closed wake of recirculating flow – see Fig. 7.15b. The wake grows progressively in length as Re is increased from 5 up to about 41. The flow pattern is symmetrical about the horizontal axis and is steady, i. e. it does not change with time. At these comparatively low Reynolds numbers the effects of viscosity still extend a considerable distance from the surface, so it is not valid to use the concept of the boundary layer, nevertheless the explanation for flow separation occurring is substantially the same as that given in Section 7.4.
When Re exceeds a value of about 41 another profound change occurs; steady flow becomes impossible. In some respects what happens is similar to the early stages of laminar-turbulent transition (see Section 7.9), in that the steady recirculating wake flow, seen in Fig. 7.15b, becomes unstable to small disturbances. In this case, though, the small disturbances develop as vortices rather than waves. Also in this case, the small disturbances do not develop into turbulent flow, but rather a steady laminar wake develops into an unsteady, but stable, laminar wake. The vortices are generated
|
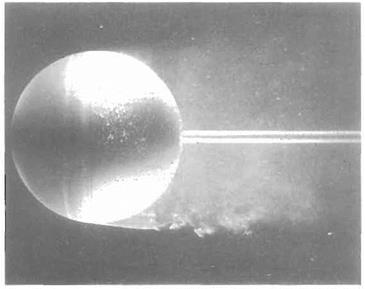
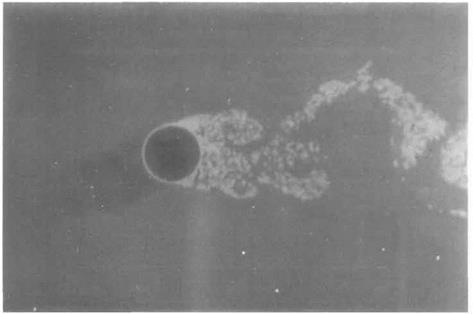
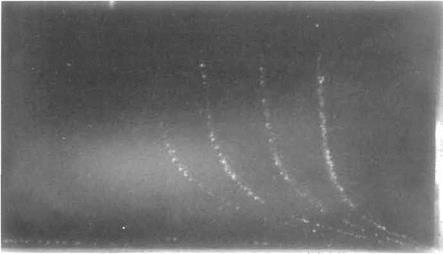
Fig. 7.16 The wake of a circular cylinder at Reo ~ 5000: Vortices are formed when flow passes over circular cylinders for a wide range of Reynolds numbers – see Fig. 7.15 on page 400. The flow is from left to right. The Reynolds number is sufficiently large for a thin laminar boundary layer to form over the upstream surface of the cylinder. It separates at a point just ahead of maximum thickness and breaks up into a turbulent wake which is dominated by large-scale vortices. Flow visualization is obtained by using aluminium particle tracers on water flow. [The photograph was taken by D. J. Buckingham at the School of Engineering, University of Exeter, UK.) |
periodically on alternate sides of the horizontal axis through the wake and the centre of the cylinder. In this way, a row of vortices are formed, similar to that shown in Fig. 7.17c. The vortex row persists for a very considerable distance downstream. This phenomenon was first explained theoretically by von Karman in the first decade of the twentieth century.
 |
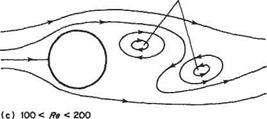
For Reynolds numbers between just above 40 and about 100 the vortex street develops from amplified disturbances in the wake. However, as the Reynolds number
rises an identifiable thin boundary layer begins to form on the cylinder surface and the disturbance develops increasingly closer to the cylinder. Finally, above about Re = 100 eddies are shed alternately from the laminar separation points on either side of the cylinder (see Fig. 7.16). Thus, a vortex will be generated in the region behind the separation point on one side, while a corresponding vortex on the other side will break away from the cylinder and move downstream in the wake. When the attached vortex reaches a particular strength, it will in turn break away and a new vortex will begin to develop again on the second side and so on.
The wake thus consists of a procession of equal-strength vortices, equally spaced but alternating in sign. This type of wake, which can occur behind all long cylinders of bluff cross-section, including flat plates normal to the flow direction, is termed a von Karman vortex street or trail (see Fig. 7.17a). In a uniform stream flowing past a cylinder the vortices move downstream at a speed somewhat less than the free – stream velocity, the reduction in speed being inversely proportional to the streamwise distance separating alternate vortices.
It will be appreciated that, during the formation of any single vortex while it is bound to the cylinder, an increasing circulation will exist about the cylinder, with the consequent generation of a transverse (lift) force. With the development of each successive vortex this force will change sign, giving rise to an alternating transverse force on the cylinder at the same frequency as the vortex shedding. If the frequency happens to coincide with the natural frequency of oscillation of the cylinder, however it may be supported, then appreciable vibration may be caused. This phenomenon is responsible, for example, for the singing of telegraph wires in the wind (Aeolian tones).
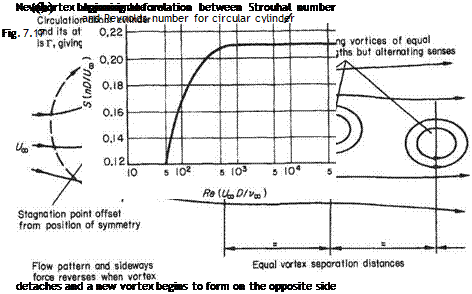
A unique relationship is found to exist between the Reynolds number and a dimensionless parameter involving the shedding frequency. This parameter, known as the Strouhal number, is defined by the expression S = nDjUoo, where n is the frequency of vortex shedding. Figure 7.17b shows the typical variation of 5 with Re in the vortex street range.
Despite the many other changes, described below, which occur in the flow pattern as Re increases still further, markedly periodic vortex shedding remains a characteristic flow around the circular cylinder and other bluff bodies up to the highest Reynolds numbers. This phenomenon can have important consequences in engineering applications. An example was the Tacoma Narrows Bridge (in Washington State, U. S.A.) A natural frequency of the bridge deck was close to its shedding frequency causing resonant behaviour in moderate winds, although its collapse in 1940 was due to torsional aeroelastic instability excited by stronger winds.
For two ranges of Reynolds number, namely 200 < Re < 400 and 3 x 105 < Re < 3 x 106, the regularity of vortex shedding is greatly diminished. In the former range very considerable scatter occurs in values of Strouhal number, while for the latter range all periodicity disappears except very close to the cylinder. The values of Reynolds number marking the limits of these two ranges are associated with pronounced changes in the flow pattern. In the case of Re ~ 400 and 3 x 106 the transitions in flow pattern are such as to restore periodicity.
Below Re ~ 200 the vortex street persists to great distances downstream. Above this Reynolds number, transition to turbulent flow occurs in the wake thereby destroying the periodic vortex wake far downstream. At this Reynolds number the vortex street also becomes unstable to three-dimensional disturbances leading to greater irregularity.
At Re ~ 400 a further change occurs. Transition to turbulence now occurs close to the separation points on the cylinder. Rather curiously, perhaps, this has a stabilizing
|
|
|
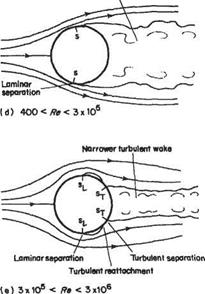
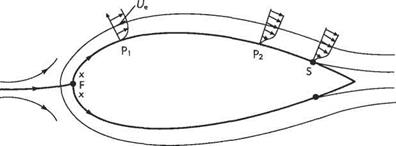
effect on the shedding frequency even though the vortices themselves develop considerable irregular fluctuations. This pattern with laminar boundary-layer separation and a turbulent vortex wake persists until Re ~ 3 x 10s, and is illustrated in Figs 7.15d and 7.16. Note that with laminar separation the flow separates at points on the front half of the cylinder, thereby forming a large wake and producing a high-level of form drag. In this case, the contribution of skin-friction drag is all but negligible.
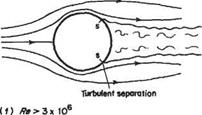
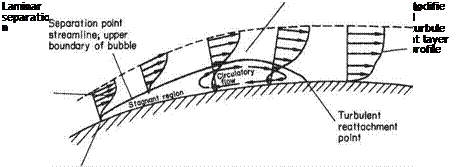
When the Reynolds number reaches a value in the vicinity of 3 x 10s the laminar boundary layer undergoes transition to turbulence almost immediately after separation. The increased mixing re-energizes the separated flow causing it to reattach as a turbulent boundary layer, thereby forming a separation bubble (as described in Section 7.4.1) – see Figs 7.15e and 7.18.
At this critical stage the second and final point of separation, which now takes place in a turbulent layer, moves suddenly downstream, because of the better sticking property of the turbulent layer, and the wake width is very appreciably decreased. This stage is therefore accompanied by a sudden decrease in the total drag of the cylinder. For this reason the value of Re at which this transition in flow pattern occurs is often called the Critical Reynolds number. The wake vorticity remains random with no clearly discernible frequency. With further increase in Reynolds number the wake width will gradually increase to begin with, as the turbulent separation points slowly move upstream round the rear surface. The total drag continues to increase steadily in this stage, due to increases in both pressure and skin-friction drag, although the drag coefficient, defined by
![]() drag per unit span
drag per unit span
{PooUlD tends to become constant, at about 0.6, for values of Re > 1.3 x 106. The final change in the flow pattern occurs at Re ~ 3 x 106 when the separation bubble disappears, see Fig. 7.15f. This transition has a stabilizing effect on the shedding frequency which becomes discernible again. Си rises slowly as the Reynolds number increases beyond 3 x 106.
The actual value of the Reynolds number at the critical stage when the dramatic drag decrease occurs depends, for a smooth cylinder, on the small-scale turbulence level existing in the oncoming free stream (see Fig. 7.18). Increased turbulence, or, alternatively, increased surface roughness, will provoke turbulent reattachment, with its accompanying drag decrease, at a lower Reynolds number. The behaviour of a smooth sphere under similarly varying conditions exhibits the same characteristics as the cylinder, although the Reynolds numbers corresponding to the changes of flow regime are somewhat different. One marked difference in behaviour is that the eddying vortex street, typical of bluff cylinders, does not develop in so regular a fashion behind a sphere. Graphs showing the variations of drag coefficient with Reynolds number for circular cylinders and spheres are given in Fig. 7.19.













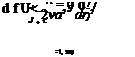
 Uaо….
Uaо….
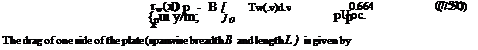
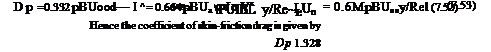
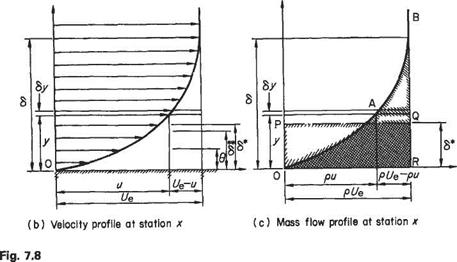
 dy
dy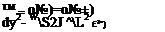 cPu
cPu