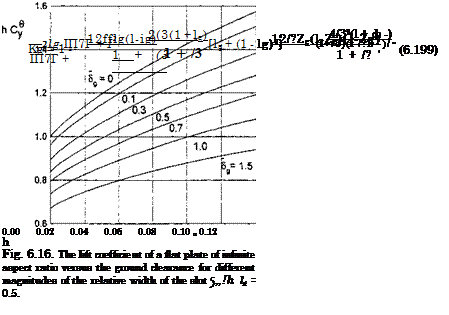
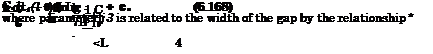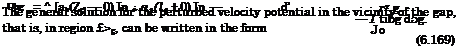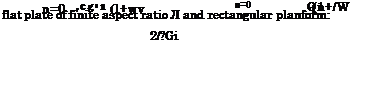The aperiodic behavior of aerodynamic characteristics versus time can result from aperiodic motions of the lifting surface (takeoff, landing, acceleration – decceleration, the variation of cruise parameters due to the action of control surfaces) and also due to aperiodic perturbations, caused by unevenness of the ground or gusts. If the problem is linearized with respect to the perturbations, then the Fourier integral transform method can be used for the analysis of the response of the lifting system to the aperiodic perturbation or motion. In what follows, the analysis will be restricted to the aerodynamics of a lifting surface in the ground effect under the action of aperiodic perturbations (irregularities or steps on the ground or gusts). The solutions of the problems of motion of the wing in close proximity to a wavy sinusoidal wall or under the action of a vertical sinusoidal gust for arbitrary Strouhal numbers can be used as transfer functions for the application of the Fourier integral.
It is well known that if a stable system that has behavior described by a linear differential equation with linear boundary conditions is subject to the prolonged action of harmonic perturbation, then the response of the system will change in time harmonically and with the same frequency. Consequently, within the linear theory, the aerodynamic characteristics due to harmonic perturbation, say the lift coefficient CVe(t), can be written as
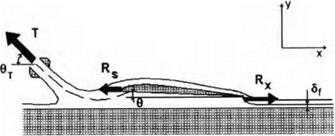
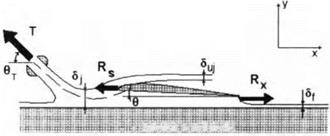
CVe(t) — eGy(k)exp(ikt),
where Gy(k) is a complex transfer function of the lift coefficient and є is the amplitude of the kinematic parameter, characterizing the harmonic perturbation. For example, when a wing is subject to the action of regular waves on the ground surface, the parameter є can be set equal to the wave amplitude aw, whereas for a vertical harmonic gust, є can be equated to the maximum velocity in the gust ug, к is the Strouhal number, corresponding to the perturbation under consideration, and і = is an imaginary unit. Transfer functions of moment coefficients can be introduced in a similar manner. We consider a lifting surface, moving at a constant speed and without slipping, in close proximity to the ground and subject to action of aperiodic perturbations such as an arbitrary irregularity on the ground or a vertical gust of arbitrary form. For simplification, assume that motion of the wing takes place in a direction perpendicular to the front of the perturbation. Assume also that the speed of the perturbation is negligiably small compared to the speed of the lifting surface,[40] so that the waves can be viewed as still with respect to the wing. Introduce a fixed coordinate system хі, г/і, and z in which the directions of all axes coincide with those of the moving coordinate system x,2/, 2, introduced earlier. Planes xOzi and хОу coincide with unperturbed position of the ground plane and the plane of symmetry of the wing, respectively. Let the perturbation have the following form in a fixed coordinate system:
V{xi) = Є/ОEl),
where again є is a parameter that characterizes the magnitude of the per – turbatiOon, for example, the relative (in terms of the root chord) height of an irregularity on the ground surface, and f(xi) is a function of the order of 0(1) describing the form of the perturbation. Let the form function of the perturbation be absolutely integrable on the interval — oo < x < oo, that is,
oo
f{xidxi < oo.
-oo
Then, in a wide class of piecewise continuous functions, f(xi) is representable by the Fourier integral, see, for example, Smirnov [150]:
1 f°°
f(xx) = — Q(k) exp(ifcxi) dfc, (7.52)
27Г /_nn
where
ос Q
/(xi) exp(—ifcxi) dxi, k=—~. (7.53)
-oo Uo
The function f2(k) is a Fourier transform of the function f(xi) and conversely. Counting time from the moment t0, when the leading edge of the root chord is located just above the frontline of the perturbation and passing over to the moving coordinate system,
є r°°
V(x, t) = — Q{k) exp[ifc(x +1)] dk. (7-54)
2тг 7-ос
It follows from consideration of expression (7.54) that in the coordinate system, attached to the wing, the function V can be viewed as the result of the superposition of harmonic perturbations of the traveling wave type and the quantity єП(к)/2іг represents the amplitude of a harmonic of relative frequency k. Knowing the transfer function, i. e., the aerodynamic response of a lifting system to the action of a traveling wave of perturbation of arbitrary frequency and unit amplitude, it is easy to derive the following expressions for the coefficients of the unsteady lift and the moment upon a wing which is subject to the action of a perturbation of arbitrary form f(xi):
|
E
Cy(t) = — Gyfi(k)exp(ikt)dk7 2ТГ 7-ос
|
(7.55)
|
|
є
mz{t) — 77“ GrrizQ(k) exp(ifct) dfc,
2^ 7 — 00
|
(7.56)
|
where Gy and Grriz are complex transfer functions of the lift and the moment coefficients. As seen from (7.55) and (7.56), to determine the transient aerodynamic characteristics of a wing subject to the action of an irregular perturbation of a given form, we have to calculate the Fourier amplitudes
ад.
We find the form of the function i?(fc) for perturbations of simple shape. According to (7.53), the amplitude of the harmonic of relative frequency к can be written in a complex form
oo
f(xi) exp(—ikxi) dxi = !?i(fc) + ii?2(&)* (7.57)
-oo
For an “even” perturbation, /(—x) = f(xi),xi Є [—Z/P, LP], and
roo rLp/2
Q(k) = f2(k) = 2 f(xi) cos kxdx = 2 f{xi) cos kxi daq,
Jo Jo
(7.58)
where Lp is the length of the perturbation. For an “odd” perturbation, f{xl) = – f(-xi),xi Є [—Lp, Lp], and
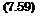 pL p/2
pL p/2
Q(k) = il?2(fc) = -2i f{xi) sinfcxi dxi
Jo
As examples of “even” perturbation consider
• cosine perturbation, defined as
, . _ Jcos(7TXi/Lp) for |жі| < Lp/2,
0 for |xi| >Lp/2.
Integration gives the Fourier amplitude in the form
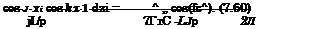 ад = 2 [
ад = 2 [
Jo
triangular perturbation, given by the function
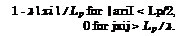
f(xi) -■
As an example of an “odd” perturbation, consider a sine-type perturbation of the form
_ f sin(27TXi/Lp) for xI < Lp/2,
0 for |xi|> Lp/2.
Calculation of the Fourier amplitudes in this case results in
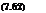 Q{k) = Ш2{к) = sin (k^-).
Q{k) = Ш2{к) = sin (k^-).
Besides the “even” and “odd” forms considered above, it is interesting to consider a step-type perturbation. The form of such perturbation is described by a Heaviside step function
Representation of the step function by the Fourier integral is known to have the form
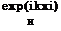
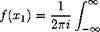 dfc,
dfc,
wherefrom ш
П(к) = іП2 = – т – (7-63)
к
Before one performs calculations for concrete cases of irregularities on the ground or vertical gusts, the origin of the fixed coordinate system should be shifted to the front of the perturbation and the transform Q{k) rewritten accordingly:
f2*(k) = fi(k) exp(ifc^),
where f2*(k) is the amplitude of a harmonic in the new coordinate system. Separating the real part of the expression for the transient lift coefficient, we obtain the expression
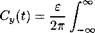 ?k{Gy(k)Q(k) exp[ifc(£ + Lp/2)]} dk. (7.64)
?k{Gy(k)Q(k) exp[ifc(£ + Lp/2)]} dk. (7.64)
Taking into account the preceding results for the unsteady lift coefficient of a wing in motion over wavy ground obtained in paragraph 7.1, we can write the lift coefficient transfer function in the form
Gy(k) = ^[A(k)-iB(k)}, (7.65)
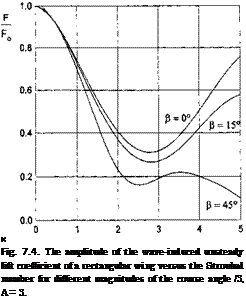
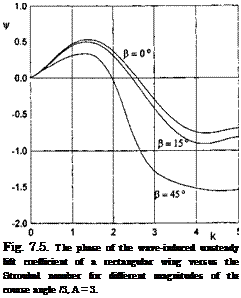
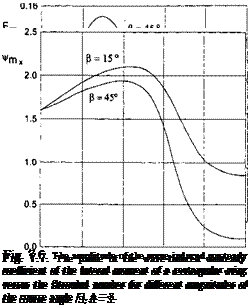
where for a rectangular wing, the parameters A(k) and B(k) depend on the Strouhal number and the aspect ratio and are determined by using the previous analysis of the aerodynamics of a wing in motion above the waves. For example, for a wing of infinite aspect ratio advancing in close proximity to sinusoidal wavy ground, the formulas for A(k) and B(k) are
A — A cos к — B sin fc, В = A sin к + Bi cos fc,
where
Ai = 2^-—^~) ~ i + k2 ^sin^ + ^ ~ ^2)cosfc ~ i];
Bi = ^ _ l) + jTjTpK1 _ k2) sinfc + fc(l – 2cosfc)].
Denoting the height of the irregularity on the ground as Oh and employing the wave amplitude aw as є, we can rewrite (7.37) as
CM) = [ (n1{k)A(k)cos{kt + ^) + B{k)sm{kt
|
—i?2 (k) A(k) sin(kt + —^) — В (к) cos(kt + j dfc, (7.66) so that in concrete cases
• for an “even” irregularity Q{k) = i? i(fc), і?2(&) = 0,
Cy(t) = Яі(*) [Л(к) cos (kt + ^) + B(k) sin (kt +
• for an “odd” irregularity Q(k) = ii?2(fc), f2i(k) = 0,
■’)
|
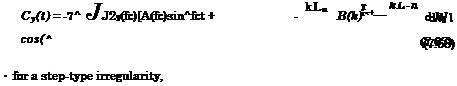
2-їїп J_00 L L 2
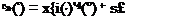 A(k) Л(°) sin kt _ Ш1 cos jfetj dk },
A(k) Л(°) sin kt _ Ш1 cos jfetj dk },
where 1(£) is a Heaviside step function, defined as
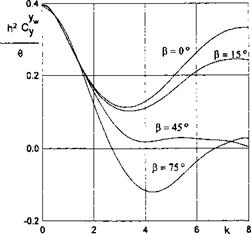
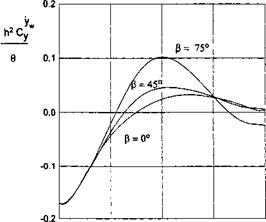
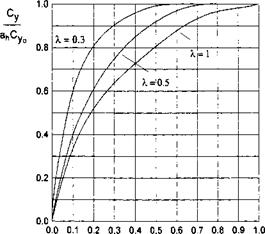
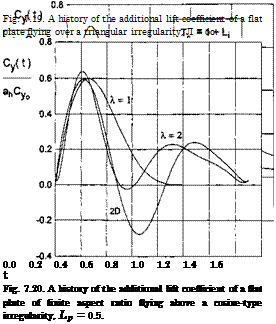
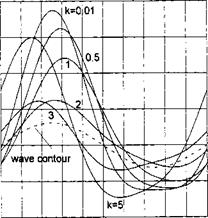
Some results of the calculations of the transient lift coefficient of a rectangular wing in motion above different types of uneven ground are presented in Figs. 7.19 and 7.20.
The vertical coordinate of each graph stands for Cy{t) /а^Суо, where Cy0 is a steady-state (cruise) lift coefficient of a flat rectangular wing in the ground effect and аь = ah/h is characteristic vertical dimension of the irregularity related to the ground clearance.
|
t
Fig. 7.21. A history of the additional lift coefficient of a rectangular wing of finite aspect ratio, flying over a “step” in the extreme ground effect.
|
An analysis of calculated data for an isolated irregularity shows that
• for wings of small-aspect ratio at initial moments, the additional lift first increases, then drops and tends to zero. In some cases the influence of the perturbation vanishes before the trailing edge of the wing finds itself beyond the irregularity;
• with an increase of the aspect ratio, the character of the curves changes somewhat. After the first maximum of additional lift, the second one appears, which is smaller in size. The influence of the perturbation may be observed longer than it takes for the wing to overfly the irregularity completely. For short convex local deformations of the ground and for certain time periods, negative magnitudes of additional lift due to the perturbation may appear;
• the magnitude of the maximal additional force due to the local irregularity increases with an increase in the amplitude of the irregularity and the aspect ratio and with a decrease of the relative ground clearance measured between the trailing edge and the unperturbed ground plane.
The data presented in Fig. 7.21 characterize the variation in time of the additional lift force for a step type irregularity.
It follows from Fig. 7.21 that with a decrease in the aspect ratio, the transition to the steady state takes place faster.
Conclusions formulated for flight above an irregularity on the ground generally remain valid when the wing is subject to the action of vertical aperiodic gust Presented here are only the results associated with the influence of the so-called step gust. In the case of a step gust the function that characterizes the distribution of the vertical velocities in the gust has the form of a
Heaviside step function
For this case, as shown earlier, the Fourier amplitude function takes the form described by equation (7.63). For an infinite aspect ratio Л = oo, the expression for the transient lift coefficient of a wing under the action of a vertical step gust can be derived in an analytical form. It can be shown that for A = oo, the corresponding complex transfer functions of the lift and the moment coefficients are given by
Taking into account (7.69) the expressions for the coefficients of transient lift and the moment coefficients for a wing of infinite aspect ratio under the action of a vertical step gust will be
|
– Vg0 [l(f) 1 f°° (k sinkt +cos kt) d/ j
Hi 7Г У—oq 1 + № –
|
|
|
— ^—-[l — exp(—t)] for t > 0;
|
(7.70)
|
|
2 у
mz — -^[1 – exp(-£)] for t > 0,
|
(7.71)
|
where 1 (t) is a Heaviside function.
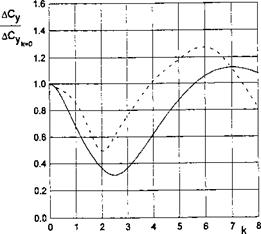
It is remarkable that for the case under consideration, the point of the application of the additional lift force due to the gust remains at the same time-independent position, namely, at a distance of one-third of the chord length from the leading edge. Some results of the calculations, carried out with help of formula (7.70) for A = oo and by numerical integration for rectangular wings of a finite aspect ratio, are presented in Fig. 7.22.
This figure features the dependence on time of the ratio Cy(t)/СУоо, where СУоо is a steady-state magnitude of the lift coefficient. In the same figure, the dashed lines designate similar results for an unbounded fluid obtained analytically by Kussner [152] for a wing of infinite aspect ratio (see Bisplinghoff et al. [151]) and numerically by the method of discrete vortices; see Belot – serkovsky [139]. A comparison of the results for the two limiting cases of the extreme ground effect (h 1) and an unbounded fluid (h = oo) shows that
for wings with small and medium aspect ratios, corresponding variations of the transient lift are steeper near the ground compared to the out-of-ground effect.
At the same time, comparison with calculations of Kussner demonstrates that for wings of very large aspect ratios transition to a steady state also occurs faster, although at the initial period of time, the curve of the transient lift coefficient goes upward more steeply for an infinite fluid.

|
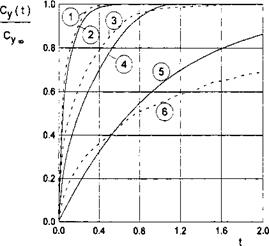
Fig. 7.22. A time history of the lift coefficient of a rectangular wing of finite aspect ratio under the action of a “step”-type vertical gust (solid lines: present theory for h <C 1; 2: Л = 0.3; 4: A = 1; 5: A = oo; dashed lines: calculated results for h = oo; 1: A = 0.25; and 3: A = 1 (from Belotserkovsky [139]); and 6: A = oo (from Kiissner [152]).
|
|
![]() 1-х
1-х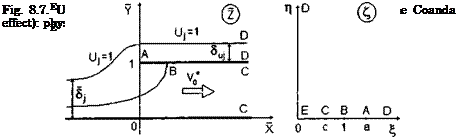
 d w л a — 1 1
d w л a — 1 1![]() (a+ 1)2
(a+ 1)2![]() a2 + 4a – 1
a2 + 4a – 1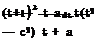
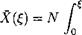 where
where










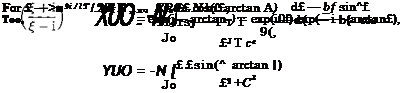
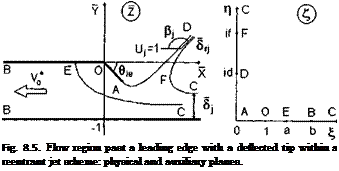
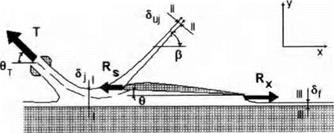
![Подпись: The unknown constants are determined from the following conditions: 1 / dw TTN a2+ d2 = ~ 2i Jid dC _ 2 b2 + d2 ~ rJ’ (8.22) 1 f dw nN b2 — a2 ~ 2i Л dC ^ “ 2 b2 + d2 ~ V°' (8.23) It follows from the condition of mass conservation that Qc = QB + QD, Qc = Sy (8.23a) Therefrom ■= „ _ irN = QB + QD = — (8.24) and, in addition, x b2 + d? * 5> 62 — a2 V°’ (8.25) because ^(id) = ехр[-(тг - /3j)i] = - exp(i/?j), (8.25a) — arctan d + arctan — = ^le ——, 7Г a 2 (8.26) and * dw/l4 b — a/b— Іч^іе/тг V° = iZm = b + aU + l) ' (8.27) The velocity v* is determined by matching with the channel flow, for example, with a solution of equation (4.95). Because ZA = bef exp(—іве) and а N = —28-Jit, there is one more equation](/img/3131/image904.gif)
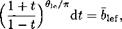 (8.28)
(8.28)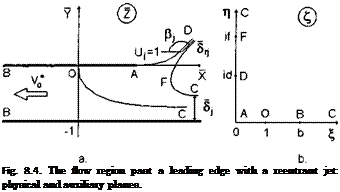
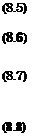


 ! – к ІІиШИІІІІІ ІмШШІІІИЯ
! – к ІІиШИІІІІІ ІмШШІІІИЯ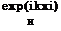
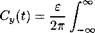 ?k{Gy(k)Q(k) exp[ifc(£ + Lp/2)]} dk. (7.64)
?k{Gy(k)Q(k) exp[ifc(£ + Lp/2)]} dk. (7.64)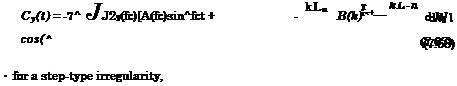


 016
016
 ~ cos 2 к 1 . 7 /7 m 1
~ cos 2 к 1 . 7 /7 m 1