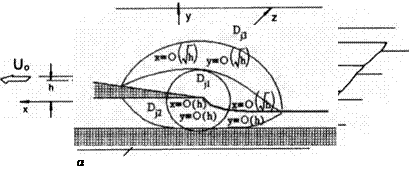
. Steady Flow Past a Jet-Flapped Wing of Finite Span
If perturbations in the flow are small, we can apply the linear theory to obtain some useful practical results. Linearization admits separate investigation of the effects of angle of pitch, curvature, and the jet flap. Therefore, when considering the flow problem for a flat wing with a jet flap, it is sufficient to treat a flat jet-flapped plate at zero incidence. Within the approximation of very small ground clearances, the flow problem is described by relationships derived from the general formulas of the theory developed in section 2. The equation is
Qx2 Qz2 = Z) ^ (6.100)
The boundary conditions are
(f = 0 at the leading and side edges (6.101)
and
![Подпись: У] = 1 - T](/img/3131/image721.gif)
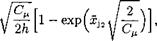
It follows from the more general nonlinear jet description that for small perturbations, the equation of the jet becomes
The jet becomes horizontal far from the trailing edge, and its ordinate far downstream is given by
a. = x = 1^ = 1-T’V% (6104)
It follows from expressions (6.105) and (6.106) that within the small perturbation theory, the form of the jet behind the trailing edge is exponential. The jet becomes horizontal at distances of the order of О(y/h) from the point of blowing. Note that due to the dependence of r and on the spanwise coordinate the magnitude of y]oo also depends on z. We consider a particular case of a rectangular wing of aspect ratio Л with a jet flap in the extreme ground effect. We let the jet have an arbitrary spanwise distribution of the momentum coefficient C^(z) and jet blowing angle r{z). Note that we can rather speak about a given spanwise distribution of the quantity (z) = t(z) yJC^{z)/2h = KjQJCj(z). The solution of the lowest order
|
CI*(Z)T(Z) dz- |
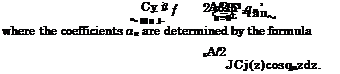 |
|
Note that these formulas do not include the reactive vertical and horizontal components of the force due to the jet momentum. For example, the reactive component of the lift coefficient can be calculated by using the formula
When considering the horizontal projection of the balance of forces acting upon the wing, we have to account for the reactive thrust of the jet. Within the frame of linear theory, the latter is equal to the coefficient Cj of the total jet momentum. In the particular case of uniform distribution of the jet momentum and the jet blowing angle = Cj = const., r(z) = r = const., the formulas (6.108)—(6.111) yield
|
16 fcj" ^ tanh qn ,3 . n=0 ™ |
(6.114) |
|
16 / Cj tanh qn tanh(gn/2) A2rV2ft^ Q4 ’ |
(6.115) |
|
4r2Cj ^ tanh2 <?„ X1 ~ A2 ^ ql ’ n=0 |
(6.116) |
|
4r2Cj 1 s A* ^0^cosh2gn- |
(6.117) |
For not very large aspect ratios, one can truncate the series to one term, that
|
16A2 [а 7Г 7Г mz ~——— t-т — tanh — tanh —, 7Г4 V 2h A 2A 4т2Сі 2 ^ ^TT4 ^,2 Cr. = 7Г1 tanh2 – = ^гттгС2, |
is,
4t2Cj
![]()
![]() 7Г2 cosh(7r/A) ’
7Г2 cosh(7r/A) ’
An important conclusion about the approximate equality of effective aspect ratios for a wing with and without a jet flap follows immediately from comparison of expressions (6.121) and (3.70). It means that the influence of the relative ground clearance on the effective aspect ratio is the same no matter how the lift is generated, by a jet flap at zero angle of pitch or by the angle of pitch without jet flap. Passing to the limit A -» oo in (6.114)—(6.117), one obtains corresponding results for two-dimensional extreme ground effect:
For a wing of small aspect ratio A -» 0,
Consideration of the expressions (6.114)—(6.117) shows that the aerodynamic coefficients Cy, mz, CXi/h, and Cs/h depend on the aspect ratio A and the parameter
![]() /cl
/cl
^ = T V 2h’
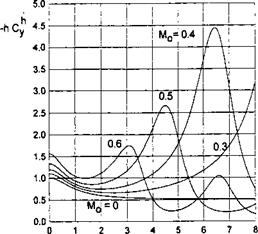
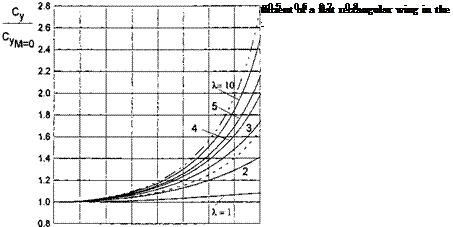
whereas the quantities Cyjк^тг/K^Cx. Jh^ and Cs/hn? depend only on the aspect ratio of the wing. Thus, for a wing of given aspect ratio it is sufficient, once and for all, to calculate the quantities Су/к^ тг/к, СХі/Нк? and Cs/hK?. Based on the data calculated in this way, it is easy to determine the aerodynamic characteristics, corresponding to different magnitudes of the jet momentum coefficient Cj and the relative ground clearance h. The parameter can be viewed as a similarity parameter that characterizes the aerodynamics of the wing with a jet flap in the extreme ground effect. Figure 6.11 illustrates the influence of the aspect ratio of a jet-flapped rectangular wing in the extreme ground effect upon the lift coefficient, related to the similarity parameter ftj.[30] The calculation was performed by using formula (6.114) with ten terms retained in the series, which converges very quickly. In the same figure there are plotted corresponding results for a wing of semielliptic planform; see Kida and Miyai [50].
|
C/x(z)=2Cjcos2y, |
We let the jet momentum coefficient distribution vary as
which is identical to the variation of the velocity of blowing along the span in proportion to cos(7tz/X). Then, the following formulas hold for the lift and the moment coefficients:
![Подпись: 0 1 2 3 4 5 x 6 Fig. 6.11. The influence of the aspect ratio on the lift coefficient of a jet-flapped flat wing of rectangular and semielliptic planform (solid line: rectangular planform, see formula (6.114); dashed line: semielliptic planform [50]).](/img/3131/image745.gif) |
4A [СЇ 7Г 4/2A,
= —rT ~r tanh — = —tanh л 7Г2 V h А 7Г2 Л
4A2T [C . 7Г 7Г
mz = —— —— tanh — tanh —.
7Г3 V h A 2A
Comparison of the lifting properties of a rectangular wing with a uniform jet momentum distribution and the jet momentum distribution, given by formula (6.125), shows that for the same angle of blowing, ground clearance, and the total jet momentum coefficients Cj, nonuniform blowing results in somewhat larger magnitudes of the lift coefficient than that of uniform blowing.
In section 9 a law of blowing is discussed, which leads to a minimum induced drag for a given lift coefficient and also the influence of optimization upon the lift-to-drag ratio of the wing with a jet flap in the ground effect.
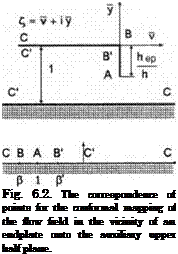
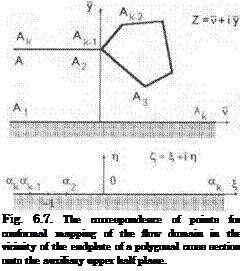
When the jet-flapped wing has endplates, the calculation of the lift coefficient and other aerodynamic coefficients can be performed taking into account the results presented in paragraph 6.1. Application of the approach set forth in paragraph 6.1 leads to the following formula for the relative lift coefficient of a jet-flapped wing with endplates:
Ky = ^ = 1 + hG( 7еР)4(А) + 0(Л2),
where the function G( jep) accounts for the configuration of the endplate and the function ylj, depending upon the aspect ratio, was found in the form
^ oo oo
Л (Л) = E C” tanh(?n ^ tanh qn/ql,
n=0 n—0
where
00 / і i
с« = Ё«2 + Л292/4’ 9п = д(2п + 1), ki = —(2/ + 1).
Leaving one term (l = n = 0) in this series, we can obtain the following approximate formula for ylj(A):
_ 16tanh(7rA/4)
7tA(4 + A2) tanh(7r/A) ’
It is remarkable that the magnitude of ylj from these formulas does not depend on the jet momentum.
Now some results will be discussed of the nonlinear theory of a jet – flapped wing of a finite aspect ratio in the extreme ground effect. For
a wing of rectangular planform, the aerodynamic coefficients can be derived in analytical form. Taking into account the trailing edge condition obtained earlier,
the nonlinear problem is formally described by the same set of equations except for the fact that the pressure distribution should be calculated by using the following nonlinear differential operator:
![]()
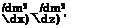
![]() (6.127)
(6.127)
Integrating the pressure difference (p) = p~ — on the wing surface taking into account the expression (6.127) for (f, we can derive the following expressions for the lift coefficient of a rectangular wing with a jet flap in the case of moderately large flow perturbations:
![]()
![]()
![]()
a
where
2 [X/2
 an=— (z) cos qnz dz, Kj(z)=r(z)
an=— (z) cos qnz dz, Kj(z)=r(z)
ЛЯп J — Л/2
|
a* tanhqnAg, |
The moment coefficient calculated around the trailing edge has been found in the form
For constant Kj = r JCfx/2h — т ^C-J2h, the following expressions were obtained for the coefficients of the lift, moment, and induced drag:
|
Cy ~ Kj (X 2. |
^ 16 ^ tanhgn / A2 2-, qs > 71=0 |
(6.130) |
|
16fti ^ tanhnn / mz= А» £ ,4 ( 71=0 |
tanh — j/Cj tanhgn^, |
(6.131) |
|
Cx. — hn2{ 1 — /^j |
^ 8 tanh2 qn )x2h й ‘ |
(6.132) |
As earlier, retaining just one term in the series (6.130)—(6.132), we obtain the following simple approximate formulas:
|
у 7Г3 A |
(6.133) |
|
16ftjA2 . 7Г / 7Г 1 _ 7T —– — tanh — (tanh ———- – K tanh — , 7Г4 A 2A 4 J А/ |
(6.134) |
|
„ _ 8Л«?(1 – Kj) ^_u2 7Г Cx. — о tanh. 7TJ A |
(6.135) |
For small magnitudes of Kj these formulas yield the corresponding formulas of linear theory. Of practical interest is an estimate of the maximum magnitudes of the lift coefficient of the a jet-flapped wing in the extreme ground effect. This maximum is achieved when the jet touches the ground, i. e., in the case
![]()
|
= — Y A2 ^ |
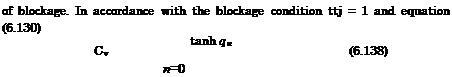 |
The magnitudes of the lift coefficient for other “nonblocking” magnitudes of parameter can be determined by taking into account (6.130) and (6.138) in the form
Су = Кj^l 2^^г/тах – (6.139)
It is interesting to compare the magnitudes of СУтлх, predicted by the nonlinear (6.138) and linear (6.114) theories. Due to the fact that the condition of blockage is identical for both the linear and nonlinear theories it follows immediately from (6.114) that for /cj = 1,
![]() cin = 16 tanh qn
cin = 16 tanh qn
2/max 2 / J n3
n=0 4n
Comparing expressions (6.130) and (6.138), we see that the linear theory predicts magnitudes of the maximum lift coefficient which are twice as large as those predicted by the nonlinear theory. It can be readily shown that the nonlinear description of the blockage phenomenon is closer to reality than the linear one. For instance, in the case of the wing of infinite aspect ratio, it follows from equations (6.138) and (6.140) that
£ГПОПІІП ^ £flin ___ 2
У max 5 У max "
At the same time, it is clear from the physical viewpoint that for zero or vanishing incidence the blockage of flow near the trailing edge of a wing of infinite aspect ratio moving near a wall, results in complete stagnation of the flow under the wing. In very close proximity to the ground, this situation corresponds to magnitudes of the lift coefficient close to unity.
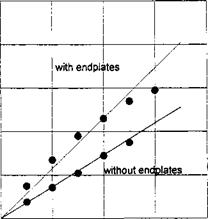
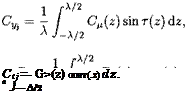 |
To conclude the consideration of the jet-flapped wing in the extreme ground effect, a comparison is presented in Fig. 6.12 of the results of the asymptotic theory with the experimental data of V. P. Shadrin, obtained in a wind tunnel for a rectangular wing with endplates. Note that, when conducting calculations by using the asymptotic theory, account was taken of the jet reaction force and the presence of the endplates. For large magnitudes of the blowing angle, the reactive components of the jet in the vertical and horizontal directions have to be predicted by the formulas
 |
It is worthwhile to mention that in the experiments conducted by Shadrin a model of a rectangular wing of aspect ratio Л = 1 with a “Gottingen” type foil section with an almost flat lower surface was tested. The relative thickness of the foil was equal to 11%, and the width of the jet injection slot with respect to the chord was 0.0053. Specially designed changeable trailing edge elements provided variation of the angle of blowing r, measured with respect to the flat lower surface of the wing. The injection of air was provided by special fans built into the model.











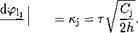 (6.86)
(6.86) – {Б2 – A2 + (0 + ^) (r^ + in
– {Б2 – A2 + (0 + ^) (r^ + in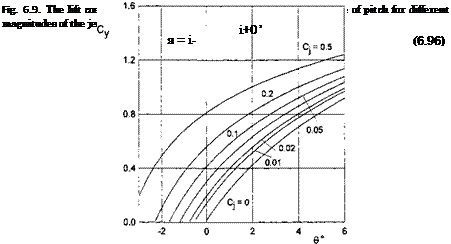
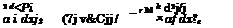 (6.51)
(6.51)

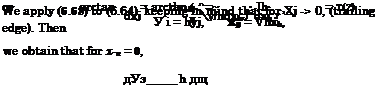
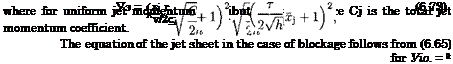


 0.0
0.0
 = 4 E”0(-l)ntanh2(gnA2/4)/g3
= 4 E”0(-l)ntanh2(gnA2/4)/g3
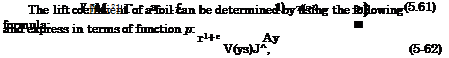
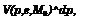
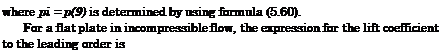

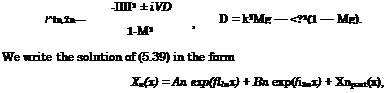
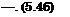
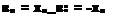 "part^n – «part exp(p2n)(Atln “ І&) ~ ЄХ-Р(Ціп)(М2п – Ік) The lift coefficient is obtained by integrating the loading
"part^n – «part exp(p2n)(Atln “ І&) ~ ЄХ-Р(Ціп)(М2п – Ік) The lift coefficient is obtained by integrating the loading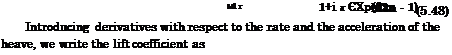

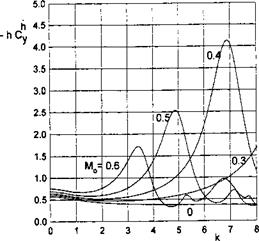

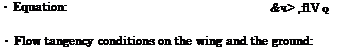

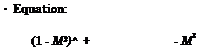
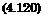 Unsteady Height Perturbation. In the case of height perturbation, h(x, t) = h(t). The perturbation potential can be represented as
Unsteady Height Perturbation. In the case of height perturbation, h(x, t) = h(t). The perturbation potential can be represented as
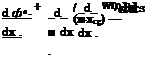
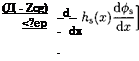
 1 – z – ^
1 – z – ^