Methods of Solution
Here we shall make a short review of some of the methods that have been proposed and used for solving the transonic nonlinear small-disturbance equations. The only case, so far, that has been found amenable to a mathematically exact treatment is the two-dimensional, for which it is possible to transform the nonlinear problem to a linear one by going to the hodograph plane. Let
0
n>
where Kx is given by (12-47). The quantities її and w represent (to first order), with appropriate constants, the components of the difference between the local velocity and the speed of sound. Thus, on the sonic line
її = 0, (12-55)
with w taking on any value, and
и = К i, w = 0
at infinity.
We may then write (12-12) with the aid of the condition of irrotation – ality as follows:
— йїїх + Wf = 0, (12-57)
щ = wx. (12-58)
We shall now transform this system so that и and w appear as the dependent variables. For this purpose we introduce a function ф(й, w) such that
x = fc, (12-59)
Ґ = Фіг – (12-60)
|
It will be shown subsequently that the irrotationality condition (12-58) is thereby automatically satisfied. For from (12-59) and (12-60) it follows that
_ Фиу) ~ D ’ (12-65) |
where
D — фиифигш (фиш)
is the functional determinant (Jacobian).
Similarly, it is found by use of (12-64) that
which confirms (12-58).
Proceeding in this manner we find that
^x — fiww/D
and
Щ = Фш/D-
Hence (12-57) transforms to
— Www + Фш = 0,
which is known as Tricomi’s equation after Tricomi (1923), who first investigated its properties. It is seen that the linear equation (12-69) preserves the mixed subsonic-supersonic character of the original equation because it is hyperbolic for її > 0 and elliptic for м < 0. However, the linearization of the equation has not been bought without considerable sacrifice to the simplicity in the application of the boundary conditions. In fact, solutions have so far been obtained only for some very simple shapes.
To illustrate the difficulties involved, the boundary conditions for a simple wedge are formulated in Fig. 12-7. The case of a subsonic free stream for which Кi < 0 is illustrated. In view of (12-54) the point й = Ki, = 0 represents infinity in the physical flow field so that, following
Fig. 12-7. The transonic flow around a nonlifting single wedge.
the definitions (12-59) and (12-60), the derivatives of ф must be infinite at this point, i. e., the solution must have a singularity at (Кb 0). The form of this may be determined from the linearized subsonic solution, except for M = 1 which requires special treatment.
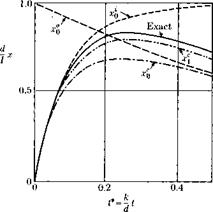
The transonic wedge solution has been worked out for M less than unity by Cole (1951) and by Yoshihara (1956), for M = 1 by Guderley and Yoshihara (1950), and for M > 1 by Yincenti and Wagoner (1952). The results for the drag coefficient are plotted in Fig. 12-8 together with experimental data obtained by Bryson (1952) and Liepmann and Bryson (1950). As seen, the agreement is excellent.
|
Fig. 12-8. Theoretical and experimental results for the drag of single-wedge airfoils. (From Spreiter and Alksne, 1958. Courtesy of the National Aeronautics and Space Administration.) |
The hodograph method is not very useful for axisymmetric flow, since the factor 1/p in the second term of (12-26) makes the equation still nonlinear after transformation to the hodograph plane. Because of such limitations, a considerable effort has been expended in finding methods that work directly in the physical plane. The solutions developed so far are all based on one or more approximations. In the method for twodimensional flow proposed by Oswatitsch (1950) and developed in detail by Gullstrand (1951), the differential equation is rewritten as an integral equation by the aid of Green’s theorem, and the nonlinear term is approximated under the implicit assumption that the value of an integral is less sensitive to errors in the approximations than is a derivative. Further improvements in this method have been introduced by Spreiter and Alksne (1955).
An approximation of a radically different kind was suggested by Os- watitsch and Keune (1955a) for treating the flow on the forward portion of a body of revolution at M = 1. In the differential equation (12-31) for M = 1,
— (7 + l)<Px<Pxx + – Vr + <Prr = 0, (12-70)
the nonlinear term was approximated by
(T – j – 1)iPx(Pxx = ^p*Pxj (12“71)
where the constant Xp is to be suitably chosen. The justification of this approximation is that on the forward portion of the body the flow is found to be everywhere accelerating at a fairly constant rate. Also, the resulting differential equation is parabolic, which intuitively is satisfying as an intermediate type between the elliptic and hyperbolic ones. The constant Xp was chosen arbitrarily (but in a way consistent with the similarity law) so as to give good agreement with the measured pressure distribution in one case, and it was proposed to use this as a universal value in other cases.
|
Fig. 12-9. Pressure distribution on a cone cylinder at iff = 1. (From Spreiter and Alksne, 1959. Courtesy of National Aeronautics and Space Administration.) |
Maeder and Thommen (1956) also used the approximation (12-71) for flows with M slightly different from unity and suggested a new, but still arbitrary, rule for determining Xp.
An interesting extension of Oswatitsch’s method, which removes the arbitrariness in selecting Xp, has been presented by Spreiter and Alksne (1959). In this the parabolic equation resulting from the approximation (12-71) is first solved assuming Xp constant, and the value of и = <ря is calculated on the body. Now (7 + 1 )ux is restored in place of Xp and a nonlinear differential equation of first order is obtained for u, which may be solved numerically. As an example, the pressure distribution on a slender cone-cylinder calculated this way is shown in Fig. 12-9 together with values obtained from the theory by Oswatitsch and Keune (1955) and measured values. As seen, the agreement with the improved theory is excellent and considerably better than with the original one.
Spreiter and Alksne (1958) also employed this technique with considerable success for two-dimensional flow, and for flows that have a Mach number slightly different from unity. In the latter case they replaced the nonlinear term
[1-М2 – M2(7 + l)Vx]Vtx (12-72)
by
X<p„, (12-73)
and proceeded similarly to solve the resulting linear equation with X constant. Thereupon (12-72) was resubstituted into the answer, producing a nonlinear first-order differential equation for и = <px as before. They were able to show that in the two-dimensional supersonic case, this gave an answer that was identical to that given by simple-wave theory.












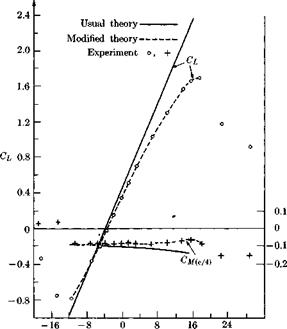
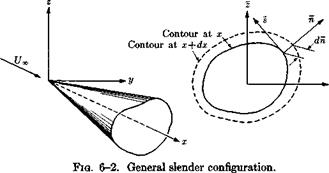

 a slender wing. T 1
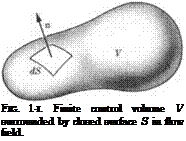
a slender wing. T 1 We turn to (1-15) and choose for S the cylindrical surface lying in a wall of the tube. Obviously, no vortex lines cross S, so that
We turn to (1-15) and choose for S the cylindrical surface lying in a wall of the tube. Obviously, no vortex lines cross S, so that ~dF
~dF