Linear Source/Quadratic Doublet Method
For this example, too, the approach of Section 11.3 is used and a combination of linearly varying strength sources and vortices will be distributed on the solid
|
FIGURE 11.34 Doublet distribution near the trailing edge of an airfoil. |
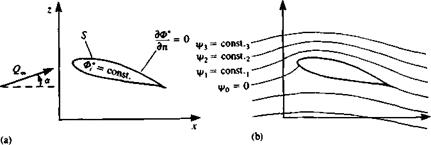
boundaries 5 (Fig. 11.34) and the vortex distribution is replaced by a quadratic doublet distribution. Following Section 11.3.1 the velocity potential within the volume enclosed by S is selected as Ф* = Фх and the boundary condition at each collocation point is reduced to the form given by Eq. (11.62):
S Bt°i + 2 с№ = 0 (11.62)
i=i j=i
where Ni is the number of singularity strength parameters. In this section a solution based on this equation using linearly varying source and quadratic doublet distributions will be established. The wake, however, will be modeled by a constant-strength doublet as shown in Fig. 11.34. Now, to develop the method of solution, let us follow the basic six step procedure.
Selection of singularity element. The potential at an arbitrary point P due to a linearly varying strength source element with the edge values of or oj+l was derived in the previous section and is given by Eq. (11.110):
Ф-? = PHILS (<jj, aj+ux, z, Xj, Zj, xj+l, zj+l) (11.110)
Similarly, the potential at point P due to a quadratic doublet distribution element where the doublet strength (in panel local coordinates) varies as
fl(x) = Ho + jUi-t + ц2х2
is obtained by combining Eqs. (10.28), (10.59), and (10.80):
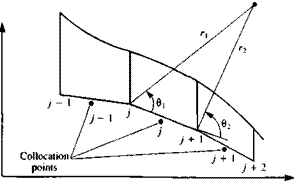
+ ^ (x2 – z2)(6i — в2) — xz In —f + z(xx – x2) panel coordinates (11.127) 2jtL r J
 |
|
where the variables r,, r2, ви and в2 are shown in Fig. 11.35.
When the point P is on the element (z = 0±, xl <x <x2) then this reduces to a combination of Eqs. (10.31), (10.64), and (10.84):
Ф(дг, 0±) = т(^ + ^ j panel coordinates (11.128)
Using the transformation of Eq. (11.23a) (from global to panel coordinates) and the above equations for the velocity potential an influence subroutine for the quadratic doublet element can be formulated such that
Ф
Ф" I
фй І = PHIQD [О*, /г,, fi2)j, x, z, xj, zjt xj+1, zj+i] (11.129)
ФC) D
This subroutine computes the potential at a point P due to the jth panel and the superscripts ( )“, ( )b and ( )c represent the panel influence contributions due to the terms in Eq. (11.127) multiplied by ц0, цх, and ц2, respectively. The increment in the potential at point P is therefore the sum of these three terms:
ф = фа + ф’’ + фс (11.130)
It is assumed that these three components of the velocity potential are automatically computed by this subroutine.
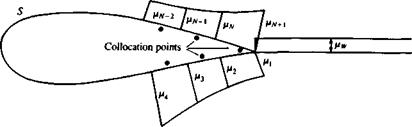
Discretization of geometry. The N + 1 panel corner points and N collocation points are generated in a manner similar to the previous examples (see Fig.
11.18) . In this case of the internal Dirichlet boundary condition the collocation points must be placed inside the body. This small inward displacement of the collocation point can be skipped if the panel self induced influence is specified in a separate formula.
Influence coefficients. The increment in the velocity potential at collocation point і due to a quadratic doublet element is computed by using Eq. (11.129) (note that a unit strength was assigned to all three doublet distribution coefficients Mo> Mi and ц2)-
For example, calculating the velocity potential increment by this formula for the first collocation point due to the first panel yields
(ФіМо + ф? і“і + фіМз)і = ЯпМої + Ь uMii + СцМіг
Here the first subscript of the doublets is used as the doublet parameter counter (0, 1, and 2) while the second subscript is the influencing panel counter. Similarly, for the coefficients a, b, and c the first counter is the collocation counter and the second is the influencing panel counter. The potential at this collocation point due to all the doublet panels is
фт = (fluMoi + bnMii + СцМ 21) + (аігМо2 + 612M12 + сі2М2г)
+ • • • + (ДшМолі + blN(iN + cwp2iv) + wPw (11.131)
where nw is the constant-strength wake doublet element (as in Section 11.3.1) and Axw is the wake influence coefficient which can be calculated by using Eq.
(11.66) . The strength of this wake doublet element (modeled by a constant strength doublet panel as shown in Fig. 11.34) is set by applying the Kutta condition at the trailing edge and is give by Eq. (11.118):
Mw = Mu — Ml (11.132)
where Mu and Ml are the upper and lower panel doublet strengths at the trailing edge, respectively.
Equations (11.131) for the potential can be formulated for each collocation point, resulting in N equations (for N panels) with 3N unknown (Mo, Мі» М2)/ and one more unknown, which is the wake doublet strength fiw. Additional equations can be obtained by requiring that the doublet distribution and its gradient will be continuous between neighboring elements. Applying this to the point between the yth and the (/ + l)th panel for the doublet strength results in
Mo/ + Ml/ Асу + М2/(ДС/)2 = Mo. z+1 (11-133fl)
and for the doublet gradient in
Мі/ + 2Мг/ ДCj = Mi,/+i (И-133*)
where A Cj is the panel length. Equations (11.133a and b) can be applied to all panel corner points, excluding the trailing edge, and thereby result in IN -2 equations. The last three equations are found as follows.
1. Equation (11.1336) can be applied at the trailing edge, so that the upper and lower doublet gradients will be equivalent:
Miai T 2мглг Дслі— M11 (11.134)
2. The Kutta condition is specified at the trailing edge by using Eq. (11.132).
Mw = MoN + Ml N Д CN + М2Лі(ДСЛі)2 — Мої (11.135)
3. The last “missing” equation can be obtained by specifying the Ф* = Ф* Dirichlet boundary condition (Eq. (11.62)) on an additional point inside the body. This equation will have the form of the regular N boundary conditions (e. g., as in Eq. (11.131)) and for best results it needs to be
specified near the trailing edge (e. g., on the camberline toward the trailing edge, inside a thick airfoil, or between the upper and lower trailing edge collocation points).
Establish RHS vector. The boundary condition given by Eq. (11.62) is specified at the N + 1 collocation points and the strength of the sources will be specified by using Eq. (11.61) (note that in this case the panel edge source values Oj are evaluated at the panel edges).
a; = n,-Q» (11.61)
Since the source contribution to the velocity potential is now known, the potential due to all the N panels (with N + 1 panel edge source values) can be computed by using Eq. (11.120) such that
N
RHS, = – ‘Z PHILS (Oj, oj+x, xh zh xj, Zj, xj+1, z,+1) (11.120)
y=i
The right-hand side vector RHS, is now evaluated at the N collocation points plus at the (N + l)th point (which was selected inside the body and near the trailing edge).
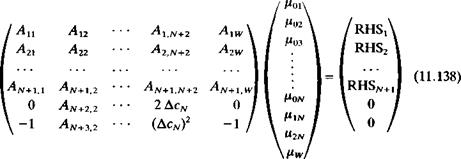
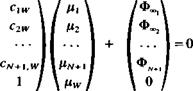
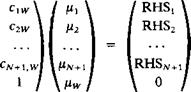
Solve Equations. At this point it is possible to establish N + 1 equations based on the boundary condition (Eq, (11.62)) plus two equations based on the trailing edge conditions (Eqs. (11.134) and (11.135)) and they will have the following form:

 Я 11^11C11 fl21^21c21
Я 11^11C11 fl21^21c21
аЛ! +1,1 ^ ЛМ-1,1+1,1
![]() -1, 0
-1, 0
о, 0
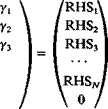
RHS,
 |
rhs2
In this equation the matrix will have 3N + 1 columns (same as the ц vector) and N + 3 rows (same as the RHS vector). The additional 2(N – 1) equations
can be obtained by using Eqs. (11.133-11.135). However, from the computational point of view it is desirable to reduce the influence matrix size, which can be done by substituting the above equations backward while calculating the influence matrix.
It is possible to rearrange Eqs. (11.133a and b) to create a regression formula such that
2
f*u = (/*o,/+i – Hot) – Hi. j+i (11.137a)
^ = 2^с-^1,]+1~iU, y) (11.137b)
 |
Using these regression equations, all july and y.2j can be eliminated (by performing column operations on the matrix), excluding the last two (nXN and H2n)- These algebraic operations can be performed automatically when assembling the matrix coefficient and will reduce Eq. (11.136) to the form
where now we have N + 3 equations with N + 3 unknowns /Xoi, jUo2,. . . , Hon> Pin, Pin, Hw and AXj are the new coefficients obtained after the resubstitution process.
Solve equations. Solution of the full-matrix equation (Eq. (11.138)) with N + 3 unknown values цк can be obtained by standard matrix solvers. Then the local panel doublet distribution can be obtained by using the same regression formulation that was used to reduce the number of columns in the influence coefficient matrix.
Calculation of pressures and loads. Once the values of the doublet parameters {fxoi, |Uo2. . • • , Ho> Hin> 1*2n) are known, the panel doublet distribution can be calculated. Then the perturbation velocity at each collocation point can be calculated by using the tangential derivative of the doublet at the panel center and the total tangential velocity becomes
![]() Qi, = Qt„ + (му + 2^2i~y)
Qi, = Qt„ + (му + 2^2i~y)
and the pressure coefficient can be calculated by using Eq. (11.18). The lift and pitching moment of the panel can be obtained by using the method described by Eqs. (11.78-11.80).
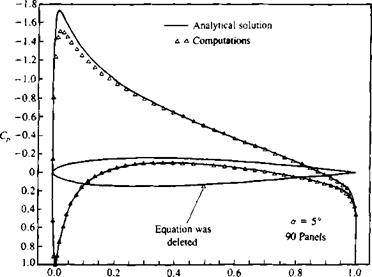
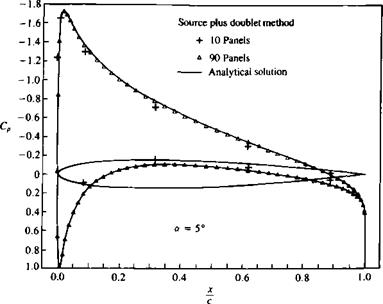
A computer program based on the quadratic doublet is presented in Appendix D and the formulation of the doublet only method is very similar to this one. The pressure coefficients computed with this method for the airfoil of Section 6.6 at an angle of attack of 5° are very similar to the data presented in Fig. 11.31.












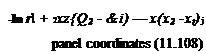
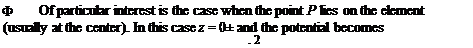
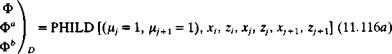 (
(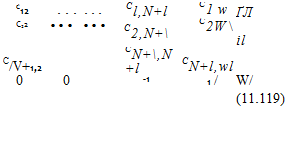


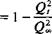 (11.18)
(11.18)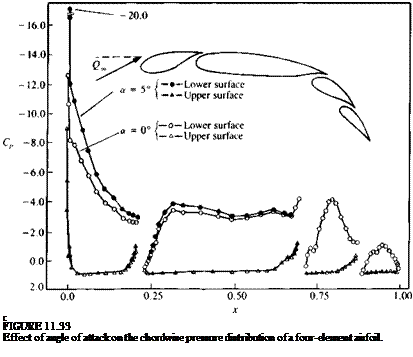
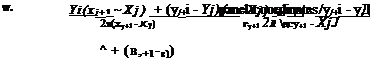
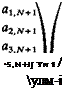
 a 12
a 12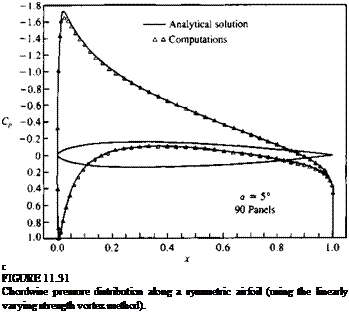
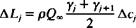 (11.107)
(11.107)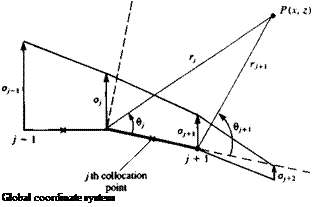
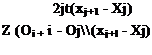 4+1
4+1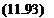 ua, wa I = SOR2DL(a/( oj+u x, z, Xj, Zj, x.+1, zj+1)
ua, wa I = SOR2DL(a/( oj+u x, z, Xj, Zj, x.+1, zj+1)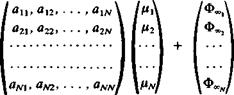 (11.83)
(11.83)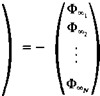

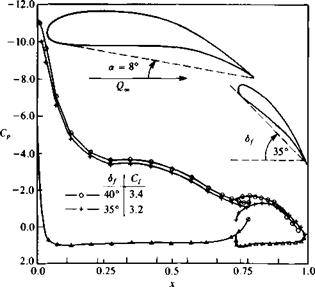
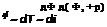
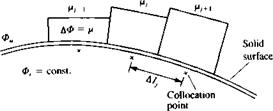 FIGURE 11.26
FIGURE 11.26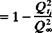 (11.77)
(11.77)
 panel coordinates (11.44)
panel coordinates (11.44)
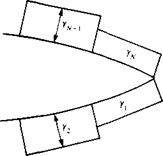 Constant-strength vorticity panels near the trailing edge of an airfoil.
Constant-strength vorticity panels near the trailing edge of an airfoil.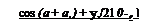
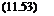 Cp = –
Cp = –