Constant-Strength Doublet Method
The simplest two-dimensional panel code that can calculate the flow over thick lifting airfoils is based on the constant-strength doublet. The surface pressure distribution computed by this method is satisfactory on the surface, but since this element is equivalent to two concentrated vortices at the edges of the element, near-field off-surface velocity computations will have the same fluctuations as shown in Fig. 11.11 (but the velocity calculated at the collocation point and the resulting pressure distribution are correct).
Selection of singularity element. Consider the constant-strength doublet element of Section 10.2.3 pointing in the positive z direction, where the panel is based on a flat element. To establish a normal-velocity boundary condition based method, the induced velocity formulas of Eqs. (10.29) and (10.30) are used (which are equivalent to two point vortices with a strength ц at the panel edges)
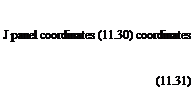 = Г_________ £______________ z_
= Г_________ £______________ z_
Up 2n L(x – Xj)2 + z2 (x-x2)2 + z2
-/*[ X~XA X~X2 1 .
2л l(x-xt)2 + z2 (x-x2)2 + z2 pane
Here, again, the velocity components (и, w)p are in the direction of the panel local coordinates, which need to be transformed back to the x-z system by Eq.
(11.23) .
This procedure can be included in an induced-velocity subroutine DUB2DC (where C stands for constant) that will compute the velocity (и, w) at an arbitrary point {x, z) due to the jth element:
![]() (u, w) = DUB2DC x, z, xjt zjt xj+u zj+l)
(u, w) = DUB2DC x, z, xjt zjt xj+u zj+l)
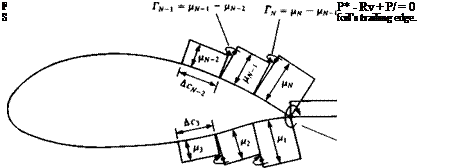
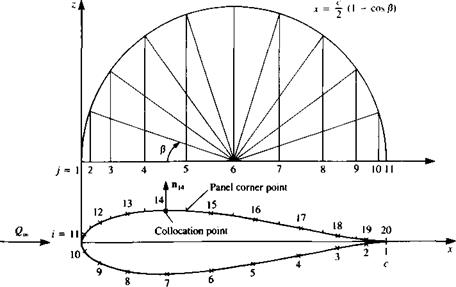
Discretization of geometry. The panel corner points and collocation points are generated exactly as in the previous section (see Fig. 11.18). However, in this lifting case, a wake panel shown in Fig. 11.20 has to be specified. This doublet element will have a strength juw and extends to x = In practice, the far portion (starting vortex) of the wake will have no influence and can be placed far downstream [e. g., at (°°, 0)].
 |
Influence coefficients. To obtain the normal component of the velocity at a collocation point (e. g., the first point) due to the y’th doublet element, Eq.
(11.32)
is used
The influence coefficients a, y are defined as the velocity components normal to the surface. Consequently, the contribution of a unit strength singularity element j, at collocation point 1, is
av = (и. w)y • “і
Similarly to the case of the constant-source method, the influence coefficients can be found by using Eq. (11.27):
![]() (11.27)
(11.27)
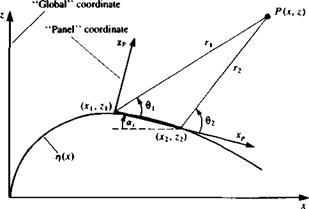
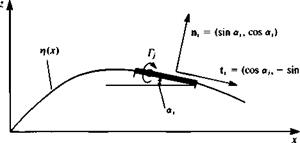
where a-, and at are the first and the )th panel angles, as defined in Fig. 11.17, and (uv, wiy)p are the velocity components of Eqs. (11.30) and (11.31) due to a unit-strength element as measured in the panel frame of reference.
To evaluate the influence of the element on itself, at the center of the panel, Eqs. (10.32) and (10.33) are recalled
![]() (11.34)
(11.34)
(11.35)
Consequently, when і = j the influence coefficient becomes
![]() 2
2
|
|
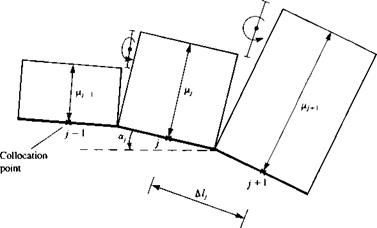
where ДCj is the ith panel chord.
Establish boundary condition (RHS). The free-stream normal velocity component RHS, is found as in the previous examples (e. g., by using Eq. (11.6)).
Solve equations. Specifying the boundary condition of Eq. (11.4) for each (i = 1 —» N) of the collocation points results in a set of algebraic equations with the unknown fij (j = l-*N). However, observing the equivalent vortex representation in Fig. 11.20 reveals that the strength of the vortex at the trailing edge is Г = Mi – Hn – Recalling the Kutta condition that the circulation at the trailing edge is zero requires the addition of a wake panel that will cancel this vortex:
(м і AOv) + №w — 0 (11.36)
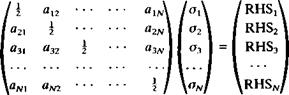
A combination of this equation with the N boundary conditions results in N + 1 linear equations:
|
a in «iw J «2IV a2W | A*2 «AW °NW j ~ 1 1 / /zw/ |
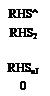
![]() «п
«п
«21
am
This system of equations is the numerical equivalent of the boundary condition (Eq. (11.4)) and is well defined and will have a stable solution.
Calculation of pressures and loads. Once the strength of the doublets /і/ is known, the perturbation tangential velocity component at each collocation point can be calculated by summing the induced velocities of all the panels, using Eq. (11.33). The tangential velocity at collocation point i is then
N+1
q,, = 2 (“. w)a • t, (11.37)
7 = 1
where (и, w)q is the result of Eq. (11.33) and t, is the local tangent vector defined by Eq. (11.3a) and the (N + l)th component is due to the wake. Note that to evaluate the tangential velocity component induced by a panel on itself Eq. (3.141) can be used:
1 du(l)
Я, = 2 ~дГ onPanel (11.38)
where l represents distance along a surface line. So when evaluating the tangential component of the perturbation velocity the result of Eq. (11.38) must be included (when і = j in Eq. (11.37)). The pressure coefficient can be computed by using Eq. (11.18):
![]() r = і + fr)/
r = і + fr)/
Qi
|
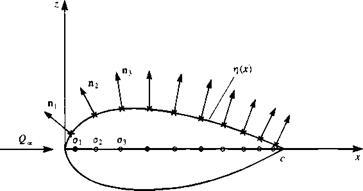
FIGURE 11.21 Typical segment of constant-strength doublet panels on the airfoil’s surface. |
where
(<2J, = tyQ~ (11.39a)
Note that the local lift can be calculated, too, by using the Kutta Joukowski formula for a point vortex:
ALj = pQS, = —P0oo(/i,+i “ Py) (11.40)
where the minus sign is used for doublet panels pointing outside the airfoil. This formulation should be equivalent to the result that we get by assuming constant pressure on the panel,
ACtj = —CP/ Alj cos ос, (11.41)
where A lj and ay are shown in Fig. 11.21. The total lift and moment are obtained by integrating the contribution of each element:
L = 2>Ly (11.42)
i=і N
M„= 2 ALj(xj cos a) (11.43)
y=і
and the nondimensional coefficients can be calculated by using Eqs. (11.12) and (11.13).
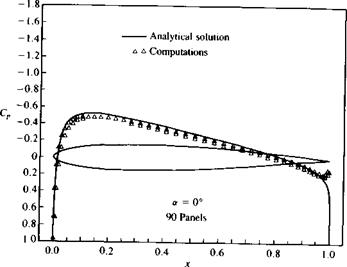
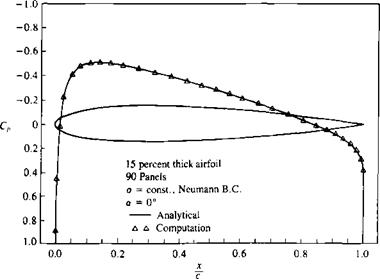
Example 1 Lifting thick airfoil. The above method was used for computing the pressure distribution over the airfoil of Section 6.6, as shown in Fig. 11.22. The data agrees satisfactorily with the analytic solution for both the zero (Fig. 11.22a) and five-degree angle-of-attack conditions (Fig. 11.226). A slight disagreement is
|
|
|
c |
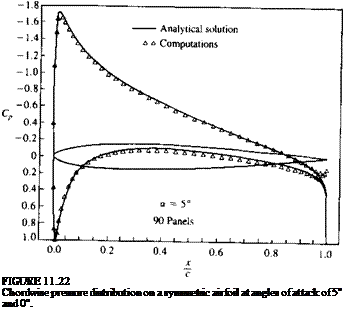 |
visible near the maximum suction area and near the rear stagnation point. These results can be improved by moving the grid and the collocation points near these areas, but such an optimization procedure is not carried out here. The computer program used for this example is included in Appendix D (Program No. 3).











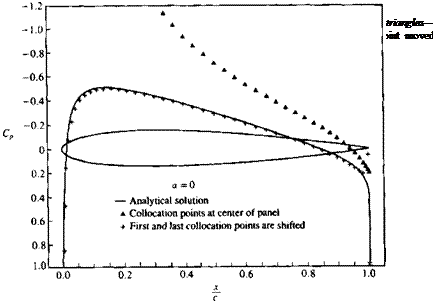
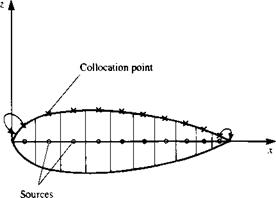 Relocation of the first and last collocation point to improve the numerical solution with the discrete source method.
Relocation of the first and last collocation point to improve the numerical solution with the discrete source method.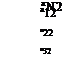
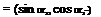
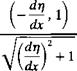 (11.3)
(11.3)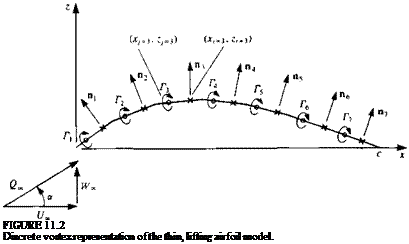
 ~4 Ac K
~4 Ac K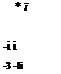
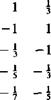
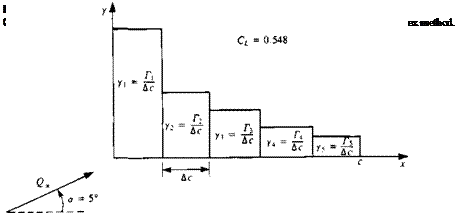
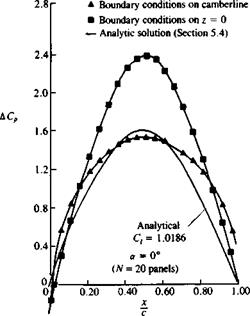
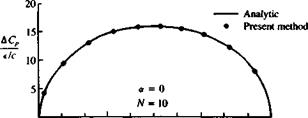

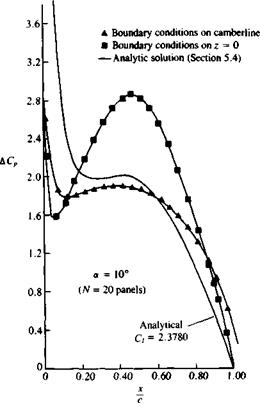
 FIGURE 11.10
FIGURE 11.10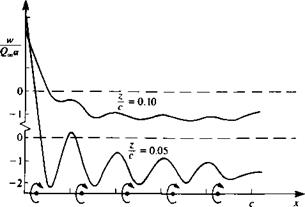
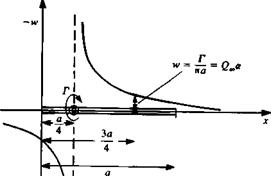
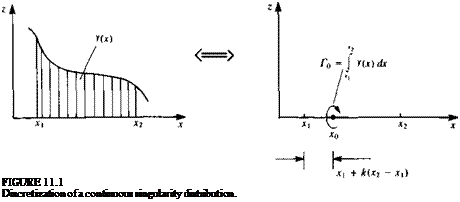
 . / ЭФ ЗФ ЭФ
. / ЭФ ЗФ ЭФ
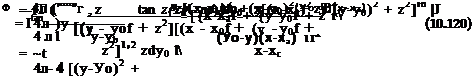
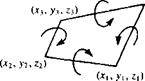
 FIGURE 10.24
FIGURE 10.24 X у z *1 У z2 x2 У2 Z2 *3 Уз z3 X4 y4 z4
X у z *1 У z2 x2 У2 Z2 *3 Уз z3 X4 y4 z4 FIGURE 10.25
FIGURE 10.25