Category AIRCRAF DESIGN

A civil aircraft fuselage is designed to carry revenue-generating payloads, primar­ily passengers but the cargo version can also carry containers or suitably packaged cargo. It is symmetrical to a vertical plane and maintains a constant cross-section with front and aft-end closures in a streamlined shape. The aft fuselage is subjected to adverse pressure gradients and therefore is prone to separation. This requires a shallow closure of the aft end so that the low-energy boundary layer adheres to the fuselage, minimizing pressure drag (see Section 3.3). The fuselage also can pro­duce a small amount of lift, but this is typically neglected in the conceptual stages of a configuration study. The following definitions are associated with the fuselage geometry (Figure 3.49).

1.23.1 Fuselage Axis/Zero-Reference Plane

Fuselage axis is a line parallel to the centerline of the constant cross-section part of the fuselage barrel. It typically passes through the farthest point of the nose cone,

facilitating the start of reference planes normal to it. The fuselage axis may or may not be parallel to the ground. The principal inertia axis of the aircraft can be close to the fuselage axis. In general, the zero-reference plane is at the nose cone, but design­ers can choose any station for their convenience, within or outside of the fuselage. This book considers the fuselage zero-reference plane to be at the nose cone, as shown in Figure 3.49.

Canard is French for “goose,” which in flight stretches out its long neck with its bulbous head in front. When a horizontal surface is placed in front of the aircraft, it presents a similar configuration; hence, this surface is sometimes called a canard.

The Wright Brothers’ Flyer had a control surface at the front (with a destabi­lizing effect), which resulted in a sensitive control surface. Military aircraft use a canard to enhance pitch control. However, the use of a canard in civil aircraft appli­cations serves a different purpose (Figure 3.48).

In general, the inherent nose-down moment (unless a reflex trailing edge is employed) of a wing requires a downward force by the H-tail to maintain level flight. This is known as trimming force, which contributes to trim drag. For an extreme CG shift (which can happen as fuel is consumed), high trim drag can exist in a large por­tion of the cruise sector. The incorporation of a canard surface can reduce trim drag as well as the H-tail area, SH. However, it adds to the manufacturing cost and, until recently, the benefit from the canard application in large transport aircraft has not been marketable.

Many small civil aircraft have a canard design (e. g., Rutan designs). A successful Bizjet design is the Piaggio P180 Avanti shown in Figure 3.48. It has achieved a very high speed for its class of aircraft through careful design considerations embracing not only superior aerodynamics but also the use of composite materials to reduce weight.

Canard Volume Coefficient, CCt

This also is derived from the pitching-moment equation for steady-state (i. e., equi­librium) level flight. The canard reference area, SC, has the same logic for its defini­tion as that of the H-tail. Its tail arm is LCT. The canard reference area is given as:

Sct = (Cct)(Sw x MAC)/Lct, (3.48)

where CCT is the H-tail volume coefficient, 0.5 < CHT < 1.2; a good value is 0.6 to 0.9, depending on whether it is a conventional H-tail. The LCT is the H-tail arm = distance between the aircraft CG to the ac of MACCT. In general, SCT/SW & 0.2 to 0.3.

From the yawing-moment equation (see Chapter 12) for steady-state (i. e., equilib­rium) level flight, the V-tail volume coefficient is given as the V-tail plane reference area:

where CVT is the V-tail volume coefficient, 0.05< CVT <0.1; a good value is 0.07. LVT is the H-tail arm = distance between the aircraft CG to the ac of MACVT. In general, the area ratio SVT/SW ^ 0.15 to 0.25.

Chapter 6 describes how to estimate the empennage areas; a number of design iterations are necessary. Figures 12.15 and 12.16 give statistical values of tail volume coefficients.

Tail volume coefficients are used to determine the empennage reference areas, SH and SV. The definition of the tail volume coefficients is derived from the aircraft stability equations provided herein. The CG position (see Chapter 8) is shown in Figure 3.47. The distances from the CG to the aerodynamic center at the MAC of the V-tail and H-tail (i. e., MACvt and MACht) are designated Lht and Lvt, respectively, as shown in Figure 3.47. The ac is taken at the quarter-chord of the MAC.

H-Tail Volume Coefficient, Cht

From the pitching-moment equation (see Chapter 12) for steady-state (i. e., equilib­rium) level flight, the H-tail volume coefficient is given as the H-tail plane reference area:

Sht = (Cht)(Sw x MAC)/Lht, (3.46)

where Cht is the H-tail volume coefficient, 0.5< Cht <1.2; a good value is 0.8. Lht is the H-tail arm = distance between the aircraft CG to the ac of MACht. In general, the area ratio Sht/Sw & 0.25 to 0.35.

The H-tail consists of the stabilizer (fixed or moving) and the elevator (moving) for handling the pitch degree of freedom (Figure 3.46a). The H-tail can be positioned low through the fuselage, in the middle cutting through the V-tail, or at the top of the V-tail to form a T-tail (see Figure 3.33).

Military aircraft can have all moving H-tails with emergency splitting in case there is failure, and there are several choices for positioning it (see Chapter 4). Figure 3.46a shows the geometrical definition of conventional-type H-tail surfaces. Like the wing planform definition, the H-tail reference area, SH, is the planform area including the portion buried inside the fuselage or V-tail for a low – or mid-tail location, respectively. The T-tail position at the top has a fully exposed planform.

3.22.1 V-Tail

The V-tail consists of a fin (fixed) and a rudder (moving) to control the roll and yaw degrees of freedom (see Figure 3.46). The figure shows the geometrical defini­tion of a conventional-type V-tail surface reference area, SV. The projected trape – zoidal/rectangular area of the V-tail up to this line is considered the reference area, SV. Depending on the closure angle of the aft fuselage, the root end of the V-tail is fixed arbitrarily through a line drawn parallel to the fuselage centerline, passing through the point where the midchord of the V-tail intersects the line.

Typically, the empennage consists of horizontal and vertical tails for aircraft stability and control. Various types of empennage configurations are described in Chapter 4. The dominant type has a vertical tail (V-tail; U. K. terms are fin and rudder) in the plane of symmetry with a symmetrical aerofoil. A horizontal tail (H-tail; U. K. terms are stabilizer and elevator) is like a small wing at the tail (i. e., the aft end of the fuselage). The last two decades have seen the return of aerodynamic surfaces placed in front of the wing (see Figure 3.48); these are called canards and are discussed in subsequent chapters. This section addresses the definitions associated with the empennage and canard as well as the tail volume coefficients (see Chapter 12).

The V-tail of a single-engine, propeller-driven aircraft may have an offset of 1 to 2 deg to counter the effects of rotating propeller slipstream.

Sections 3.11 through 3.20 cover a wide range of wing design features. This section describes the considerations necessary to finalize the wing design. Selection of the aerofoil is the most important initial task. The wing aerofoil t/c ratio is established for the maximum cruise speed by the choice of aerofoil and sweep. It can vary along the span, with the root demanding the thickest section to withstand the bending moment. Once the aerofoil is selected, six parameters must be established for wing design: (1) wing planform area, (2) wing aspect ratio, (3) wing span, (4) wing sweep, (5) wing dihedral, and (6) wing twist.

1. Establish the wing reference area (see Chapter 11).

2. Establish the wing planform geometry (i. e., the maximum aspect ratio per­mitted by the structural technology). The statistics provided previously are a good guide. A new design should have higher aspect ratios compared to current designs.

Figure 3.46. Horizontal tail and vertical tail

3. Establish the wing sweep for the Mach number of operations.

4. Establish the wing span from the previous three steps. For commercial transport aircraft, the wing span is currently restricted to a maximum of 80 m.

5. Establish the wing dihedral and anhedral angles; it is generally within 1 to 5 deg for the dihedral.

6. Establish the wing twist; it is usually within 1 to 2 deg (generally downwash).

At the conceptual stage, the twist, dihedral, and anhedral are taken from experi­ence. Subsequently, CFD analyses can fine-tune all related parameters for the best compromise. Ultimately, wind-tunnel tests are required to substantiate the design.

Flaps and slats on a 2D aerofoil are described in Section 3.10. This section describes their installation (Figure 3.43a) on a 3D wing.

Flaps comprise about two thirds of an inboard wing at the trailing edge and are hinged on the rear spar (positioned at 60 to 66%; the remaining third by the aileron) of the wing chord, which acts as a support. Slats run nearly the full length of the LE. The deployment mechanism of these high-lift devices can be quite complex. The associated lift-characteristic variation with incidence is shown in Figure 3.43b. Slat deployment extends the wing maximum lift, whereas flap deployment offers incremental lift increase at the same incidence.

The aileron acts as the roll-control device and is installed at the extremities of the wing for about a third of the span at the trailing edge, extending beyond the flap. The aileron can be deflected on both sides of the wing to initiate roll on the desired side. In addition, ailerons can have trim surfaces to alleviate pilot loads. A variety of other devices are associated with the wing (e. g., spoiler, vortex generator, and wing fence).

Spoilers (or lift dumpers) (Figure 3.44) are flat plates that can be deployed nearly perpendicular to the airflow over the wing. They are positioned close to the CG (i. e., X-axis) at the MAC to minimize the pitching moment, and they also act as air brakes to decrease the aircraft speed. They can be deployed after touchdown at landing, when they would “spoil” the flow on the upper wing surface, which destroys the lift generated (the U. S. terminology is lift dumper). This increases the ground reaction for more effective use of wheel brakes.

Many types of wing tip devices reduce induced drag by reducing the intensity of the wing tip vortex. Figure 3.44 shows the prevalent type of winglets, which modify the tip vortex to reduce induced drag. At low speed, the extent of drag reduction is minimal and many aircraft do not have a winglet. At higher speeds, it is now recognized that there is some drag reduction no matter how small, and it has begun to appear in many aircraft – even as a styling trademark on some. The Blended

winglet and Whitcomb types are is seen in high-subsonic aircraft. The Hoerner type and sharp-raked winglet are used in lower-speed aircraft.

The Whitcomb-type wing tip and its variants without the lower extension are popular with high-subsonic turbofan aircraft. Extensive analyses and tests indicate that approximately 1% of induced-drag reduction may be possible with a carefully designed winglet. Until the 1970s and 1980s, the winglet was not prominent in air­craft. In this book, no credit is taken for the use of the winglet. Coursework can incorporate the winglet in project work.

Wing flow modifier devices (Figure 3.45) are intended to improve the flow qual­ity over the wing. In the figure, a fence is positioned at about half the distance of the wingspan. The devices are carefully aligned to prevent airflow that tends to move spanwise (i. e., outward) on swept wings.

Figure 3.45 also shows examples of vortex generators, which are stub wings care­fully placed in a row to generate vortex tubes that energize flow at the aft wing. This enables the flow to remain attached; however, additional drag increase due to vortex generators must be tolerated to gain this benefit.

Vortex generators and/or a fence also can be installed on a nacelle to prevent separation.

Stalling of conventional wings, such as those configured for high-subsonic civil air­craft, occurs around the angle of attack, a, anywhere from 14 to 18 deg. Difficult maneuvering demanded by military aircraft requires a much higher stall angle (i. e., 30 to 40 deg). This can be achieved by having a carefully placed additional low – aspect-ratio lifting surface – for example, having a LE strake (e. g., F16 and F18) or a canard (e. g., Eurofighter and Su37). BWB configurations also can benefit from this phenomenon.

At high angles of attack, the LE of these surfaces produces a strong vortex tube, as shown in Figure 3.42, which influences the flow phenomenon over the main wing. Vortex flow has low pressure at its core, where the velocity is high (refer to aerody­namic textbooks for more information).

The vortex flow sweeping past the main wing reenergizes the streamlines, delay­ing flow separation at a higher angle of attack. At airshows during the early 1990s, MIG-29s demonstrated flying at very high angles of attack (i. e., above 60 deg); their transient “cobra” movement had never before been seen by the public.

For an example, increase the linear dimensions of a solid cube from 1 to 2 units. From the following example, it can be seen that the increase in weight is faster than the increase in area (the subscript 1 represents the small cube and the subscript 2 represents the larger cube):

area2 = area1 x (length2/length^2, a 4-fold increases from 6 to 24 square units volume2 = volume1 x (length2/length1)3, an 8-fold increase from 1 to 8 cube units

Applying this concept to a wing, increasing its span (i. e., linear dimension, b – main­taining geometric similarity) would increase its volume faster than the increase in surface area, although not at the same rate as for a cube. Volume increase is asso­ciated with weight increase, which in turn would require stiffening of the struc­ture, thereby further increasing the weight in a cyclical manner. This is known as the square-cube law in aircraft design terminology. This logic was presented a half­century ago by those who could not envisage very large aircraft.

weight, W a span3 wing planform area, Sw a span2 (3.43)

Then,

wing-loading, W/Sw a b

This indicates that for the given material used, because of excessive weight growth, there should be a size limit beyond which aircraft design may not be feasible. If the fuselage is considered, then it would be even worse with the additional weight.

Yet, aircraft size keeps growing – the size of the Airbus A380 would have been inconceivable to earlier designers. In fact, a bigger aircraft provides better structural efficiency, as shown in Figure 4.6, for operating empty weight fraction (OEWF) reduction with maximum takeoff weight (MTOW) gain. Researchers have found that advancing technology with newer materials – with considerably better strength – to-weight ratio, weight reduction by the miniaturization of systems, better high-lift devices to accommodate higher wing-loadings, better fuel economy, and so forth – has defied the square-cube law. Strictly speaking, there is no apparent limit for fur­ther growth (up to a point) using the current technology.

The author believes that the square-cube law needs better analysis to define it as a law. Currently, it indicates a trend and is more applicable to weight growth with an increase in aspect ratio. What happens if the aspect ratio does not change? The following section provides an excellent example of how a low aspect ratio can compete with a high aspect-ratio design.

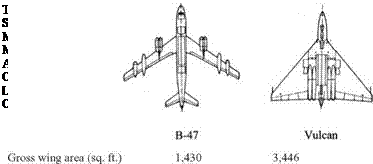
Figure 3.41. Torenbeek’s comparison between a B-47 and a Vulcan

3.20.2 Aircraft Wetted Area (AW) versus Wing Planform Area (Sw)

The previous section raised an interesting point on aircraft size, especially related to wing geometry. This section discusses another consideration on how the aircraft wing planform area and the entire aircraft wetted surface areas can be related. Again, the wing planform area, SW, serves as the reference area and does not account for other wing parameters (e. g., dihedral and twist).

The conflicting interests between aerodynamicists and stress engineers on the wing aspect ratio presents a challenge for aircraft designers engaged in conceptual design studies (this is an example of the need for concurrent engineering). Both seek to give the aircraft the highest possible lift-to-drag (L/D) ratio as a measure of efficient design. Using Equations 3.23 and 3.31, the following can be shown (i. e., incompressible flow):

drag, D = qSwCD = qSw(CDP + Cdi )

or

CD = (Cdp + CDi) (3.44)

Clearly, CDP a wetted area, AW and CDi is a (1/AR) = SW/b2 (from Equa­tion 3.43).

Define the wetted-area aspect ratio as follows:

ARwet = b2 / Aw = AR/( Aw / Sw) (3.45)

This is an informative parameter to show how close the configuration is to the wing – body configuration. Section 4.5 provides statistical data for various designs.

Torenbeek [5] made a fine comparison to reveal the relationship between the aircraft wetted area, AW, and the wing planform area, Sw. Later, Roskam [6] presented his findings to reinforce Torenbeek’s point, whose result is shown in Figure 3.41.

Toreenbeck compared an all-wing aircraft (i. e., the Avro Vulcan bomber) to a conventional design (i. e., Boeing B47B bomber) with a similar weight of approxi­mately 90,000 kg and a similar wing span of about 35 m. It was shown that these designs can have a similar L/D ratio despite the fact that the all-wing design has an aspect ratio less than one third of the former. This was possible because the all-wing aircraft precludes the need for a separate fuselage, which adds extra surface area and thereby generates more skin-friction drag. Lowering the skin-friction drag by having a reduced wetted area of the all-wing aircraft compensates for the increase in induced drag for having the lower aspect ratio.

All-wing aircraft provide the potential to counterbalance the low aspect ratio by having a lower wetted area. Again, the concept of BWB gains credence.

Table 3.1 provides statistical information to demonstrate that a BWB is a good design concept to satisfy both aerodynamicists and stress engineers with a good L/D ratio and a low-aspect-ratio wing, respectively. In the table, a new parameter – wet­ted aspect ratio, b2/AW = AR/(AW/SW) – is introduced.

The table provides the relationship among the aspect ration, wing area, and wet­ted area and how it affects the aircraft aerodynamic efficiency in terms of the ratio. Within the same class of wing planform shape, the trend shows that a higher aspect ratio provides a better L/D ratio. However, all-wing aircraft (e. g., BWB) provide an interesting perspective, as discussed in this section.