Transonic Effects – Area Rule
At high subsonic speeds, the local velocity along a curved surface (e. g., on an aerofoil surface) can exceed the speed of sound, whereas flow over the rest of the surface
|
Typical flat upper surface with aft camber for rear loading Figure 3.22. Transonic flow (supercritical Whitcomb aerofoil) |
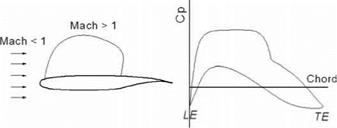
remains subsonic. In this case, the aerofoil is said to be in transonic flow. At higher angles of attack, transonic effects can appear at lower flight speeds. Aerofoil – thickness distribution along the chord length is the parameter that affects the induction of transonic flow. Transonic characteristics exhibit an increase in wave drag (i. e., the compressibility effect; refer to aerodynamic textbooks). These effects are undesirable but unavoidable; however, aircraft designers keep the transonic effect to a minimum. Special attention is necessary in generating the aerofoil section design, which shows a flatter upper surface. Figure 3.22 depicts a typical transonic aerofoil (i. e., the Whitcomb section) and its characteristics.
The Whitcomb section, which appeared later, advanced the flight speed by minimizing wave drag (i. e., the critical Mach-number effects); therefore, it is called the supercritical aerofoil section. The geometrical characteristics exhibit a round LE, followed by a flat upper surface and rear-loading with camber; the lower surface at the trailing edge shows the cusp. All modern high-subsonic aircraft have the supercritical aerofoil section characteristics. Manufacturers develop their own section or use any data available to them.
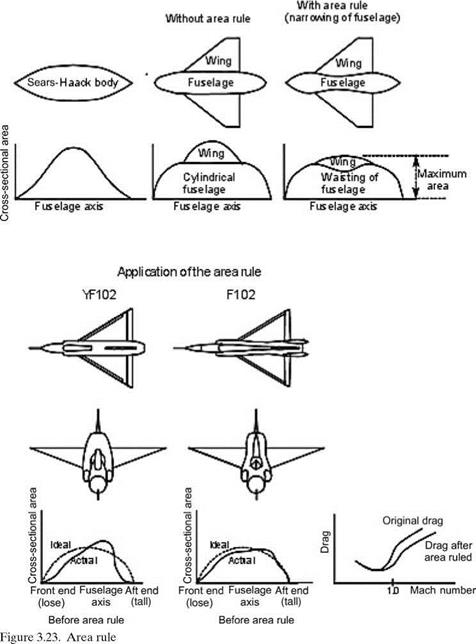
For an aircraft configuration, it has been shown that the cross-sectional area distribution along the body axis affects the wave drag associated with transonic flow. The bulk of this area distribution along the aircraft axis comes from the fuselage and the wing. The best cross-sectional area distribution that minimizes wave drag is a cigar-like smooth distribution (i. e., uniform contour curvature; lowest wave drag) known as the Sears-Haack ideal body (Figure 3.23). The fuselage shape approximates it; however, when the wing is attached, there is a sudden jump in volume distribution (Figure 3.23). In the late 1950s, Whitcomb demonstrated through experiments that “waisting” of the fuselage in a “coke-bottle” shape could accommodate wing volume, as shown in the last of Figure 3.23. This type of procedure for wing-body shaping is known as the area rule. A smoother distribution of the crosssectional area reduces wave drag.
Whitcomb’s finding was deployed on F102 Delta Dragger fighter aircraft (see Figure 3.23). The modified version with area ruling showed considerably reduced transonic drag (see Figure 4.29). For current designs with wing-body blending, it is less visible, but designers still study the volume distribution to make it as smooth as possible. Even the hump of a Boeing 747 flying close to transonic speed helps with the area ruling. The following subsection considers wing (i. e., 3D body) aerodynamics.
|
|











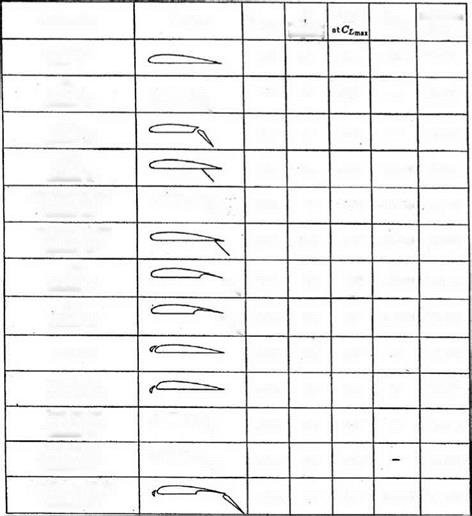
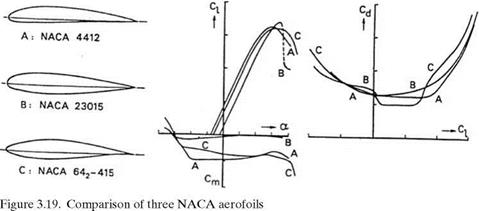
 must choose from a wide variety of aerofoils or generate one suitable for their purposes.
must choose from a wide variety of aerofoils or generate one suitable for their purposes.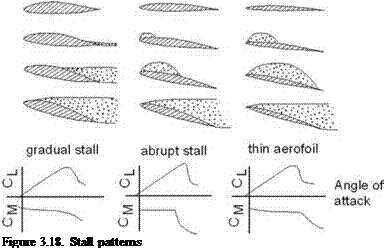
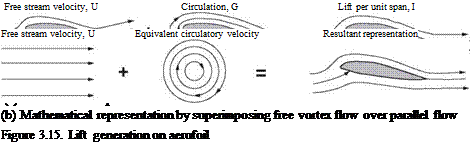
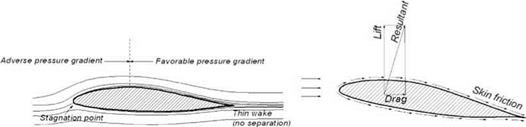
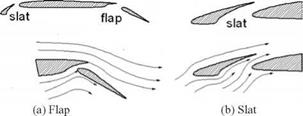
 free streamflow condition and a set of circulatory streamlines of a strength that matches the flow around the aerofoil. The circulatory flow is known as the circulation of the aerofoil. The concept of circulation provides a useful mathematical formulation to represent lift. Circular flow is generated by the effect of the aerofoil camber, which gives higher velocity over the upper wing surface. The directions of the circles show the increase in velocity at the top and the decrease at the bottom, simulating velocity distribution over the aerofoil.
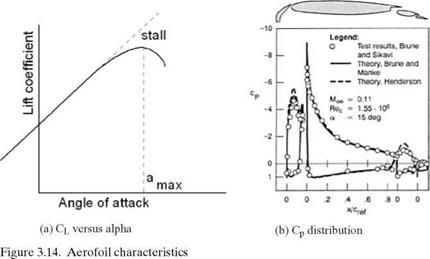
free streamflow condition and a set of circulatory streamlines of a strength that matches the flow around the aerofoil. The circulatory flow is known as the circulation of the aerofoil. The concept of circulation provides a useful mathematical formulation to represent lift. Circular flow is generated by the effect of the aerofoil camber, which gives higher velocity over the upper wing surface. The directions of the circles show the increase in velocity at the top and the decrease at the bottom, simulating velocity distribution over the aerofoil. are ignored in this book), it is noticed that the moment is invariant to the angle of attack until stall occurs. This point at the quarter chord is called the ac, which is a natural reference point through which all forces and moments are defined to act. The ac offers much useful information that is discussed later.
are ignored in this book), it is noticed that the moment is invariant to the angle of attack until stall occurs. This point at the quarter chord is called the ac, which is a natural reference point through which all forces and moments are defined to act. The ac offers much useful information that is discussed later.