Category Aircraft Flight

Now let us return to stronger shock waves across which a noticeable change in flow properties occurs. The changes which take place in the shock wave as the air compresses are extremely rapid, taking place in a distance not much greater than the average distance between impacts of air molecules (approxim­ately 6.6 x 10-5 mm at sea level). Because of this a great deal of the mechanical energy in the flow is converted into thermal energy which is paid for in terms of a large drag force acting on the aerofoil or aircraft. Because this drag is solely associated with the existence of the shock wave systems within the flow, it is known as ‘wave drag’, and one of the main aims in the aerodynamic design of high speed aircraft is the reduction of this drag.

Simple turbo-jet propulsion is inefficient at low speeds, and when high flight speeds are not required, it is better to use the gas turbine to drive a propeller, producing a turbo-prop system, as shown in Fig. 6.20.

In the turbo-prop, most of the energy available in the exhaust gases is extracted by the turbine, and fed to the propeller. Nearly all of the thrust comes from the propeller, rather than directly from the engine as jet propulsion. The turbo-prop, therefore, has a much higher Froude propulsion efficiency than a pure turbo-jet.

The turbo-prop retains many of the advantages and characteristics of turbo­jet propulsion including a high power-to-weight ratio, and a power output that rises with flight speed. Its main disadvantage is that, when used with a conven­tional propeller, it is limited to use at Mach numbers of less than about 0.7.

Because of the high rotational speed of the turbine, turbo-props normally use a reduction gearbox to connect the propeller shaft to that of the turbine. For large engines, the gearbox becomes a very large, heavy and complex item, reducing some of the theoretical advantages of the system.

Despite early scepticism about the economic viability of pure turbo-jet air­craft, the first jet airliner; the De Havilland Comet (Fig. 9.3) started a revolution in air transport when it entered service in May 1952, some two years after the first commercial turbo-prop flights by the Vickers Viscount. It was found that there was no shortage of passengers willing to pay the price premium for a significantly faster service provided by the turbo-jet. The introduction of the bigger, faster and more efficient turbo-jet Boeing 707 in 1958 caused the demise of the large turbo-prop for long-range civil transport, and started the continuing battle to produce ever more efficient jet airliners. The turbo-prop, however, retains a place on shorter routes, where increased speed does not pro­duce such a significant shortening of the overall journey time. The higher cabin noise level of the turbo-prop is also more acceptable on short flights.

Gliding flight is very similar to climbing flight – the main difference being that now we are going down rather than up! The operational requirements are sim­ilar too. We may wish to remain in the air for the maximum possible time, in which case we require the minimum possible rate of descent, or we may wish to travel as far as possible during the glide, in this case it is the minimum angle of glide which is required. Once more we shall find that these two requirements are distinct from each other and the pilot will obtain the minimum sink rate at a different flying speed to the speed at which the minimum sink angle is obtained.

Consideration of the above cases is also very similar to the counterpart in climb. This time, however, we do not have the complication of the engine performance to worry about.

If it is the minimum sink rate that concerns us we merely need to operate at the speed for minimum required power because in gliding flight this must be supplied by loss in the potential energy of the aircraft which is, of course, proportional to the rate of descent (Fig. 7.19).

The argument for minimum glide angle is very similar to that for maximum climb angle. In this case the weight component acting in the direction of flight must exactly balance the drag (Fig. 7.20). This component will be at its small­est when the drag is at a minimum and this condition will correspond to the minimum drag speed.

Weight component in flight direction (balanced by drag)

Fig. 7.20 Minimum glide angle

Minimum glide angle occurs at minimum drag since weight component in direction of motion will then be minimum

Control requirements

An aircraft is free to move in the six different ways illustrated in Fig. 10.1. These are known as the six degrees of freedom, and several aspects of each degree may need to be controlled. For example, we need to be able not only to set the pitch angle, but also to control the rate at which the angle changes. We may even wish to be able to regulate its rate of acceleration, so there can be eighteen or more different aspects to control. To make matters even more complicated, there is often an interaction or cross-coupling between move­ments. As we shall see later, rolling the aircraft invariably causes it to turn (yaw). Since there can be cross-coupling between any pair of factors, there is a large number of possibilities.

With such a vast array of factors to consider, it might seem a daunting task to try to design an aircraft control system. Fortunately, on conventional air­craft, many of the possible cross-coupling effects are insignificant, and can be largely ignored. Traditionally, the important ones were dealt with partly on the basis of experience, and partly by means of simplifications and approxima­tions. Many nicely controllable aircraft were built long before the theoretical design procedures had been fully worked out. Problems always arose, however, when some unconventional configuration was tried, and this led to a very cau­tious attitude to unconventional designs. Very few manufacturers have ever made money out of novel designs, even though they may have benefitted avia­tion in the long term.

Nowadays, it is possible to design very complex control systems with a fair degree of confidence. The most important cross-coupling factors can be predicted, simulated and verified by wind-tunnel experiments, or by test-flying modified aircraft. The introduction of digital electronics into the control sys­tem has made it possible to modify and adjust the control response of the aircraft.

The inherent destabilising effect of a cambered wing section comes from the fact that the centre of lift moves forward with increasing angle of attack. For a tailless aircraft, we could overcome this problem by means of a negatively cam­bered wing section, or a reflex cambered section, as shown in Fig. 11.10. Such sections are rather poor in terms of their lift and drag characteristics, however, and the approach normally used for tailless aircraft is to sweep the wings backward. The wing tips, which are then aft of (behind) the inboard section, are twisted to give a smaller incidence (washout), and take the place of the tail. This principle is employed on many hang-glider designs, and on the powered microlight aircraft derivative shown in Fig. 11.11.

Fig. 11.11 Wing sweep helps to provide both longitudinal and lateral stability on this tailless microlight

The main advantage of a tailless design is that drag-producing junctions between components are reduced. In the Northrop design shown in Fig. 4.19, even the fuselage has been eliminated. For low-speed aircraft, however, the swept tailless type shows little or no significant advantage in terms of drag reduction, as the swept-wing configuration has an inherently lower lift-to-drag ratio than a straight wing. As explained in Chapter 2, for a given wing area, the lift decreases with increasing sweep angle, whereas the drag remains more or less constant, or may even increase. For a transonic aircraft, though, where wing sweep is necessary to reduce compressibility effects, the advantages of the swept tailless configuration might be exploited.

An incidental important feature of all-wing designs such as the Northrop is that the absence of junctions between surfaces makes them relatively poor radar reflectors, thus making them suitable as the basis for development of stealth technology (low detectability).

When a control surface such as an aileron is deflected downwards, the centre of lift moves aft. If the centre of lift under normal conditions is near the flexural centre, then the rearward shift will produce a nose-down twisting moment. The effect of this twisting is to reduce the wing angle of attack, as shown in Fig. 14.3. If the wing is too flexible, the reduction in angle of attack can have a greater effect than the increase in camber, so that the lift decreases instead of

increasing as expected. The consequence is that the control action is reversed, and the aircraft can become virtually impossible to fly.

Such control reversal was sometimes encountered in power-dives, by fast piston-engined aircraft during the Second World War. As we have seen, the centre of lift moves rearwards as the aircraft approaches the speed of sound, so that the possibility of control reversal is increased. The fact that control reversal often occurred as an aircraft approached the speed of sound, led to a belief among pilots that control reversal was an inherent feature of supersonic flight. This is not true. It was simply that the deficiencies in torsional stiffness became critical as the aerodynamic loads and moments increased.

The movement of the centre of lift in high speed flight produces a major design problem, since it is clearly impossible to arrange for the resultant lift force to pass near the flexural centre, in both high and low speed flight cases. The solution is to make the wing sufficiently stiff in torsion (twist), although this may be difficult to achieve without incurring a high weight penalty.

Control reversal occurs mainly with outboard ailerons, and one solution is to use a secondary set in inboard ailerons for high speed flight. The use of spoilers instead of ailerons can provide an alternative solution. The use of slab or all-moving surfaces for control may also help to reduce the problem.

Other static problems

In addition to the rather dramatic cases described above, the flexibility of the aircraft can produce other, sometimes fatal conditions, such as the jamming to control cables, the fracture of hydraulic pipes, and the rupturing of fuel tanks.

For any aircraft wing, conventional or otherwise, lift is generated by producing a greater pressure under the wing than above it. To produce this pressure difference, all that is required is a surface that is either inclined to the relative air flow direction as shown in Fig. 1.4, or curved (cambered) as in Fig. 1.5. In practice, it is normal to use a combination of inclination and camber. The cross-sectional profiles shown in Figs 1.4 and 1.5 have all been used on suc­cessful aircraft. The shape used for a particular aircraft depends mainly on its speed range and other operational requirements.

The problem is to explain why such shapes produce a pressure difference when moved through the air. Early experimenters found that whether they used a curved or an inclined surface, the average speed of air flow relative to the wing was greater on the upper surface than on the underside. As we shall see later, increases in air flow speed are associated with a reduction in pressure, so the lower pressure on the upper surface is associated with the higher relative air speed. Explanations for the generation of lift are, therefore, often based on the idea that the difference in speed between upper and lower surfaces causes the difference in pressure, which produces the lift. These explanations are, however, unconvincing, because, as with the chicken and the egg, we might alternatively argue that the difference in pressure causes the difference in speed. It is also difficult to explain in simple physical terms why the difference in speed occurs.

One popular and misleading explanation refers to a typical cambered wing section profile such as that shown in Fig. 1.5(a). It is argued, that the air that takes the longer upper-surface route has to travel faster than that which takes the shorter under-surface route, in order to keep up.

Apart from the fact that it is not obvious why the flows over the upper and lower surfaces should have to keep in step, this explanation is unsatisfactory. Inclined flat-plate, or symmetrical-section wings, where the upper and lower

surfaces are the same length, lift just as well as cambered (curved) ones. Also, the cambered profile of Fig. 1.5(a) will still lift even if turned upside down, as in Fig. 1.5(d), as long as it is inclined to the flow direction. Anyone who has ever watched a flying display will be aware that many aircraft can be flown upside down. In fact, there is no aerodynamic reason why any aircraft cannot be flown inverted. The restrictions imposed on this kind of manoeuvre are mainly due to structural considerations.

Almost any shape will generate lift if it is either cambered or inclined to the flow direction. Even a brick could be made to fly by inclining it and propelling it very fast. A brick shape is not the basis for a good wing, but this is mainly because it would produce a large amount of drag in relation to the amount of lift generated.

If you study the flow around any of the inclined or cambered sections illus­trated in Figs 1.4 and 1.5, you will find that the air always does go faster over the upper surface. Furthermore, it does take a longer path over the top surface. The unexpected way in which it contrives to do this is shown in Fig. 1.6(a) (and Fig. 1.13). It will be seen that the flow divides at a point just under the nose or leading edge, and not right on the nose as one might have expected. The air does not take the shortest possible path, but prefers to take a rather tortuous route over the top, even flowing forwards against the main stream direction for a short distance.

It is clear that the generation of lift does not require the use of a conven­tional aerofoil section of the type shown in Fig. 1.5(a), and any explanation entirely based on its use is unsatisfactory.

We find that the production of lift depends, rather surprisingly, on the vis­cosity or stickiness of air. Early theories that ignored the viscosity, predicted that the flow patterns around a simple inclined surface would take the form illustrated in Fig. 1.6(b). You will see that in this diagram, there is a kind of symmetry to the pattern of streamlines. They would look exactly the same if you turned the page upside-down. There is, therefore, a similar symmetry in the pressure distribution, so that there must be exactly corresponding areas of low and high pressure on the upper and lower surfaces. Consequently, no lift would be produced.

In reality, the flow patterns are like those shown in Fig. 1.6(a). The import­ant difference is that here the upper and lower surface flows rejoin at the trailing edge, with no sudden change of direction. There is no form of sym­metry in the flow. There is a difference in the average pressure between upper and lower surfaces, and so lift is generated.

This feature of the flows meeting at the trailing edge is known as the Kutta condition. In Chapter 3 we describe how the viscosity (the stickiness) of the air causes this asymmetrical flow, and is thus ultimately responsible for the production of lift.

The theory of vortex behaviour that predicted a closed circuit also indicates that a steady vortex cannot vary in strength along its length. However, it was soon found that real wings do not generally produce the same amount of lift per metre of span at the centre as they do at the tips, so the horseshoe vortex system shown in Fig. 2.3 is clearly an over-simplification.

The solution proposed by Lanchester, is to imagine a whole series of horse­shoe vortex lines or ‘filaments’, as shown in Fig. 2.10. At the centre of the wing,

where the lift per metre of span is greatest, there is the largest number of vortex lines. If you refer back to Fig. 2.6(b), you will see that just downstream of the wing trailing edge, there is a rotational tendency or vorticity across the whole of the span, even though it only forms a clearly defined vortex near the tips. By making horseshoe vortex shapes of different spans, we can represent the way that vorticity is shed all along the span. In Fig. 2.10, we show how this vorticity wraps up into a single pair of well defined trailing vortices.

The fact that the rotational tendency occurs all along the wing, just down­stream of the trailing edge, rather than only at the tips, ties up with the phys­ical behaviour shown in Fig. 2.6.

Figure 2.10 is similar to the diagram originally given by Lanchester in 1897. Unfortunately, his ideas were not immediately understood, and they were not published until 1907. Lanchester was not good at describing his work in clear language, and he had a habit of making it sound bogus by inventing pompous words such as phugoid (which we shall encounter later) and aerofoil!

The German engineer Ludwig Prandtl, who had been working along similar lines, developed these ideas into a usable mathematical model. The so-called Lanchester-Prandtl theory represented a major breakthrough in the under­standing of aircraft flight. It also forms the basis of mathematical theories in which the wing-bound and trailing vorticity are represented by a large array of vortex lines or rings. Although we are not concerned with mathematics in this book, the concepts involved in the Lanchester-Prandtl theory can be helpful to our appreciation of the physical principles of aircraft aerodynamics.

In order to reduce the boundary layer normal pressure drag, it is important to ensure that the pressure gradient is not strongly adverse, which means that the

Circular rod producing the same amount of drag

tail of the body should reduce in depth or cross-sectional area gradually. This leads to the classical streamlined shape shown in Fig. 4.3.

The worst possible shape in terms of normal pressure drag, is a blunt object with sharp corners, since separation will occur at the corners, leaving a low pressure over the whole of the rear.

The advantages of streamlining

The streamlined shape shown in Fig. 4.3 is a symmetrical aerofoil and at zero angle of attack it has a drag coefficient of around 0.03 based on frontal area (0.005 based on plan area). This may be compared with the drag coefficient of a circular cylinder which is 0.6 (at a Reynolds number of 6 x 106). This means, that a circular rod would produce 20 times as much drag as the streamlined section of the same depth. Looking at it another way, a 5 mm diameter wire would produce as much drag as a streamlined fairing 100 mm deep. We can, therefore, see why it was so necessary to eliminate the external bracing wires used on vintage aircraft.

When the aircraft shown in Fig. 6.3 start moving, the useful power is the product of the thrust and the aircraft speed. We can therefore define a form of propulsive efficiency as the ratio:

the useful power

the useful + the rate at which energy is used to increase power the kinetic energy in the slipstream or jet

This is known as the Froude efficiency.

Thrust = 50 x 80 = 4000 N

Energy rate = 50 x 80 = 160 000 W

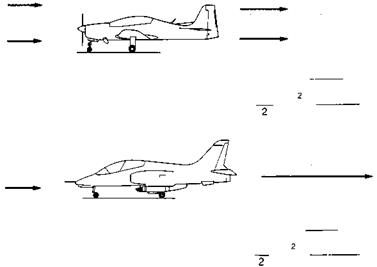
Fig. 6.3 Static thrust production by a propeller and jet compared

The large disc area of the propeller enables it to work on a larger mass of air per second, but with a lower slipstream or jet velocity than the jet-engined aircraft. Although the two aircraft are producing the same thrust, the jet-engined aircraft is transferring energy to the slipstream five times faster, so it needs to burn fuel at a much higher rate

From the discussions above, we can see that the Froude efficiency will be higher for the propeller-driven aircraft at any given speed and thrust since it is trans­ferring energy to the air at a lower rate.

Froude efficiency improves with flight speed for both jet and propeller – driven aircraft, but if it were not for compressibility problems, propeller propulsion would always have the higher Froude efficiency at any particular speed and thrust. As we shall show, at high speeds, this theoretical advantage of the propeller is extremely difficult to realise in practice.

From the example of the propeller and jet-propelled aircraft given above we can see that, for efficient propulsion, it is better to generate thrust by giving a small change of velocity to a large mass of air, than by giving a large change in velocity to a small mass. The proof of this may be found in Houghton and Carpenter (2003). In simple terms, it arises because thrust per kilogram of air is related to the change in air velocity whereas relative energy expenditure rate depends on the change in the square of the velocity.

Of all the propulsion systems currently employed, propeller systems are potentially the most efficient, since they involve relatively large masses of air and small velocity changes. Pure jet engines are inherently less efficient, because, for an equal amount of thrust, they use much larger changes of velo­city, and smaller masses of air.

It is interesting to note that one of the most theoretically efficient propulsion systems so far devised is the flapping wing of a bird, since this utilises the maximum possible area, and hence the largest air mass for a given overall dimension. Helicopters have a similar theoretical advantage, although in prac­tice, technical problems have always resulted in their being rather inefficient. This raises the important point that the best propulsion system is the one that can be made to work most efficiently in practice.

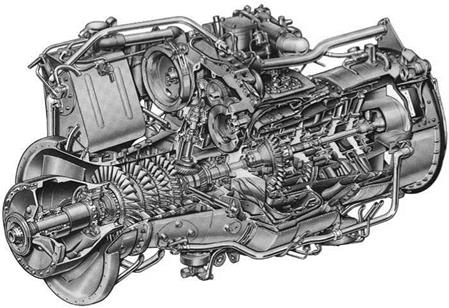
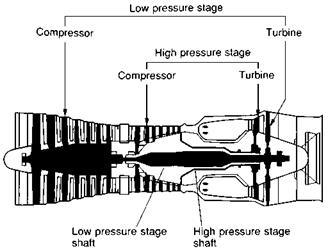
The Froude efficiency defined above, is only one aspect of the efficiency of propulsion. We have to consider the efficiency of each stage of the energy conversion process. In a simple turbo-jet engine, power is produced by adding energy to the air stream by direct heating, which can eliminate some of the intermediate steps of a propeller system. Many other factors, such as the amount of thermal energy thrown out with the exhaust, contribute to the over­all inefficiency. We shall discuss these contributions later in our more detailed descriptions of particular propulsion devices.

Although the Froude efficiency of the turbo-jet may be lower than that of a propeller system, it has the advantage that there is virtually no limit to the speed at which it can be operated, and it works well at high altitude. The ratio of power to weight can also be very high for jet engines.

One of the most important requirements for efficient propulsion, is to ensure that all of the components, including the aircraft itself, produce a high effi­ciency at the same design operating condition. The correct matching of aircraft and powerplant is of major importance. In many cases, a new engine must be designed, or an old one extensively modified, to meet the needs of the new aircraft design. As we shall see later, compromises often have to be made, and in some cases we need to sacrifice efficiency in the interests of other considera­tions, such as high speed, or low capital cost.