4.1 General Background of Flexible Wing Flyers
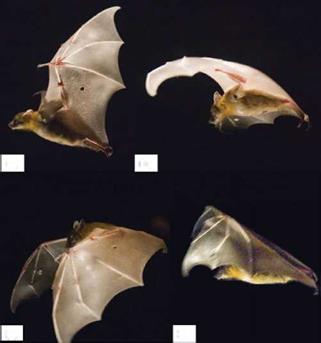
As discussed in Section 1.1, it is well known that flying animals typically have flexible wings to adapt to the flow environment. Birds have different layers of feathers, all of which are flexible and often connected to each other. Hence, they can adjust the wing planform for a particular flight mode. Furthermore, bats have more than two dozen independently controlled joints in the wing [400] and highly deforming bones [401] that enable them to fly at either positive or negative AoAs, to dynamically change wing camber, and to create complex 3D wing topology to achieve extraordinary flight performance. Bats have compliant thin-membrane surfaces, and their flight is characterized by highly unsteady and 3D wing motions (see Fig. 4.1).
As discussed in Chapter 1, birds and bats can also change their wingspan (flexing their wings) to decrease the wing area, increase the forward velocity, or reduce drag during an upstroke. In fast forward flight, birds and bats reduce their wing area slightly during the upstroke relative to the downstroke. At intermediate flight speeds, the flexion during the upstroke becomes more pronounced. However, bats and birds flex their wings in different manners. The wing surface area of a bird’s wing consists mostly of feathers, which can slide over each other as the wing is flexed and still maintain a smooth surface. Bat wings, in contrast, are mostly a thin membrane supported by the arm bones and the enormously elongated finger bones. Given the stretchiness of the wing membrane, bats can flex their wings a little, reducing the span by about 20 percent, but they cannot flex their wings too much or the wing membrane will go slack. Slack membranes are inefficient, because drag goes up and the trailing edges are prone to flutter, making them harder for fast flight [22].
While making bending or twisting movements, biological flyers have natural capabilities of adjusting the camber of their wings in accordance with what the flow environment dictates, such as a wind gust, object avoidance, and target tracking. Bats are known for being able to change the shape of the wing passively, depending on the free-stream conditions. As shown in Figure 4.1 bats can change their wing shapes during each flapping cycle. In human-made devices, sails and parachutes operate according to similar concepts. This passive control of the wing surface can prevent flow separation and enhance lift-to-drag ratio. Birds adjust their wings based on different strategies. For example, some species have coverts that act as self-activated

 (d)
(d)
Figure 4.1. A bat (Cynopterus brachyotis) in flight. (a) Beginning of downstroke, head forward, tail backward: the whole body is stretched and lined up in a straight line. (b) Middle of downstroke: the wing is highly cambered. (c) End of downstroke (also beginning of upstroke): the wing is still cambered. A large part of the wing is in front of the head and the wing is going to be withdrawn to its body. (d) Middle of upstroke: the wing is folded towards the body. FromTian et al. [231].
flaps to prevent flow separation. These features offer shape adaptation and help adjust the aerodynamic control surfaces; they can be especially helpful during landing and in an unsteady environment. In Figure 4.2 the coverts have popped up on a skua, and the flexible structure of the feathers is clearly shown. Figure 4.3 highlights three flyers in different flight modes: an egret fishing, a kingfisher trying to land, and a Black Kite during cruising.
Insect wings deform to a great extent during flight, and their wing properties are generally anisotropic because of the membrane-batten structures; the spanwise bending stiffness is about 1 to 2 orders of magnitude larger than the chordwise bending stiffness in a majority of insect species. Experimental efforts reported a scaling relationship between wing flexural stiffness and wing length scale [402] [ 403]. In Combes and Daniel’s analysis each flexural stiffness is estimated based on a 1D beam model. The results showed that spanwise flexural stiffness scales with the third power of the wing chord, whereas the chordwise stiffness scales with the second power of the wing chord [402]. Figure 4.4 shows wings of cardinals, hummingbirds, bats, dragonflies, cicadas, and wasps, all exhibiting similar overall structural characteristics. They exhibit substantial variations in ARs and shapes, but share a common feature of a reinforced leading edge. A dragonfly wing has more local variations in its structural composition and is more corrugated than the wing of a cicada or a wasp. It was shown in the literature that wing corrugation increases both warping rigidity
|

Figure 4.2. The flexible covert feathers acting like self-activated flaps on the upper wing surface of a skua. Photo from Bechert et al. [416].
|
and flexibility [24]. The wing structure of a dragonfly helps prevent fatigue fracture [24].
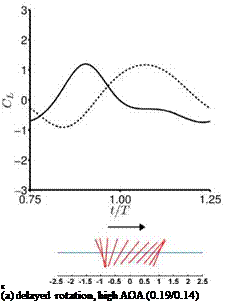
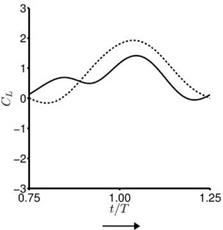
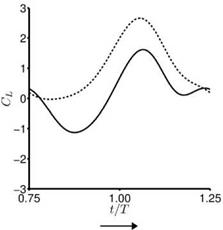
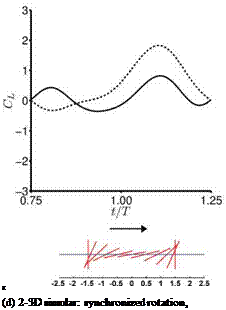
Moreover, wing flexibility can allow for a passive pitching motion due to the inertial forces during the wing rotation as the stroke reverses [303]. There are three modes of passive pitching motion that are similar to those considered in the studies of rigid wing models (see also Fig. 3.9) [201] [245] [301]: (i) delayed pitching, (ii) synchronized pitching, and (iii) advanced pitching. The ratio of flapping frequency to the natural frequency of the wing is key to determining the modes of the passive pitching motion of the wing [404]. The thin nature of the insect wing skin structure makes it unsuitable for taking compressive loads, which may result in skin wrinkling and/or buckling. On the aerodynamics side, for example, wind-tunnel measurements show that corrugated fixed wings are aerodynamically insensitive to the Reynolds number variations, which is quite different from a typical low Reynolds number airfoil (see Section 3.5). For example, Figure 2.5 shows that a dragonfly wing is insensitive to the variation of the Reynolds number in its operating range, in contrast to the Eppler 374 airfoil, which displays a zigzag pattern at a certain Reynolds number range. Obviously, these features go beyond the fact that, as a flyer’s size is reduced, the wing becomes thinner and tends to become more flexible. As discussed in detail, the flexibility of the wing has a profound impact on its performance in lift, drag, and thrust. Fundamentally, a passively compliant structure can help adjust the structures so that the resulting aerodynamics can remain desirable [405]-[408]. Realizing that the dimensionless scaling of both fluid dynamics and structural dynamics (and their interactions) cannot be invariant, instead of trying to map out all physical mechanisms versus different Reynolds numbers and sizes, frequencies, and the like, one needs to focus on identifying favorable combinations of materials (elasticity, anisotropy, spatially varying properties, and so on) and on controlling the shape deformation of combined flapping and flexible structural dynamics, with the goal of identifying the most optimized combination of the kinematics, structural behavior, and possible control strategies (including hovering and wind gust effects).
|

Figure 4.3. Flexible wing patterns of three flyers in different flight modes, including an egret as a predator, a kingfisher trying to land, and a Black Kite during cruising.
|
Overall, biological flyers have several outstanding features that may pose several design challenges in the design of MAVs. For example, (i) there is substantial anisotropy in the wing structural characteristics between the chordwise and spanwise directions; (ii) they employ shape control to accommodate spatial and temporal flow structures; (iii) they accommodate wind gust and accomplish station keeping with varying kinematics patterns; (iv) they use multiple unsteady aerodynamic mechanisms for lift and thrust enhancement; and (v) they combine sensing, control, and wing maneuvering to maintain not only lift but also flight stability. In principle, one might like to first understand these biological systems, abstract certain desirable features, and then apply them to MAV design. A challenge is that the scaling of fluid dynamics, structural dynamics, and flight dynamics between smaller natural flyers and practical flying hardware/lab experiments (larger dimension) is fundamentally difficult. Regardless, to develop a satisfactory flyer, one needs to meet the following objectives:
• Generate necessary lift, which scales with the vehicle/wing length scale as L3ef (under geometric similitude); however, often, a flyer needs to increase or reduce lift to maneuver toward/avoid an object, resulting in the need for substantially more complicated considerations
• Minimize power consumption
 Bat
Bat
Wasp
Cardinal
Cicada
Hummingbird
Dragonfly
Figure 4.4. Flexible and selectively stiffened wings of a cardinal, hummingbird, bat, dragonfly, cicada, and wasp.
As illustrated in Section 1.1, when wind gust adjustment, object avoidance, or station keeping become major factors, highly deformed wing shapes and coordinated wing – tail movement are often observed (see Fig. 1.12). Understanding of the aerodynamic, structural, and control implications of these modes is essential for the development of high-performance and robust MAVs capable of performing desirable missions. The flexibility of animal wings leads to complex fluid-structure interactions, whereas the kinematics of flapping and the spectacular maneuvers performed by natural flyers result in highly coupled non-linearities in fluid mechanics, aeroelasticity, flight dynamics, and control systems. Can large flexible deformations provide a better interaction with the aerodynamics than those limited to the linear regimes? If torsion stiffness along the wingspan can be tailored, how does that affect the wing kinematics for optimum thrust generation? How do these geometrically non-linear effects and the anisotropy of the structure affect the aerodynamics characteristics of the flapping wing?
Interaction between air and a thin structure is not only observed in animal locomotion. For example, the lift enhancement due to LEV formation that is discussed in the context of unsteady aerodynamic mechanisms in Chapter 3 is observed for autorotating plant seeds [409]. Freely falling papers [410] and their characteristic rotations that are typical for business cards or leafs [411] [412] are also well modeled with the principles described in Chapter 3. More recently, deformations of a leaf and the flow field around it have been measured at different wind speeds in a wind tunnel [413] (see also Fig. 4.5). The leafs reconfigure themselves by streamlining their structure such that the resulting drag grows slower than the classical U2
Figure 4.5. Six-inch (15-cm) MAV with flexible wing; from Ifju et al. [17].
 relations [414]. The vibration of the trees due to strong wind is one of the main reasons why trees are damaged, and uncovering these daily life physics helps us meet our environmental challenges.
relations [414]. The vibration of the trees due to strong wind is one of the main reasons why trees are damaged, and uncovering these daily life physics helps us meet our environmental challenges.
Nature’s design of flexible structures can be put into practice for MAVs. Adopting a flexible wing design (see Figs. 4.6 and 4.7) similar to bat wings can improve the performance of MAVs, especially at high AoAs by passive shape adaptation, which results in delayed stall [147] [ 406]. Figure 4.8, adapted from Waszak et al. [406], compares the lift curves versus AoAs for rigid and membrane wings. The three different flexible wing arrangements are depicted in Figure 4.7. The one-batten design has the most flexibility characterized by large membrane stretch. The two-batten design is, by comparison, stiffer and exhibits less membrane stretch under aerodynamic load. The six-batten wing is covered with an inextensible plastic membrane that further increases the stiffness of the wing and exhibits less membrane deformation and vibration. The nominally rigid wing is constructed with a two-batten frame covered with a rigid graphite sheet. Under modest AoA, both rigid and membrane wings demonstrate similar lift characteristics, with the stiffer wings having a slightly higher lift coefficient. However, a membrane wing stalls at a substantially higher AoA than a rigid wing. This aspect is a key element in enhancing the stability and agility of MAVs.
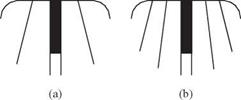 Figure 4.6. Three versions of the flexible wing were tested in the wind tunnel; from Waszak et al. [406]. (a) One-batten flexible wing; (b) two-batten flexible wing; and (c) six-batten flexible wing covered with an plastic inextensible membrane.
Figure 4.6. Three versions of the flexible wing were tested in the wind tunnel; from Waszak et al. [406]. (a) One-batten flexible wing; (b) two-batten flexible wing; and (c) six-batten flexible wing covered with an plastic inextensible membrane.
(c)
(b) Smoke-wire visualation of the flow behind a leaf at the AoA of 90°.
Figure 4.7. Aeroelastic study of a leaf in controlled laboratory setting. From Shao et al. [413].
|

Figure 4.9. Representative MAVs with membrane wing developed by Peter Ifju and collaborators at the University of Florida. Left: the wing is framed along the entire peripherals. Right: the wing is flexible along the trailing edge while reinforced by battens.
|
The membrane concept has been successfully incorporated in MAVs designed by Ifju et al. [17] and Stanford et al. [407]. However, traditional materials such as balsawood, foam, and monocoat, are not appropriate for implementing the flexible wing concept on these small vehicles. In their design illustrated in Figure 4.6 and Figure 4.9, unidirectional carbon fiber and cloth prepreg materials are used for the skeleton (leading-edge spar and chordwise battens). These are the same materials used for structures that require fully elastic behavior yet undergo large deflections. The fishing rod is a classic example of such a structure. For the membrane, extensible material is chosen to allow for deformations even under very small loads, such as for lightly loaded wings. Latex rubber sheet material has been used in this case. The stiffness of the whole structure can be controlled by the number of battens and the membrane material used.
As presented earlier, the experimental data for rigid and flexible wings (Fig. 4.8), with configurations similar to that shown in Figure 4.9, show that a membrane wing stalls at a substantially higher AoA than a rigid wing. Some aspects of low AR, low Reynolds number, and rigid wing aerodynamics have been presented by Torres and Mueller [162] as well as in Chapter 2. The lift-curve slope in Figure 4.8 is approximately 2.9 with the prop pinned. The lift-curve slopes of similar rigid wings reported by Torres and Mueller [162] at a comparable Reynolds number and aspect ratio (Re = 7 x 104, AR = 2) are approximately 2.9 as well. However, these wings have stall angles between 12° and 15°. The stall angles of the flexible wings are between 30° and 45° and are similar to those of much lower aspect ratio rigid wings (AR = 0.5 to 1.0) [159]. However, low-aspect-ratio rigid wings exhibit noticeably lower lift-curve slopes, typically between 1.3 and 1.7 [159]. Hence, flexible wings can effectively maintain the desirable lift characteristics with better stall margins [406]. Figure 4.8 shows fixed, flexible-wing MAVs designed by Ifju and co-workers of the University of Florida [17]. The general specifications of the design are presented in Table 4.1. Stanford et al. [407] and Shyy et al. [408] reviewed the development of membrane-based fixed wing MAVs.
Figure 4.10. The flexible wing allows for wing warping to enhance vehicle agility [415].
 From an engineering point of view, flexibility can be used for purposes other than flight quality improvement. These objectives include shape manipulation and reconfiguration for both improved maneuvering and storage. Traditional control surfaces such as rudders, elevators, and ailerons have been used almost exclusively for flight control. By morphing or reshaping the wing using distributed actuation such as piezoelectric and shape memory material, preferred wing shapes can be developed for specific flight regimes. Such reconfiguration, however, would require substantial authority and power if the wings are nominally rigid. The flexible nature of the wing allows for such distributed actuation with orders of magnitude less authority. For example, the individual battens on the wing can be made from shape memory alloys, piezoelectric materials, or traditional actuators, such as servos, which can be used to manipulate the shape and properties of the wing.
From an engineering point of view, flexibility can be used for purposes other than flight quality improvement. These objectives include shape manipulation and reconfiguration for both improved maneuvering and storage. Traditional control surfaces such as rudders, elevators, and ailerons have been used almost exclusively for flight control. By morphing or reshaping the wing using distributed actuation such as piezoelectric and shape memory material, preferred wing shapes can be developed for specific flight regimes. Such reconfiguration, however, would require substantial authority and power if the wings are nominally rigid. The flexible nature of the wing allows for such distributed actuation with orders of magnitude less authority. For example, the individual battens on the wing can be made from shape memory alloys, piezoelectric materials, or traditional actuators, such as servos, which can be used to manipulate the shape and properties of the wing.
Figure 4.10 illustrates a model with morphing technology. It employs a thread connecting the wingtips to a servo in the fuselage of the airplane. As the thread is tightened on one side of the aircraft, it acts like an aileron and causes the AoA of the wing to increase. The roll rate developed by such an actuation mechanism is considerably higher than that from a rudder. Additionally, it produces nearly pure roll with little yaw interaction. Detailed information on the related technical approaches has been presented by Garcia et al. [415].
In some applications, it is desirable to store MAVs in small containers before releasing them. Flexible wing MAVs can be easily reconfigured for storage purposes. Figure 4.11 illustrates a 28 cm (11 inch) wingspan foldable wing MAV that can be
Figure 4.11. A foldable wing to enhance MAV portability and storage (Courtesy Peter Ifju).
 stored in a 7.6 cm (3 inch) diameter canister. The wing uses a curved shell structural element on the leading edge, which enables the wing to readily collapse downward for storage, yet maintain rigidity in the upward direction to react to the aerodynamic loads. The effect is similar to that of a common tape measure, where the curvature in the metallic tape is used to retain the shape after it has unspooled from the casing, yet it can be rolled back into the casing to accommodate the small-diameter spool. The curvature ensures that the positive (straight) shape is developed after it is unwound from the case and can actually be cantilevered for some distance. The curvature of the leading edge of the wing acts as the curvature in the tape measure.
stored in a 7.6 cm (3 inch) diameter canister. The wing uses a curved shell structural element on the leading edge, which enables the wing to readily collapse downward for storage, yet maintain rigidity in the upward direction to react to the aerodynamic loads. The effect is similar to that of a common tape measure, where the curvature in the metallic tape is used to retain the shape after it has unspooled from the casing, yet it can be rolled back into the casing to accommodate the small-diameter spool. The curvature ensures that the positive (straight) shape is developed after it is unwound from the case and can actually be cantilevered for some distance. The curvature of the leading edge of the wing acts as the curvature in the tape measure.











 (d)
(d)

 Bat
Bat relations [414]. The vibration of the trees due to strong wind is one of the main reasons why trees are damaged, and uncovering these daily life physics helps us meet our environmental challenges.
relations [414]. The vibration of the trees due to strong wind is one of the main reasons why trees are damaged, and uncovering these daily life physics helps us meet our environmental challenges. Figure 4.6. Three versions of the flexible wing were tested in the wind tunnel; from Waszak et al. [406]. (a) One-batten flexible wing; (b) two-batten flexible wing; and (c) six-batten flexible wing covered with an plastic inextensible membrane.
Figure 4.6. Three versions of the flexible wing were tested in the wind tunnel; from Waszak et al. [406]. (a) One-batten flexible wing; (b) two-batten flexible wing; and (c) six-batten flexible wing covered with an plastic inextensible membrane.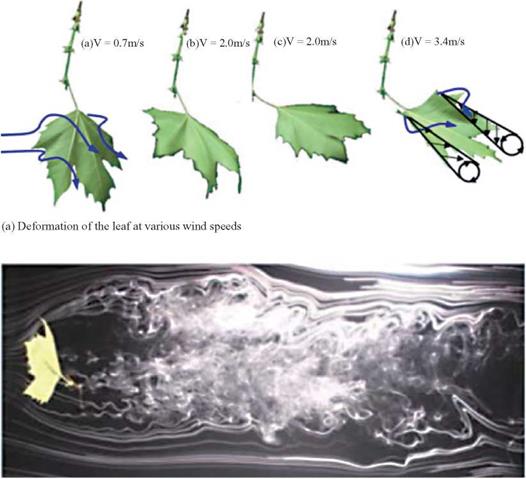
![Подпись: -•— Rigid (Graphite) Figure 4.8. Aerodynamic parameters vs. angle of attack for configurations with varying wing stiffness: (a) lift coefficient versus angle of attack; (b) lift-to-drag ratio versus the angle of attack. From Waszak et al. [406].](/img/3131/image366_2.gif)

 From an engineering point of view, flexibility can be used for purposes other than flight quality improvement. These objectives include shape manipulation and reconfiguration for both improved maneuvering and storage. Traditional control surfaces such as rudders, elevators, and ailerons have been used almost exclusively for flight control. By morphing or reshaping the wing using distributed actuation such as piezoelectric and shape memory material, preferred wing shapes can be developed for specific flight regimes. Such reconfiguration, however, would require substantial authority and power if the wings are nominally rigid. The flexible nature of the wing allows for such distributed actuation with orders of magnitude less authority. For example, the individual battens on the wing can be made from shape memory alloys, piezoelectric materials, or traditional actuators, such as servos, which can be used to manipulate the shape and properties of the wing.
From an engineering point of view, flexibility can be used for purposes other than flight quality improvement. These objectives include shape manipulation and reconfiguration for both improved maneuvering and storage. Traditional control surfaces such as rudders, elevators, and ailerons have been used almost exclusively for flight control. By morphing or reshaping the wing using distributed actuation such as piezoelectric and shape memory material, preferred wing shapes can be developed for specific flight regimes. Such reconfiguration, however, would require substantial authority and power if the wings are nominally rigid. The flexible nature of the wing allows for such distributed actuation with orders of magnitude less authority. For example, the individual battens on the wing can be made from shape memory alloys, piezoelectric materials, or traditional actuators, such as servos, which can be used to manipulate the shape and properties of the wing. stored in a 7.6 cm (3 inch) diameter canister. The wing uses a curved shell structural element on the leading edge, which enables the wing to readily collapse downward for storage, yet maintain rigidity in the upward direction to react to the aerodynamic loads. The effect is similar to that of a common tape measure, where the curvature in the metallic tape is used to retain the shape after it has unspooled from the casing, yet it can be rolled back into the casing to accommodate the small-diameter spool. The curvature ensures that the positive (straight) shape is developed after it is unwound from the case and can actually be cantilevered for some distance. The curvature of the leading edge of the wing acts as the curvature in the tape measure.
stored in a 7.6 cm (3 inch) diameter canister. The wing uses a curved shell structural element on the leading edge, which enables the wing to readily collapse downward for storage, yet maintain rigidity in the upward direction to react to the aerodynamic loads. The effect is similar to that of a common tape measure, where the curvature in the metallic tape is used to retain the shape after it has unspooled from the casing, yet it can be rolled back into the casing to accommodate the small-diameter spool. The curvature ensures that the positive (straight) shape is developed after it is unwound from the case and can actually be cantilevered for some distance. The curvature of the leading edge of the wing acts as the curvature in the tape measure.
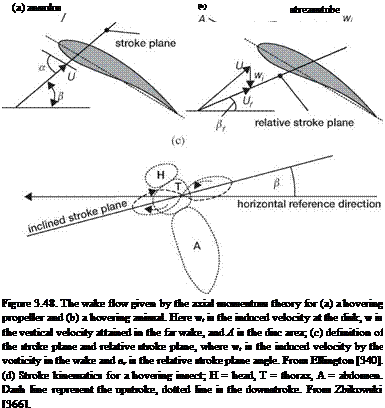
 Figure 3.62. Hovering Japanese White-eye wake flow fields on a frontal plane. Color contours represent the vorticity distribution of the flow fields. (a-c) Near-wake flow fields pertaining to kinematic phases of the ventral clap; purple patches mark the position of the two wings, and purple dotted lines indicate an outline of the bird. (d) The far-wake flow field beneath a hovering Japanese White-eye after phase 3; thick red arrows depict the trends of the flow motion. (a-d) Thick red arrows show the trends of flow motions. (e) Schematic sketches summarizing the wake flow structures for the three kinematic phases. Black arrows indicate fluid jets; orange and blue spiral arrows represent, respectively, the LEV and TEV. Purple arrows signify the downward jet generated by the downstroking wings executing the ventral clap. From Chang et al. [391].
Figure 3.62. Hovering Japanese White-eye wake flow fields on a frontal plane. Color contours represent the vorticity distribution of the flow fields. (a-c) Near-wake flow fields pertaining to kinematic phases of the ventral clap; purple patches mark the position of the two wings, and purple dotted lines indicate an outline of the bird. (d) The far-wake flow field beneath a hovering Japanese White-eye after phase 3; thick red arrows depict the trends of the flow motion. (a-d) Thick red arrows show the trends of flow motions. (e) Schematic sketches summarizing the wake flow structures for the three kinematic phases. Black arrows indicate fluid jets; orange and blue spiral arrows represent, respectively, the LEV and TEV. Purple arrows signify the downward jet generated by the downstroking wings executing the ventral clap. From Chang et al. [391].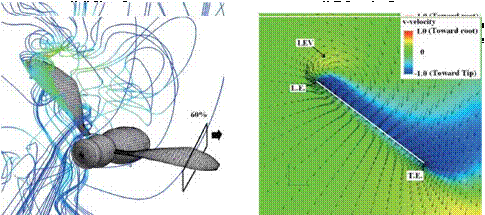



 Doughnut-shaped vortex ring
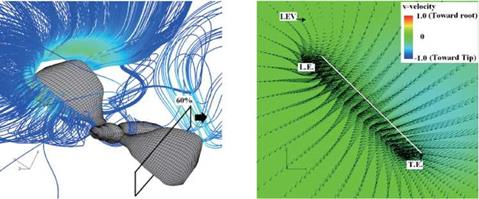
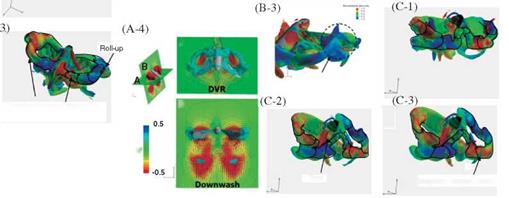
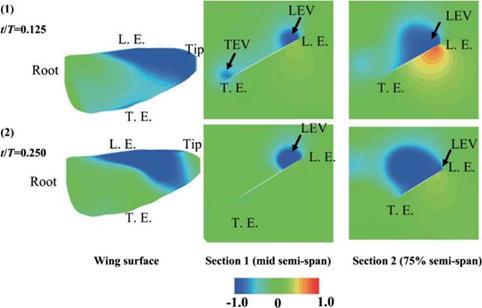
Doughnut-shaped vortex ring in Fig. 3.57). As expected, coherent LEVs, TEVs, and TiVs together enhance the lift generation in hovering flight of the hawkmoth. During the mid-downstroke (see point (c) in Fig. 3.57), the TEVs shed mostly from the wings while on the body they stay attached. Moreover, the shed TEVs stay connected to the TiVs (Fig. 3.58A-2). Overall, the LEVs produce the largest and strongest area of low pressure on the wing surface (Fig. 3.61, section 2). Shortly afterward, the LEVs begin to break down at a location approximately 70-80 percent the span of the wing length. At the same time, the LEV, the TiV, and the shed TEV together form a doughnut-shaped vortex ring around each wing (Fig. 3.58A-3). Similar vortex ring structures have been observed around a hovering hummingbird [261] [266], a bat in slow forward flight [268], and a free-flying bumble bee [259]. During the second half of the downstroke (see point (d) in Fig. 3.57), the TiVs enlarge and weaken. As the wings approach the end of the downstroke, both LEVs and TiVs begin to detach from the wings. During most of the downstroke, the doughnut-shaped vortex ring pair has an intense, downward jet flow through the “doughnut” hole, which forms the downstroke downwash (see Fig. 3.58A-4).
in Fig. 3.57). As expected, coherent LEVs, TEVs, and TiVs together enhance the lift generation in hovering flight of the hawkmoth. During the mid-downstroke (see point (c) in Fig. 3.57), the TEVs shed mostly from the wings while on the body they stay attached. Moreover, the shed TEVs stay connected to the TiVs (Fig. 3.58A-2). Overall, the LEVs produce the largest and strongest area of low pressure on the wing surface (Fig. 3.61, section 2). Shortly afterward, the LEVs begin to break down at a location approximately 70-80 percent the span of the wing length. At the same time, the LEV, the TiV, and the shed TEV together form a doughnut-shaped vortex ring around each wing (Fig. 3.58A-3). Similar vortex ring structures have been observed around a hovering hummingbird [261] [266], a bat in slow forward flight [268], and a free-flying bumble bee [259]. During the second half of the downstroke (see point (d) in Fig. 3.57), the TiVs enlarge and weaken. As the wings approach the end of the downstroke, both LEVs and TiVs begin to detach from the wings. During most of the downstroke, the doughnut-shaped vortex ring pair has an intense, downward jet flow through the “doughnut” hole, which forms the downstroke downwash (see Fig. 3.58A-4).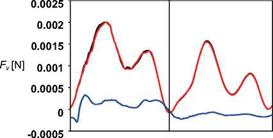
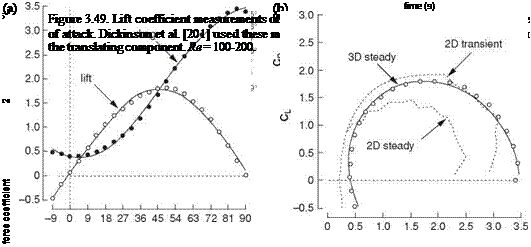
![Подпись: Figure 3.56. A morphological model of a hawk- moth, Agrius convolvuli, with a computational model superimposed on the right half. The hawk- moth has a body length of 5.0 cm, a wing length of 5.05 cm (mean wing chord length cm = 1.83 cm), and an aspect ratio of 5.52. The image is from Aono, Shyy, and Liu [384].](/img/3131/image333_3.gif)
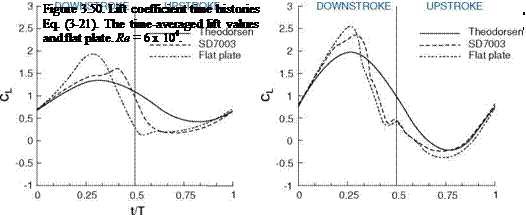
 profiles with low accelerations affect the timing and the magnitude of the lift peak, but at higher accelerations, the velocity profile is insignificant.
profiles with low accelerations affect the timing and the magnitude of the lift peak, but at higher accelerations, the velocity profile is insignificant.
 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 x
-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 x
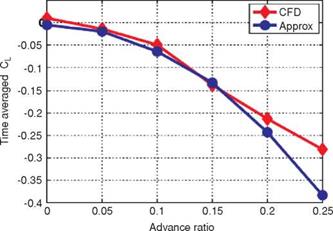
![Подпись: Figure 3.53. Time history of forces from the approximated aerodynamics model [367] and the Navier-Stokes computation [301] for a hovering flat plate at Re = 100 (delayed rotation, high AoA). When the approximate aerodynamic model assumed separated flow, including viscous effects, the agreement improved. From Gogulapati and Friedmann [367].](/img/3131/image329_3.gif)