Euler’s equations of motion for a piezotropic fluid
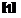 Dut 1 3p Э Cp dp
Dut 1 3p Э Cp dp
Dt p dx{ dxt Jp, p
indicate that the acceleration vector of a fluid particle,
is a gradient of a scalar quantity. Hence at can be derived from a scalar function ф(хг, x2, x3, t) so that
The function ф is then called an acceleration potential of the flow field.
Substituting Eqs. 3 into Eq. I and integrating with respect to space, we obtain
ф + f — = const (4)
Jp о p
The integration constant may be a function of time. But, if there is no change in the conditions at infinity, it is a pure constant.
і
— is a continuous function of p
Pa P
which is continuous everywhere except at a shock wave. In the thin – airfoil theory, shock waves of finite intensity do not exist; hence, in view of Eq. 4, the acceleration potential is continuous everywhere. This is in sharp contrast with the velocity potential, which does not exist in the wake. When the wake is idealized into a surface without thickness, the velocity potential is discontinuous across that surface, but the acceleration potential is continuous. This advantageous fact is very important in the application of the acceleration potential to the airfoil theory.
Further simplifications are obtained by linearization. Let us consider small disturbances in an otherwise uniform, rectilinear, steady flow. Let the deviation of each velocity component щ (і = 1, 2, 3) from the uniform, steady value be so small that щг is negligible in comparison with |и,-| itself. The corresponding changes in pressure and density of the fluid, according to the equations of motion, are also infinitesimals of the first order. Hence writing
P = Po + P’y P=Po+P’
where p0, p0 are the initial density and pressure and p, p’ are the small perturbations, then p’2 p’, p’2 p’. We have, from Eq. 4, taking ф
at p0 to be zero,
when small quantities of the second and higher orders are neglected. Hence, the acceleration potential ф is directly proportional to the pressure disturbance in the fluid. This offers a simple physical interpretation of the acceleration potential in a linearized theory.
The linearized field equations of the acceleration potential can be derived as follows.
Let us take a reference coordinate system which has no relative motion with respect to the fluid at infinity, and consider small perturbations of the velocity field so that the squares and higher powers of the velocity components or their space and time derivatives are negligible in comparison with their first power. Let p0 and p0 be the pressure and density of the undisturbed fluid, p’, p the small perturbations, and let щ be the velocity components; then the Eulerian equations of motion and the equation of continuity are linearized into
respectively. Differentiating Eq. 6 with respect to x{, and Eq. 7 with
32w.
respect to t, and eliminating the sum – we obtain
dt dxt
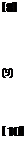 эу эу
эу эу
dxt dxi dt2
For a piezotropic fluid, if we write
dp
dp
then Eq. 8 can be written as
эу і эу
dxidxi a2 dt2
which is the fundamental wave equation in acoustics for a fluid stationary at infinity.
When small perturbations are considered,
If we neglect the second – and higher-order terms, Eq. 10 becomes
The quantity a0 is the speed of propagation of a sound wave in the undisturbed fluid. Generally a0 is written as
to signify that the derivative dpjdp is taken at the condition of constant entropy. That a0 is the velocity of propagation of a sound wave can be seen from the following example. Consider a spherical disturbance. By spherical symmetry, Eq. 11 can be transformed in spherical polar coordinates to
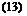
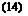 2дф
2дф
C>2 r dr a02 сП’1
A general solution of this equation is
ф = lf(r – a0t) + ^g(r + Oq0
where / and g are arbitrary functions. Clearly the first term represents a wave radiating out from the origin, and the second term one converging toward the origin, both propagating with a speed a0.
Since the acceleration potential is proportional to the perturbation pressure pr, the acceleration potential ф is governed by the same equation
дЧ 1 д2ф
Эх{ дх,; ~ V2 д?- ~ ° (15)
Differentiating Eq. 15 with respect to xjy we see that the components of acceleration = дф/дх} satisfy the same equation. Further, since p = (1 /a0V + higher-order infinitesimals, we see that p is governed by the same equation. Finally, since at = du^dt in the linearized theory, the wave equation for the components of acceleration can be integrated to show that the velocity components ut as well as the velocity potential Ф are also governed by the same equation.
If the fluid is incompressible, p = const; then a is infinity, and Eq. 15 becomes
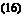 34
34
Эxt 2>x{
For an incompressible fluid in a two-dimensional flow, the governing equation
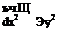 (17)
(17)
shows that there exists a function ip conjugate to ф so that w = ф + jip is an analytic function of z=x + jy. w(z) may be called a complex acceleration potential. Similar to the complex velocity function of § 12.4, the complex acceleration function
dw
— = ax-jay (18)
is the reflection of the acceleration vector in the x axis











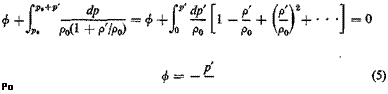
 эу эу
эу эу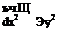 (17)
(17)
 и
и
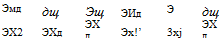 times written as curl u, has the following three components in the direction of Xj, Xg, Xg!
times written as curl u, has the following three components in the direction of Xj, Xg, Xg!