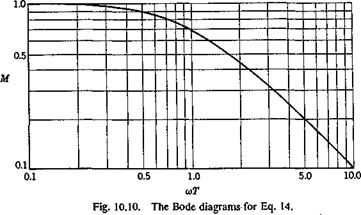
THE STRUCTURAL OPERATOR
The structural operator gives the elastic deformation of a structure under a system of external forces. If the structure is perfectly elastic, so that Hooke’s law applies, the structural operator can be concisely expressed in terms of influence functions.
A real material deviates from Hooke’s law and shows anelastic or inelastic behavior to some extent. As an important case, let us assume that the fundamental relation between stress and strain is linear, buf depends not only on the instantaneous values of stress and strain, but also on the rate of change of stress and strain.
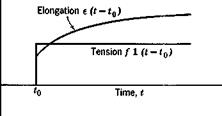
Under the linearity assumption, no permanent set remains after the removal of all stresses. To derive an expression relating the force and deformation, let us consider a simple bar which is initially free from stress. At an instant of time t0 let a tensile force /be suddenly applied and then maintained for t > ,f0. The corresponding elongation of the bar, (the indicial admittance) can be expressed in the following form:
e(t — t0) = [K + (/>(t — t0)]f for t > t0
= 0 for /</„ (1)
where A" is a constant and <f>(t — t0) is a function of time. This is represented in Fig. 11.7. The function <j>(t — t0) is generally so chosen that lim ф(/ — t0) = 0. Then К represents the limiting value of the elongation
t—> 00
є under unit tension after the transient effect is damped out. The function
|
Fig. П.7. Indicial response of a rod subject to tension. |
Фи — to) is sometimes called a “deformation function.” Note that, if Hooke’s law holds, фи — t0) = 0.
Since the stress-strain relation is linear, the principle of superposition is applicable. The response of the bar to an arbitrary loading//) can be obtained by the Duhamel integral
Ф) = KfU) + Ґ Фи – to) dto (2)
J— 00 dlQ
This result may be generalized to a three-dimensional body to show that the effect of anelasticity on the elastic deformation may be expressed by a tensor of generalized deformation function.
Anelasticity is revealed by the damping characteristics of an engineering structure (see Zener11-5). If f(t) represent a cyclicly varying force, Eq. 2 will indicate a hysteresis loop the area of which represents the dissipation of energy, and is a measure of the internal friction of the material. For a harmonic motion, a linear material has an elliptic hysteresis loop.
The internal friction may become nonlinear and depend on the life history of a material if the stress level is sufficiently high. Experiments show that the energy dissipated per cycle when a body is subjected to cyclic stresses varies with the number of cycles it has been subjected. This
phenomenon was observed in 1865 by Lord Kelvin11-2 and was called the “fatigue of elasticity.” There seems to exist a mechanism by which a metal can remember its experience, can show fatique by overworking and recovery by resting. For example, a mild steel at room temperature subjected to a cyclic stress whose extreme values lie below 80 per cent of the endurance limit shows little change of internal friction, whereas the same steel subjected to repeated stresses between this value and the endurance limit will cause an increase of internal friction as much as 25 times that of the initial value in the annealed condition (see Lazan11-3). Cyclic stresses above the endurance limit have more pronounced effects.
For built-up structures, energy dissipation may result from play in the riveted joints, from relative motion in the cracks of welding, or from the hinges of movable parts. The damping force may behave either as a viscous fluid or as dry friction, and generally depends on the amplitude of the motion. There are indications that, for built-up beams, the nonlinear component of the load-deflection curve contains mainly a second- power term, and the energy loss per cycle varies approximately as the third power of the amplitude of vibration.111,11,4
Since aeroelasticity concerns built-up structures, and yet the definitive laws of damping are unknown, more careful experiments would have to be performed in order to isolate the effect of the various parameters involved. However, for metal airplanes of conventional design, the internal friction is stnall. It may be assumed that the effect of internal friction is revealed essentially through the energy it dissipates, rather than the exact form of the stress-deformation relationship. Under this assumption we may replace the real material by a linear solid with the stipulation that the corresponding energy dissipated per cycle be the same.
In airplane structures, the elastic buckling of the sheet metal is always an important factor. As the region of buckling develops when the stress level (or the load factor) increases, the load-deflection relationship becomes a function of the load. In some oscillation problems, the amplitude of oscillation can be regarded as infinitesimal, and a correct solution can be obtained by evaluating the effective influence function at the steady-state load factor. In response problems the nonlinearity cannot always be overlooked.











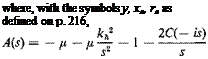
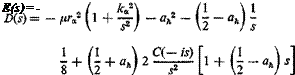
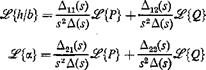 (5)
(5)
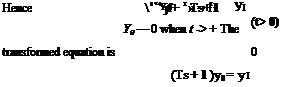
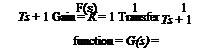

![APPLICATIONS OF LAPLACE TRANSFORMATION Подпись: [a + R1 A < R1 (s + A) < со]](/img/3130/image676_2.gif) £’{e-uF(t)}=f(s + A)
£’{e-uF(t)}=f(s + A)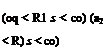
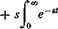 ‘ Д0
‘ Д0