Effect of Three-Dimensional Flow—Cross-Flow Instability
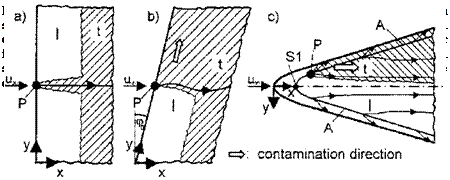
Three-dimensional boundary-layer flow is characterized by skewed boundary – layer profiles which can be decomposed into a main-flow profile and into a cross-flow profile, Fig. 7.1. With increasing cross flow, i. e., increasing three – dimensionality, the so-called cross-flow instability becomes a major instability and transition mechanism. This observation dates back to the early 1950s, when transition phenomena on swept wings became research and application topics [28]. It was found that the transition location with increasing sweep angle of the wing moves forward to the leading edge. The transition location then lies upstream of the location, which is found at zero sweep angle, and which is governed by Tollmien-Schlichting instability. Steady vortex patterns—initially visualized as striations on the wing’s surface—were observed in the boundary layer, with the vortex axes lying approximately parallel to the streamlines of the external inviscid flow, see, e. g., [52].
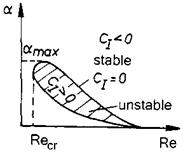
P. R. Owen and D. G. Randall proposed a criterion based on the properties of the cross-flow profile [54]. The cross-flow Reynolds number у reads with the notation used in Fig. 7.1:
у = P1’™*5* . (8.25)
Here v*max is the maximum cross-flow speed in the local cross-flow profile v*2(x3) and Sq a somewhat vaguely defined boundary-layer thickness found from that profile:
5 v*2
Sq = ~^—d, x3. (8.26)
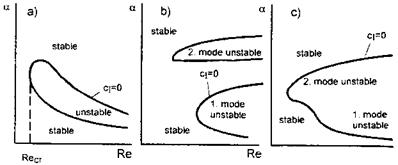
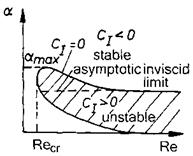
If у ^ 175, transition due to cross-flow instability happens. If the main- flow profile becomes unstable first, transition will happen, in the frame of this ansatz, due to the Tollmien-Schlichting instability like in two-dimensional flow.
The phenomenon of cross-flow instability was studied so far mainly for low speed flow, see the discussion in, e. g., [11, 14]. Experimental and theoreti – cal/numerical studies have elucidated many details of the phenomenon. Local and especially non-local stability theory has shown that the disturbance wave vector lies indeed approximately normal to the external inviscid streamlines. The disturbance flow exhibits counter-rotating vortex pairs. Their superposition with the mean flow results in the experimentally observed co-rotating vortices with twofold distance. The critical cross-flow disturbances have wave lengths approximately 2 to 4 times the boundary-layer thickness, compared to the critical Tollmien-Schlichting waves which have wave lengths approximately 5 to 10 times the boundary-layer thickness. This is the reason why non-parallel effects and surface curvature must be regarded, for which nonlocal stability methods are better suited than local methods.
The subsequent transition to turbulent flow can be due to a mixture of cross-flow and Tollmien-Schlichting instability. Typically cross-flow instability plays a role, if the local flow angle is larger than 30°. Tollmien-Schlichting instability comes into play earliest in the region of an adverse pressure gradient. However also fully cross-flow dominated transition can occur [55, 56]. For high-speed flow critical у data, however of questionable generality, have been established from dedicated experiments, see, e. g., [11, 14, 57].












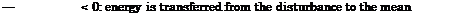 d ( _1_ du ‘
d ( _1_ du ‘