Flow Field
At zero degree angle of attack, the computed boundary layer flow on the airfoil remains attached almost to the trailing edge. The boundary layer flow is steady while the flow in the wake is oscillatory. Figure 15.31 shows a plot of the computed instantaneous vorticity field around Airfoil #2 at a Reynolds number of 2 x 105.
The leading edge of the airfoil is placed at x = 0. This is typical of all the cases investigated. The flow leaves the trailing edge of the airfoil smoothly. There is no vortex shedding at the trailing edge, regardless of previous speculation (Paterson et al., 1973). The oscillations in the wake intensify in the downstream direction until it rolls up to form discrete vortices further downstream.
Figure 15.32 shows an instantaneous streamline pattern of the wake of Airfoil #2 at a Reynolds number of 4 x 105. The wake oscillation is prominent in this figure. The wavelengths of the oscillations appear to be fairly regular. This suggests that there is flow instability in the wake.
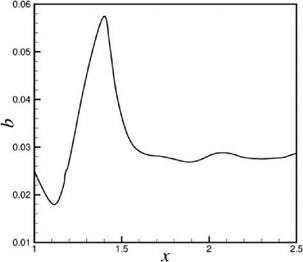
The mean velocity deficit profile in the wake resembles a Gaussian function. The half-width of the wake, b, near the airfoil trailing edge undergoes large variation in the flow direction. Figure 15.33 shows the variation of the half-width as a function of downstream distance for Airfoil #2 at a Reynolds number of 2 x 105. The width of the wake begins to shrink right downstream of the airfoil trailing edge until a
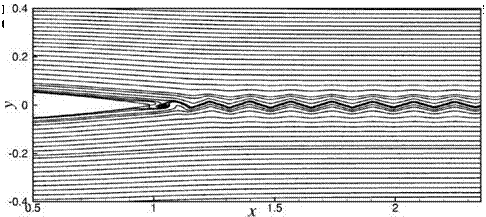 |
Figure 15.33. Spatial distribution of the half-width of the wake for Airfoil #2 at Re = 2 x 105.
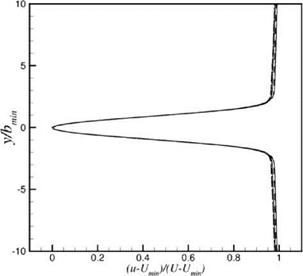
Figure 15.34. Similarity of velocity deficit profile at b = bmin in the wake of Airfoil #2. Reynolds number varies from 2 x 105 to 5 x 105 at 0.5 x 105 interval.
 minimum is reached at b = bmin. It grows rapidly further downstream, reaching a maximum before decreasing and attaining a nearly asymptotic value.
minimum is reached at b = bmin. It grows rapidly further downstream, reaching a maximum before decreasing and attaining a nearly asymptotic value.
The velocity deficit profiles of the wake exhibits self-similarity. Figure 15.34 shows a collapse of the velocity profiles at minimum half-width over a large range of Reynolds numbers. In this figure, the variable (u – Umin)/(U – Umin) is plotted against y/bmin, where Umin is the minimum velocity of the mean flow profile and b is the half-width. In Figure 15.34, data from Reynolds number of 2 x 105 to 5 x 105 at 0.5 x 105 intervals are included. There is a nearly perfect match of the set of seven profiles.
The similarity property of the wake velocity profiles suggests the possibility of the existence of a simple correlation of the minimum half-width of the wake with flow Reynolds number (Re). Figure 15.35 shows a plot of (bmin/C)Re1/2 against Re (C is the chord width) for Airfoil #2. It is seen that the measured values of this quantity from the numerical simulations are nearly independent of Reynolds number over the entire range of Reynolds number of the present study. Thus, the minimum halfwidth of the wake, bmin, of Airfoil #2 has the following form of Reynolds number dependence:
A similar analysis has been performed for Airfoil #1. Figure 15.36 shows that the quantity (bmin/C)Re1/2 again is approximately a constant. In this case, the value bmin and Reynolds number are related by,
b 1
-^Re^ «7.45. (Airfoil #1). (15.57)











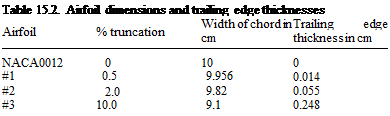
 Figure 15.30. Trailing edge profiles of the three NACA0012 airfoils under study. (a) 0.5 percent truncation, (b) 2 percent truncation, (c) 10 percent truncation.
Figure 15.30. Trailing edge profiles of the three NACA0012 airfoils under study. (a) 0.5 percent truncation, (b) 2 percent truncation, (c) 10 percent truncation.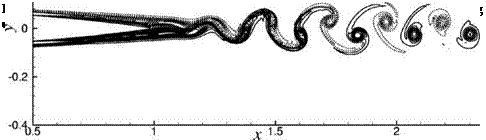
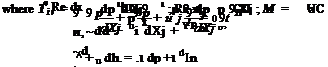
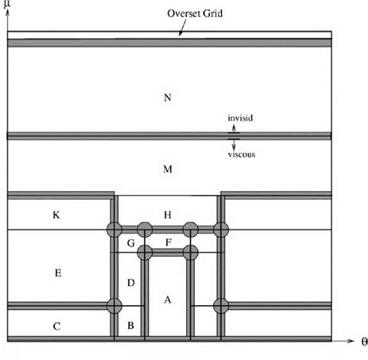
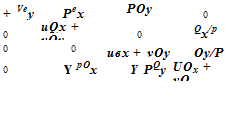
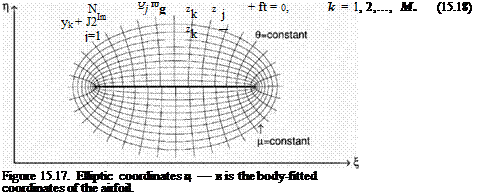
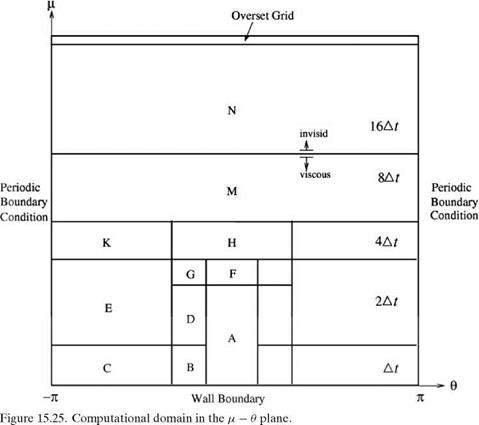
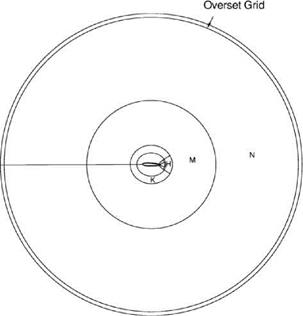 Figure 15.27. Subdomains H, K, M, and N in physical space.
Figure 15.27. Subdomains H, K, M, and N in physical space.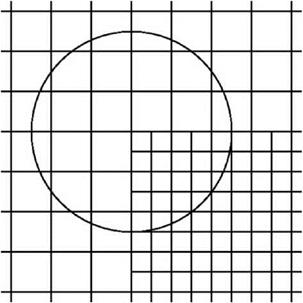 to the equations of motion. Let the coordinates of the corner point be (д0, в0), the inverse mesh Reynolds number of the extra damping term is taken to be
to the equations of motion. Let the coordinates of the corner point be (д0, в0), the inverse mesh Reynolds number of the extra damping term is taken to be
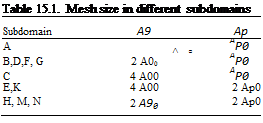
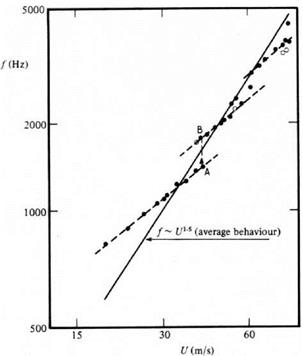 certain integral wave number requirements. The ladder structure is a consequence of a change in the quantization number of the feedback loop. At certain flow velocities, two tones were measured simultaneously. As velocity increases, the dominant tone frequency jumps to the next ladder step as indicated by A to B in Figure 15.20. This is usually referred to as staging. Further velocity increase causes the subdominant tone to vanish. By carefully analyzing their data, Paterson et al. found that the dominant tone followed a U15 power law (see Figure 15.20) where U is the free stream velocity. Based on their extensive measurements, they proposed the following formula for the dominant frequency, f:
certain integral wave number requirements. The ladder structure is a consequence of a change in the quantization number of the feedback loop. At certain flow velocities, two tones were measured simultaneously. As velocity increases, the dominant tone frequency jumps to the next ladder step as indicated by A to B in Figure 15.20. This is usually referred to as staging. Further velocity increase causes the subdominant tone to vanish. By carefully analyzing their data, Paterson et al. found that the dominant tone followed a U15 power law (see Figure 15.20) where U is the free stream velocity. Based on their extensive measurements, they proposed the following formula for the dominant frequency, f: magnitude of about five times that of the tones of Arbey and Bataille. When plotted in a frequency versus velocity diagram, the tones of Arbey and Bataille also form a ladder structure suggesting again that the tones are related to a feedback loop.
magnitude of about five times that of the tones of Arbey and Bataille. When plotted in a frequency versus velocity diagram, the tones of Arbey and Bataille also form a ladder structure suggesting again that the tones are related to a feedback loop.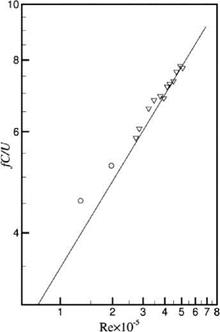 Figure 15.22. Strouhal number of dominant airfoil tone versus Reynolds number measured by Arbey and Bataille. Straight line is the Paterson formula.
Figure 15.22. Strouhal number of dominant airfoil tone versus Reynolds number measured by Arbey and Bataille. Straight line is the Paterson formula.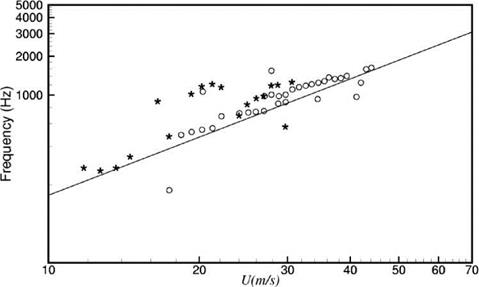
 Figure 15.16. Complex w plane. The slit is the airfoil.
Figure 15.16. Complex w plane. The slit is the airfoil.