Computational Model
The first step in performing a computational aeroacoustics (CAA) simulation is to formulate the problem. This means the development of a computational model. Usually this will include the selection of appropriate governing equations and physical boundary conditions.
In most practical CAA problems, the flow involved is turbulent (a discussion of turbulence modeling will be given in Section 15.5). Since direct numerical simulation of turbulent flow is prohibitively expensive in terms of computer resources required, some simplified method to treat the turbulence of the phenomenon is generally adopted. One may use a Reynolds Averaged Navier-Stokes (RANS) approach. The main advantage of using a RANS model is that it is easy to implement and not very expensive. The disadvantage is that it is not very accurate for time-dependent problems. Recently, the use of large eddy simulation (LES) and very large eddy simulation (VLES) has become quite popular. However, there is still a debate on how to close the LES model. One way is to use a subgrid scale model. The intent of a subgrid scale model is to model the effects of the spectrum of unresolved wave number on the resolved wave number spectrum of the computation, but it has been found that a subgrid scale model often performs only as a dissipation mechanism for the small-scale turbulence in the computation. For this reason, many investigators choose an alternative way. The alternative way is to use artificial numerical damping to remove the very small scale turbulent motion from the computation to avoid accumulation of energy in this wave number range (note: energy is cascaded up the wave number space to the highest wave number range supported by the computation). Excess energy accumulation in the smallest scales could cause a numerical simulation to blow up.
In many CAA problems, viscous effect is important only in a part of the computation domain. This may be because of a change in the dominant physics of the phenomenon in different parts of the computation domain. For example, near a wall, the viscous effect is important, while away from the wall, the compressibility effect may be most important. In such cases, the computation model will consist of the use of the Navier-Stokes equation in a part of the computation domain and the Euler equations in the remaining region.
Because a computational domain is finite, the influence of the flow and acoustic fields or sources outside may not be negligible. In such cases, the boundary conditions are forced to reproduce the outside influence as precisely as possible. In such a situation, the boundary condition is a crucial part of the computational model.











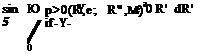
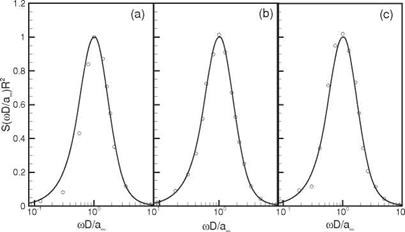
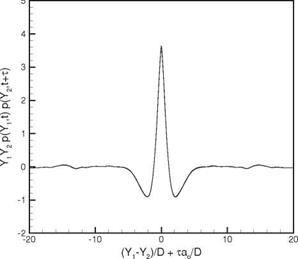 quantities of interest in the far field are the noise spectra and directivity. For this reason, only the continuation of the noise spectra from the near field to the far field at different angular direction is considered.
quantities of interest in the far field are the noise spectra and directivity. For this reason, only the continuation of the noise spectra from the near field to the far field at different angular direction is considered.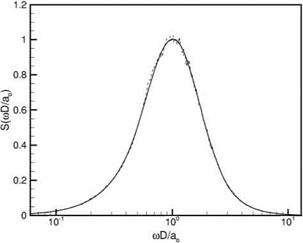 Figure 14.20. Comparison between the original (full line) and the computed spectrum (dotted line). The computed spectrum is the Fourier transform of the correlation function F (-f ) given in Figure 14.19.
Figure 14.20. Comparison between the original (full line) and the computed spectrum (dotted line). The computed spectrum is the Fourier transform of the correlation function F (-f ) given in Figure 14.19.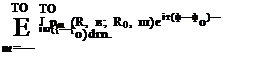
 TO TO
TO TO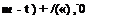
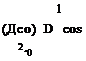
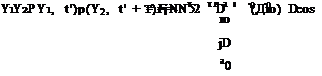
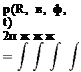 p(g)(R, в, ф; R0, ф0; m, t0)^(R0, ф0)e~imt—iQt°R0 sin 5dm dt0dR0 dф0.
p(g)(R, в, ф; R0, ф0; m, t0)^(R0, ф0)e~imt—iQt°R0 sin 5dm dt0dR0 dф0.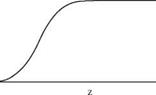 Figure 14.11. A typical profile of damping function a(z).
Figure 14.11. A typical profile of damping function a(z).
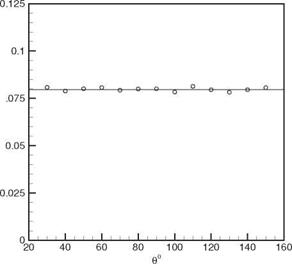 Figure 14.14. The computed directivity of a periodic monopole. The straight line is the exact solution.
Figure 14.14. The computed directivity of a periodic monopole. The straight line is the exact solution.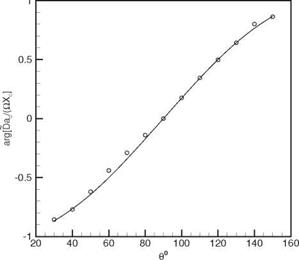 _ a D(в, Or)
_ a D(в, Or)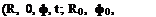
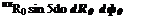 //// pig)(R, 0, ф; R0, ф0; o; Ц)Ф^0, ф0, t0)e
//// pig)(R, 0, ф; R0, ф0; o; Ц)Ф^0, ф0, t0)e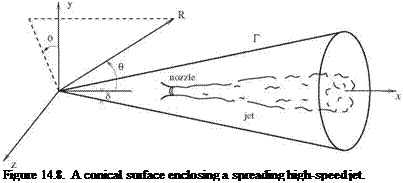
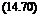 0 = 5, pm = – Jm[ —R sin 5 sin 01 ) e
0 = 5, pm = – Jm[ —R sin 5 sin 01 ) e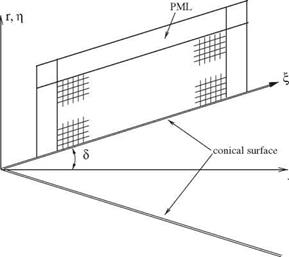
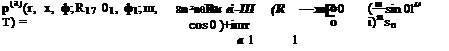
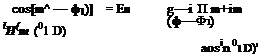
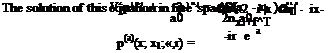
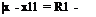 For large R1 (R1 ^ to), the distance between x1 and x is |x ■ x1|
For large R1 (R1 ^ to), the distance between x1 and x is |x ■ x1|