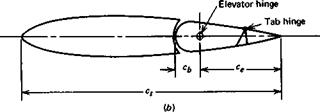
The Use of Tabs
TRIM TABS
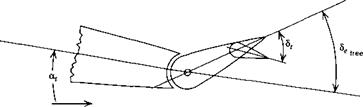
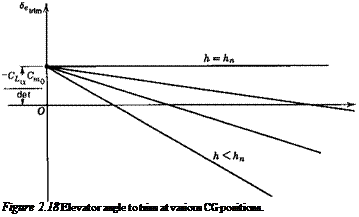
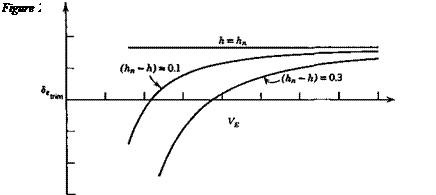
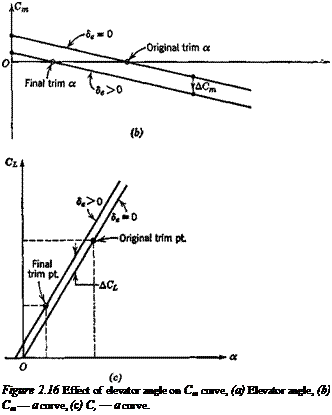
In order to fly at a given speed, or CL, it has been shown in Sec. 2.4 that a certain elevator angle Setnm is required. When this differs from the free-floating angle <5efree, a force is required to hold the elevator. When flying for long periods at a constant speed, it is very fatiguing for the pilot to maintain such a force. The trim tabs are used to relieve the pilot of this load by causing <5(,tnm and 8t, lm to coincide. The trim- tab angle required is calculated below.
When Che and Cm are both zero, the tab angle is obtained from (2.5,2) as
![]() 1
1
Jy (Cfieo CheJXtrim "h ^2^e, rim)
On substituting from (2.4,13) (which implies neglecting ЭСш/Эб(), we get
which is linear in C/irim for constant h, as shown in Fig. 2.25. The dependence on h is simple, since from (2.6,11) we find that
(CheCmSe – b2CmJ = —a’b2(h – K)
and hence
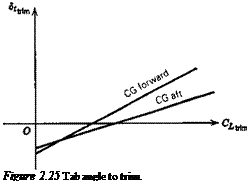 |
This result applies to both tailed and tailless aircraft, provided only that the appropriate values of the coefficients are used. It should be realized, of course, in reference to Fig. 2.25, that each different CUr. m in a real flight situation corresponds to a different set of values of M, pV2, and C7, so that in general the coefficients of (2.7,2) vary with CL, and the graphs will depart from straight lines.
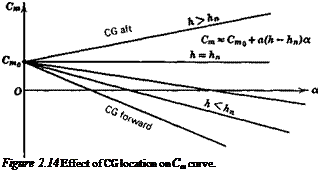
Equation (2.7,2) shows that the slope of the 5,trira vs CLtrim curve is proportional to the control-free static margin. When the coefficients are constants, we have
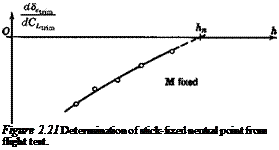
The similarity between (2.7,3) and (2.4,13c) is noteworthy, that is the trim-tab slope bears the same relation to the control-free NP as the elevator angle slope does to the control-fixed NP. It follows that flight determination of h’n from measurements of d8hr. JdCUt. m is possible subject to the same restrictions as discussed in relation to the measurement of h„ in Sec. 2.4.
OTHER USES
Tabs are used for purposes other than trimming, especially for manually actuated controls. Three of the main types are as follows:
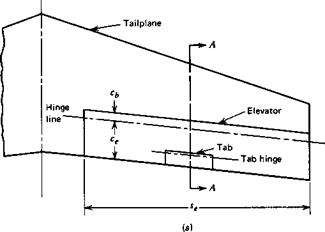
Geared Tabs. Tabs connected to the main surface by a mechanical linkage that causes the tab to deflect automatically when the main surface is deflected, but in the opposite direction. The hinge moment produced by the tab then assists the rotation of the main surface. These have the effect of reducing the b2 of the surface.
Spring Tabs. Tabs connected to the main surface by an elastic element. The design is such that the deflection of the tab depends on the dynamic pressure in a way that mitigates the effect of the speed-squared law on the control force.
Servo Tabs. An arrangement in which the pilot controls the tab directly through a mechanical linkage. It is then the tab, not the pilot, that provides the hinge moment needed to rotate the main surface.
Both spring tabs and servo tabs are effective devices for reducing control forces on large high-speed airplanes. However, both add an additional degree of freedom to the control system dynamics, and this is a potential source of trouble due to vibration or flutter.
For further details of how these tabs function, see Etkin (1972).











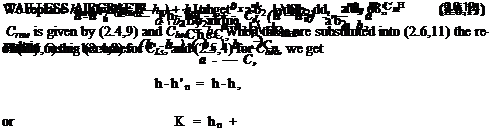
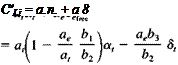 (2.6,8)
(2.6,8)
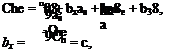
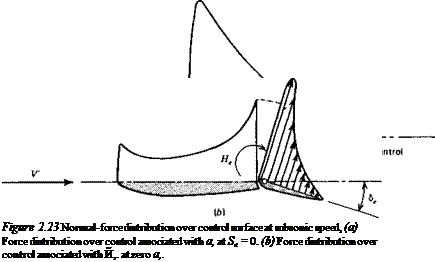
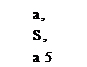
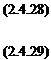
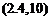 „ CJa)
„ CJa)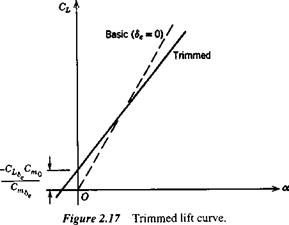
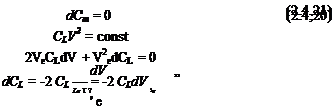

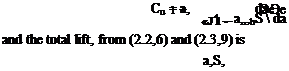
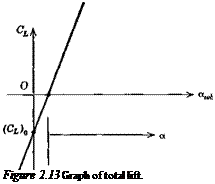
 or CL = {CL) о + aawh
or CL = {CL) о + aawh