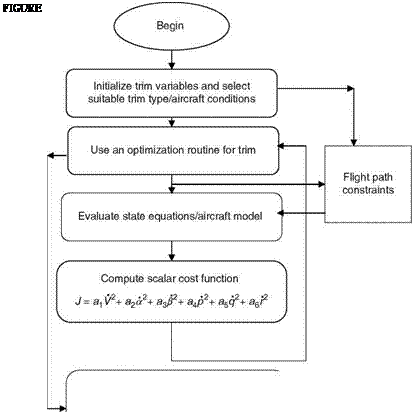
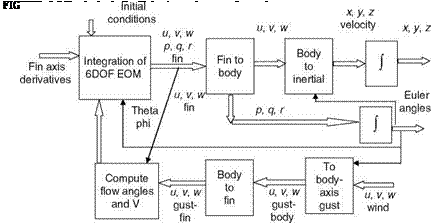
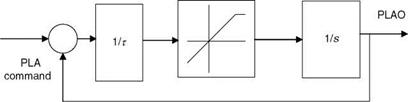
Rate of Climb and Turn Coordination Flights
In some of these the steady-state flight conditions do not apply, since with the change in the altitude the atmospheric density varies. In steady turning flight f, p, q, r will not be zero. Once the rate of climb is determined, the linearized models can be used for nonzero flight path angles. The turn is specified by ф = V, with rt as the turn radius. The angular rates can be computed from kinematic equations. A coordinated turn is such that the aircraft is banked/rolled at a required angle in order that there is no Y-axis force. This will necessitate solving the constraints for roll angle and the pitch attitude simultaneously. Following Refs. [2,15] we have the following equation for the flight path angle (assuming the wind velocity as zero):
sin g = a1 sin U — a2 cos U (6.16)
Here, a1 = cos a cos b and a2 = sin f sin b + cos f sin a cos ft. The pitch attitude is given as
a1a2 + sin g {a2 — sin2 g + a2} p
tan U =—————– 2————————– , with U = ±— (6.17)
a21 — sin2 g 2
In wings-level for b = 0, we have U = a + g.
In a coordinated turn the force Fy is assumed zero and with the steady-state condition V = 0 (the Y-axis velocity), we obtain from Equation 3.23, assuming full nonlinear EOM:
We have the conditions ф = 0 = 0, and we use the following equations
|
P |
1 |
0 |
— sin 0 |
■ф’ |
|||
|
Q |
= |
0 |
cos ф |
sin ф cos 0 |
0 |
(6.19) |
|
|
R |
0 |
— sin ф |
cos ф cos 0 |
.ф. |
to obtain the expressions for P and R as follows:
P = —ф sin 0
Q = cos ф + ф sin ф cos 0 (6.20)
R = ф cos ф cos 0
We also have the following expressions for the aircraft velocities:
|
U |
Vt cos a cos b |
||
|
V |
= |
Vt sin b |
(6.21) |
|
W |
Vt sin a cos b |
Then, substituting for R, U, P, and W in Equation 6.18 and just simplifying, we obtain the following equation:
g sin ф cos 0 = фVt cos b [cos ф cos a cos 0 + sin 0 sin a] (6.22)
Finally, we obtain the required constraint condition for the coordinated turn
![]() sin ф = – фVt cos b[cos ф cos a + tan 0 sin a]
sin ф = – фVt cos b[cos ф cos a + tan 0 sin a]
g
Next, the solution of Equations 6.17 and 6.23 together yields [2,15]:
|
|||
|
|
||
|
|||
Here, gc = ф V, the centripetal acceleration, a = 1 — gc tan a sin b, c = 1 + g’^ cos2 b, and b = sin g sec b. It must be emphasized here that Equation 6.24 would be solved by the trim routine when other required information is supplied to it. Then the value of the pitch attitude can be obtained from Equation 6.17. When the flight path angle is zero we obtain from Equation 6.24, since b is zero, the following expression:
gc cos b
cos a — gc sin a sin b
When the slide slip angle is very small, and since the flight path angle is zero, we have from the following equation:
„ , gc ФУ,
tan f = = (6.26)
cos a gc cos U