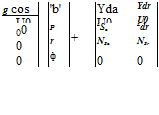Rotor Plus Body Models
As mentioned above, rotorcraft applications require at least a 6DOF model to represent the rigid body motion. Such models are generally adequate to describe helicopter dynamics associated with low frequency (such as phugoid). However, the prediction of flight dynamic behavior from such models in the high-frequency range is poor. This is due to the absence of the rotor degrees of freedom in the model, which effect the helicopter motion. Some improvements can be obtained by approximating rotor dynamics via equivalent time delay effects [7]. However, this approach cannot adequately represent the rotor influences [8]. The other alternative is to augment the 6DOF models with additional degrees of freedom that explicitly model the rotor dynamic effects, e. g., longitudinal and lateral flapping and coning. Figure 3.16 shows the submatrices that define body, rotor, and body-rotor coupling. An extended model of 8DOF can be obtained from Equation 5.38 by including longitudinal and lateral flapping in the state and observation equations [9].
xT = (u, v, w, p, q, r, f, U, ф, h, as, bs)
y (axm, aym, azm, pm, qm, rm, fm, Um, um, vm, wm, pm, qm, rm, Фт, hm, a1s, b1s)
UT = (dlon, dlab dcob dped) (5-40)
In comparison to the 6DOF rigid body model, this extended model structure can provide an in-depth insight into helicopter dynamics. However, the augmented model will have larger number of unknowns to be estimated which can lead to serious convergence problems and make identification difficult. The rotorcraft mathematical model should be such that it gives a realistic representation of the helicopter behavior and at the same time is simple and mathematically tractable. To this end, it is essential to determine the lowest-order model that would best fit the flight test data. Linear models of different order, which may include body as well as rotor degrees of freedom, can be tried out in identification. Any one of the following model structures, consistent with the frequency range of interest, can be selected for characterizing rotorcraft dynamics [10,11]:
• Body longitudinal dynamics alone—fourth-order model (3DOF)
• Body lateral dynamics alone—fourth-order model (3DOF)
• Body coupled dynamics—eighth-order model (6DOF)
• Body dynamics with first-order flapping dynamics—longitudinal and lateral tip path plane tilts—11th-order model (9DOF)
• Body dynamics with rotor flapping dynamics—15th-order model (10DOF)
• Body dynamics with rotor flapping and lead-lag dynamics—21st-order model (13DOF)
• Body dynamics with rotor flapping and lead-lag dynamics and with inflow dynamics—24th-order model (16DOF)











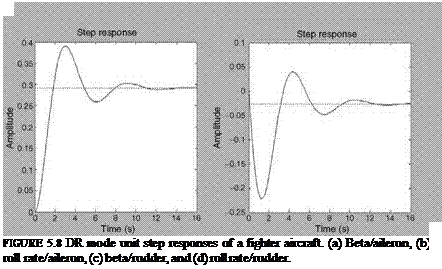
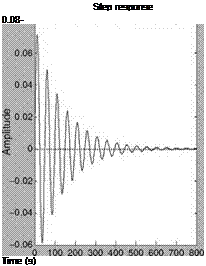
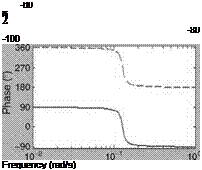
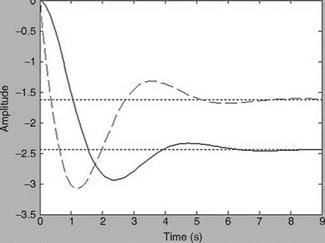
 DR Frequency and Damping Ratio
DR Frequency and Damping Ratio
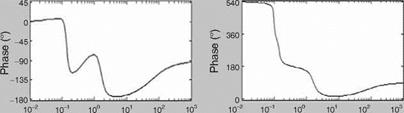
 (c) (d)
(c) (d)