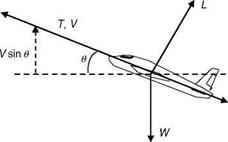
If the sum of all the resultant forces and moments acting on the aircraft is zero about its center of gravity (CG), the aircraft is in a state of equilibrium. In this condition, the aircraft is said to be flying at trim condition in a steady uniform flight. In this state, the translational and angular accelerations are normally zero.
An aircraft is said to be stable if, on encountering a disturbance during steady uniform flight, it is able to come back to its initial trim state. There are two types of stability—static and dynamic stability. An aircraft possesses positive static stability if it tends to return to its equilibrium position after disturbance. An example to illustrate this point is shown in Figure A8. The ball in position 1 is stable as it will return to its equilibrium after disturbance. The ball in position 2 is unstable as any disturbance will cause it to roll off. In position 3, the ball possesses neutral stability because, being on a flat surface, any disturbance will cause it to seek a new position. Dynamic stability, on the other hand, deals with the time history of the aircraft motion. After a disturbance, the aircraft may tend to move back because of its static
|
Position 2

|
|
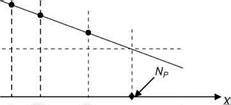
CG >NP (static instability)
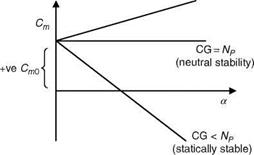
FIGURE A9 Longitudinal static stability as affected by CG location.
|
stability and settle down either monotonically or after a few oscillations. In either case, if it goes back to its equilibrium position on its own over a period of time, it is said to be dynamically stable. It should be noted that a dynamically stable aircraft must always be statically stable. On the other hand, static stability does not automatically ensure dynamic stability of the aircraft. Dynamic stability is very important for flight-control system design.
From the above explanation it is clear that if the AOA increases, the aircraft should develop a negative pitching moment so that it has the tendency to return to its equilibrium position. In other words, for an aircraft to possess static longitudinal stability, the slope of the pitching moment curve should be negative, i. e.,
m < 0 or C-a < 0 da
In addition to a negative pitching moment slope, the aircraft must also have a positive pitching moment at zero AOA to achieve trim at positive angles of attack, i. e., Cm0 should be positive (see Figure A9).
The value of Cm depends on the location of the CG. The point for which Cm = 0 defines the aft limit of the CG. At this point, the aircraft possesses neutral stability. This location of CG is called the neutral point. Estimation of neutral point from flight test data is discussed in Section A9.
Controllability is the ability to control the aircraft to maneuver and change the course of the flight path. Controllability depends on the pedal/stick force and the displacement needed to achieve the task. The faster the aircraft response to the force and displacement, the higher is the controllability.
A8 AEROSERVOELASTICITY
that can degrade the aircraft handling qualities. This interaction between the controller and the aircraft rigid body dynamics is known as aeroservoelasticity [8]. This problem can be circumvented by designing filters that eliminate the higher-frequency structural modes from the response. Normally, ground resonance and structural coupling tests are carried out on ground to determine the degree of coupling between airframe and controller dynamics. The mathematical model to study aeroservoelastic effects should account for not only the rigid body dynamics, but also the primary flexible modes of the aircraft as well as the unsteady aerodynamic effects.















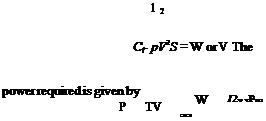
 Ma
Ma

 (A.37)
(A.37)