An atmospheric vehicle moves in the ‘‘flow field of air,’’ the atmosphere being highly dynamic. There are temperature and pressure gradients. Air pressure, temperature, and atmospheric gust and turbulence are important considerations in the study of atmospheric flight vehicles—so aptly named! In any flight mechanics study and analysis three aspects are very important: aircraft performance, stability and control, and dynamic trajectory analysis.
In the main text we have concentrated on dynamic analysis via system theoretic approach and some related highlights on stability and control. In this appendix some important useful concepts and definitions are collated.
A1 AERODYNAMIC CONCEPTS AND RELATIONSHIPS
Air Pressure
Pressure is defined as force acting on a unit area. The pressure on aircraft is usually measured by using a pitot-static system of the kind shown in Figure A1; it measures the total and static air pressure. The pressure tube is a concentric with a center tube measuring the total pressure and the outer tube measuring the static pressure. As the aircraft moves forward, the airflow comes to rest at the mouth of the pitot tube. This is known as the stagnation point and the pressure at this point is given by
Pt = Ps + 2 pV2 (A.1)
Here, Pt is the total pressure which, for flight test aircraft, is often measured at the nose boom. Ps is the static pressure upstream away from the body and V is the free stream velocity. The value of pressure 1 pV2 is termed as the dynamic pressure and is generally denoted by q. Note that dynamic pressure depends on both the density as well as the square of the velocity. Equation A.1 holds good only for low-speed flights where the compressibility effects can be ignored.
Note that both dynamic and static pressure act on the inner tube while only static pressure acts on the outer tube. The difference between the two is the dynamic pressure, which is used to determine the velocity V of the aircraft. At high speeds (M > 0.3), the pitot measurements must be corrected for compressibility effects. The corrected dynamic pressure qc can be written as [1]
Airflow oooo______
 * Чі-
* Чі-
Holes for static
pressure measurement
FIGURE A1 Pitot-static tube.
It is also worth mentioning here that static pressure is subject to errors called position errors. It is a known fact that for any given static source location, the position error varies with change in speed and altitude. The normal atmospheric pressure at sea level is 101 kN/m2. It is often expressed in terms of bars: 1 bar = 100 kN/m2. Thus, one millibar = 100 N/m2 = Pa (Pascal).
Air Density
Density is defined as the mass per unit volume:
p = mass/volume
The relation between pressure, density, and temperature is given by the equation
P = pRT (A.3)
where R is the gas constant and its value is 287 J/Kg K.
Another factor related to density, which occurs in many formulae, is the ratio of the air density p to the sea-level density p0 (its value at sea level is 1.225 kg/m3), i. e.,
s = — (A.4)
P0
The related quantity, the specific weight, is defined as weight/volume = m x g/volume. Air Temperature
The temperature of the atmosphere varies with altitude and can be represented by a linear relation
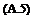 T = T1 + Ih
T = T1 + Ih
where l is the lapse rate, which indicates the rate of change in temperature with altitude. In an aircraft, a temperature probe is used to measure the total temperature of the air. Assuming adiabatic conditions (no loss of heat), the total temperature Tt in terms of ambient temperature T is given by
Altitudes
In aeronautics, we talk about several types of altitude, the primary among them being the absolute, geometric, and geo-potential altitude. Geometric altitude is the altitude/height from mean sea level. It does not vary with temperature or with the change in gravity. The absolute altitude is measured from the center of the earth. If Ha denotes the absolute altitude, HGM denotes the geometric altitude, and Re is the radius of earth, then
Ha = Hgm + Re (A.7)
If g represents the acceleration due to gravity and g0 is the gravity at sea level, then the geometric altitude can be computed from the relation [1,2]:

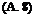

 g_ g0
g_ g0
The geo-potential altitude HGP is in fact a fictitious altitude defined based on the reference gravity at sea level (g0 = 9.8 m/s2). The relation between geometric and geo-potential altitude is given by
The difference between HGM and HGP is small for lower altitudes, but it grows as the altitude increases. Other altitudes that we frequently come across in the literature are pressure altitude, density altitude, and temperature altitude. We know that static pressure varies with altitude. A sensor called altimeter, calibrated using the standard atmosphere, measures the static pressure and relates it to altitude. The altitude indicated by the altimeter is therefore the pressure altitude. The density and the temperature altitudes, likewise, are altitudes in the standard atmosphere corresponding to the measured density and temperature. The density altitude is often used for piston engine aircraft since their power is generally proportional to air density.
Some call geometric altitude the system altitude. Some define an absolute altitude as the height above the surface of the earth at any given surface location. If the aircraft is above the mountain, then the absolute altitude is the vertical clearance between the aircraft and the surface of the mountain. Also, true altitude is defined as the height above the sea level. The pressure altitude is defined as the height from the reference where the pressure is 29.921 in. (760 mm) of mercury (Hg). Other related definitions are the Geoid height is the height of the actual surface of the Earth from the surface of the ideal spheroid of the Earth, elevation is the height from the actual surface, and geodetic height is height from the spheroid.











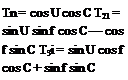
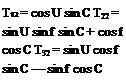
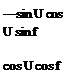
 (A.30)
(A.30)
![Подпись: 2s% 1 pV [1 + (Lu V)2] SLv 1 + 3(LvV)2 pV [1 + (LvV)2]2 SWLw 1 + 3(LwV)2 pV [1 + (LwV)2]2](/img/3131/image628.gif)
![Подпись: 2sULu 1 p [1 + (1.339 Lu V)2] 5=6 2s2 Lv 1 + 8/3(1.339 LyV)2 p [1 + (LvV)2]11/6 2s2wLw 1 + 8/3(1.339 LwV)2 p [1 + (1.339 Lw V)2]11/6](/img/3131/image631.gif)

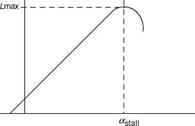
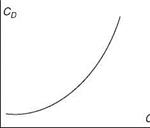
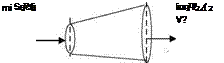
 FIGURE A3 Forces on a fluid element for developing Bernoulli’s equation.
FIGURE A3 Forces on a fluid element for developing Bernoulli’s equation.