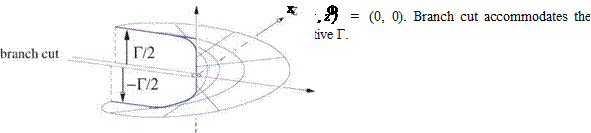
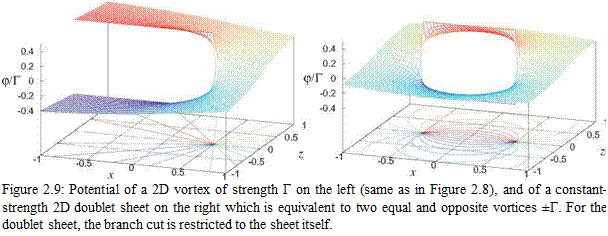
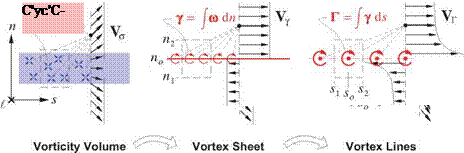
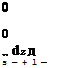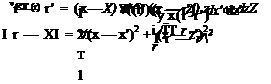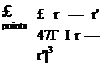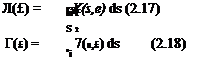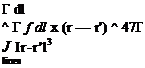Physical Requirements
The velocity field V(r) description (2.3) via the a and ш fields is purely mathematical, and in fact can be used to represent any vector field whose divergence and curl arc known. In the case of fluid flow, however, physical requirements strongly dictate and frequently simplify the magnitudes and distributions of the a and ш fields. These physically-dictated simplifications, discussed in this section, are in fact what makes this flow-field representation approach so effective in aerodynamics. Also discussed will be the flow categories where the physical constraints do not provide significant simplification.
2.2.2 Sources in incompressible flow
In the case of effectively-incompressible flow, the low-speed continuity equation (1.85) demands that a and hence А, Л, and £ are all zero within the flow-field.
V-V = 0
^ a = А = Л = £ = 0 (within flow-field) (2.57)
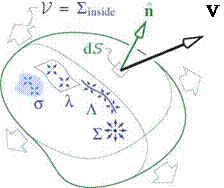
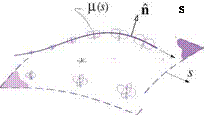
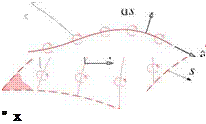
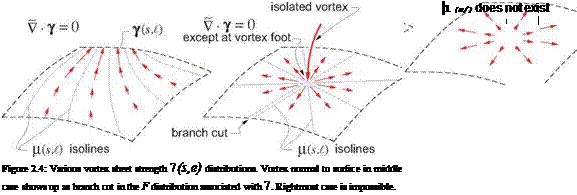
However, it is perfectly acceptable to have nonzero fictitious sources outside the physical flow-field, either within a body or on a flow boundary. Figure 2.10 shows impermissible and permissible uses of sources to represent an incompressible velocity field. The rightmost figure shows the typical use of image singularities to represent the effect of a solid wall boundary.
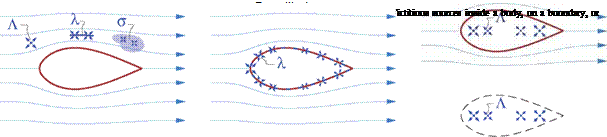 |
Permitted