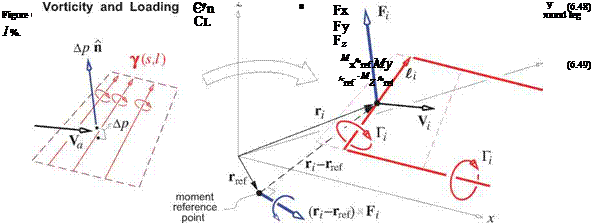
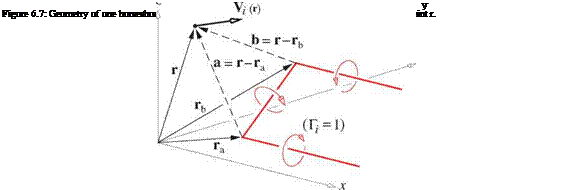
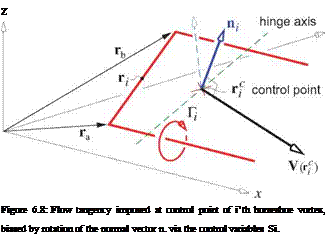
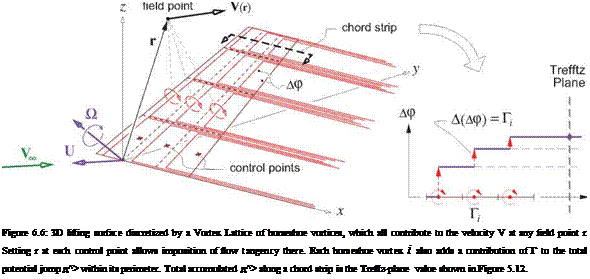
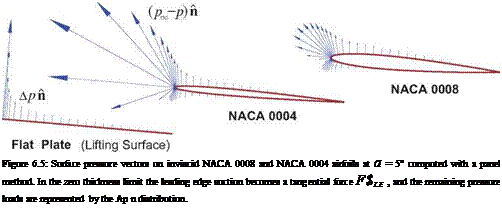
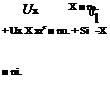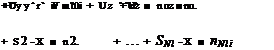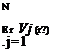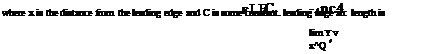Limits of slender-body theory
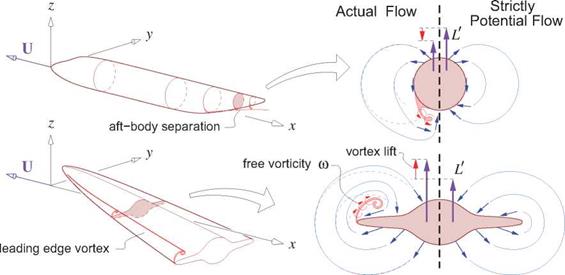
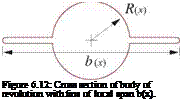
The conclusion that a rear-pointed body generates no lift assumes strictly potential flow. In reality, slender bodies will have some amount of flow separation if the rear taper is sufficiently rapid or if the local angle of attack is sufficiently large. Fuselages with large rear upsweep angles exhibit such rear separation, and slender delta wings at large angles of attack exhibit leading edge vortices. Figure 6.13 shows these flows, and compares them with their strictly-potential flow versions. Although the slender-body approximations and the 2D local far-field expansion (6.66) still remain reasonably valid with such separations, the strengths Л(х) and kz(x) will become significantly modified. In particular, the free vorticity which is antisymmetric in y will significantly modify the doublet strength kz, as can be seen from its definition (2.83). It will therefore modify the local and total lift, and also the moment. Specifically, the separation from the upswept rear body produces a downward bias in the local lift contribution, while the leading edge vortices on a delta wing significantly increase the upward lift, which is known as the vortex lift phenomenon. The effect is shown in Figure 6.14 for delta wings of two different aspect ratios.
|
Figure 6.13: Viscous separation from an upswept rear fuselage, and leading edge vortices on a delta wing at high angle of attack. The free vorticity modifies the strictly-potential flow pattern, and also modifies the 2D strengths Л(х) and kz(x), and the associated aerodynamic loads. |











 (6.71)
(6.71)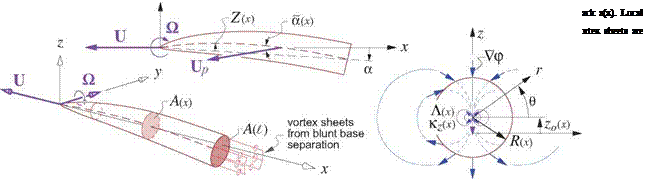
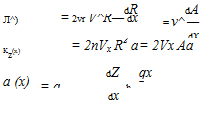 (6.72)
(6.72)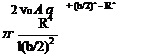
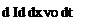 x = Vo t
x = Vo t