Axisymmetric Boundary Layers
 |
|
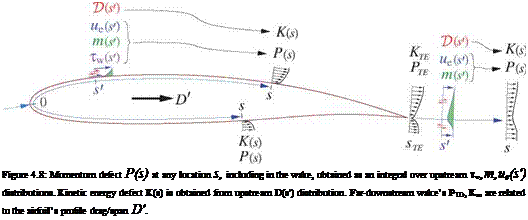
Boundary layer analysis readily applies to axisymmetric flows, such as the one shown in Figure 4.15. Extending the 2D profile drag analysis in Appendix C to the 3D case, or following the analysis in Section 5.6, we obtain the 3D profile drag in terms of the far-downstream momentum area 0W.
For the axisymmetric 3D boundary layer and wake case, the integral (4.60) is best put into axisymmetric form using the local width parameter
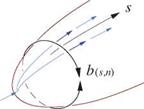
as shown in Figure 4.16. The body shape is given by the local radius function R(s), with R = 0 in the wake. The second approximate form above makes the assumption that dR/ds ^ 1, which is reasonable for slender bodies, although the exact form can be used with little complication.
|
|
||
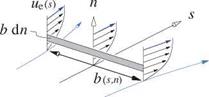
Figure 4.16: Transverse area element b dn inside boundary layer with lateral divergence, which is quantified by lateral width parameter b(s, n).
The transverse area element now becomes dS = b dn, so that at any body location the momentum area, and also the displacement and kinetic energy areas, can now be defined using the usual transverse coordinate n.
|
A*(s) 0(s) 0*(s) |
|
|||||||||||||
|
|||||||||||||
|
|||||||||||||
|
|||||||||||||
![]()
The integral equations which govern these integral areas have nearly the same form as in 2D,
|
d0 |
– c±b – – 2 |
(H + 2 – |
Me2 ) |
0 dUe |
(4.65) |
|
|
ds |
ue ds |
|||||
|
d0* |
= 2cd bavg |
/2 H** |
+ 3 |
– Me2 |
0* due |
(4.66) |
|
ds |
V H* |
Ue ds |
except for the lateral width friction factor bw = b(n=0) = 2nR, and the bavg dissipation factor which is a local dissipation-weighted average over the boundary layer thickness. The shape parameters have the same definitions as in 2D. For example, H = A*/0, etc.
A significant simplification results if we replace n in the b(s, n) definition (4.61) with a representative height in the shear layer, the rational choice being the usual 2D displacement thickness (see Figure 4.4).
b{s) ~ 2-7Г (^R + 6*/1 — (dE/ds)2j ~ 2tt(R + 5*) (4.67)
This approximate b(s) can now be taken outside of the integral area definition integrals (4.62)-(4.64), making them simply related to the usual 2D thicknesses.
![]() A* = 5*b, 0 = 9 b, 0* = 9*b
A* = 5*b, 0 = 9 b, 0* = 9*b
|
|||
|
|||
|
|
||
can also be made if we assume 5* ^ R on the body, and bavg — 5* in the wake.
|
Substitution of 0 = 6 b etc. into (4.65) and (4.66) gives essentially the 2D integral equations, (4.70) (4.71) except for the appearance of the lateral divergence terms involving db/ds. The streamwise changes in the thicknesses 6,6* resulting from these terms can be seen to be the result of a given amount of boundary layer fluid being spread over a varying perimeter b(s). However, the perimeter changes do not affect the overall amount of viscous fluid at any streamwise location, and hence cannot directly affect the overall momentum and kinetic energy areas 0, 0*. This can also be seen by the absence of explicit db/ds terms in equations (4.65), (4.66). An important consequence is that the predicted far-downstream 0TO and hence the drag will be insensitive to the details of the b(s) approximation (4.67) used here. |
|
2 H* ~H~* |
|
6* due ue ds |
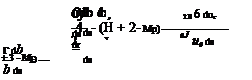 |
|
|
![]()












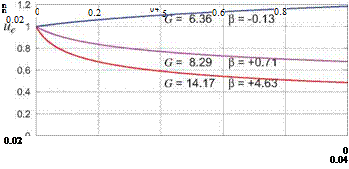

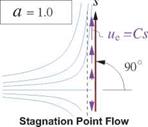
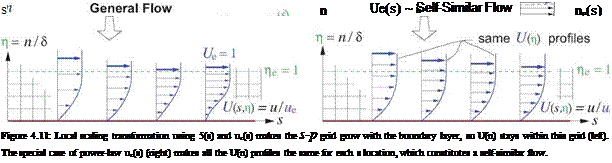
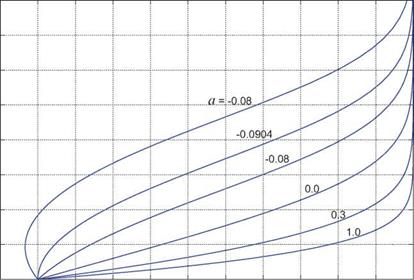
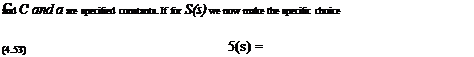
 (4.48)
(4.48)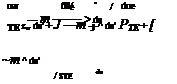
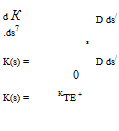
 fs due
fs due


 —— Tin)
—— Tin)
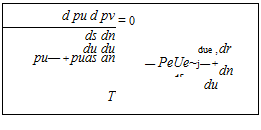 (4.21)
(4.21)