Trim Conditions Based on Elimination off Assumptions
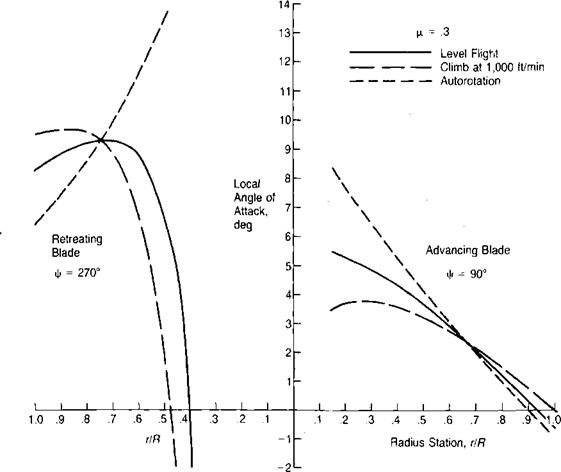
The trim conditions in level flight have been calculated while eliminating the assumptions one at a time. The results are shown in Table 3.4 for tip speed ratios of 0.30 and 0.45. (In reality, the trim conditions at the tip speed ratio of 0.45 are unobtainable for the example helicopter because of excessive blade stall, as will later be shown; but as a basis of comparing the effects of the various assumptions, it is an illustrative case.) It may be seen from Table 3.4 that the elimination of the assumption that there are no root or tip losses makes relatively little difference in the trim conditions at the low speed but makes a significant difference at high speeds. This is due to the large reduction in the H-force and the consequent reduction in the nose-down attitude of the rotor. The reduction in H-force can be traced to the variation in the calculated induced drag in the tip annulus as a function of azimuth position. Because of the higher dynamic pressure on the advancing tip, the induced drag is higher on the advancing side, where it contributes to positive H-force, than it is on the retreating side, where it contributes to negative H-force. Thus the elimination of the induced drag in this annulus by considering it lost due to tip effects results in a net decrease of the calculated H-force.
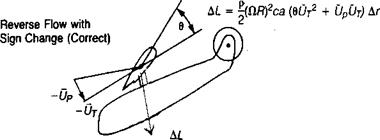
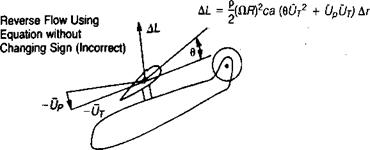
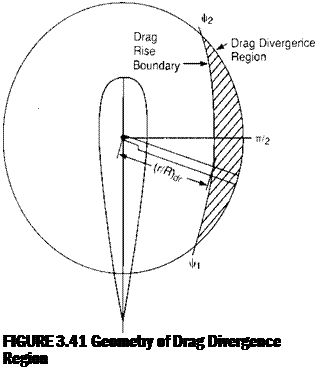
The effect of treating the reverse flow region correctly is shown in Table 3.4. At a tip speed ratio of 0.3, the main rotor power is increased approximately 6%, but at a tip speed ratio of 0.45 it is decreased about 10% compared to the corresponding calculation with the reverse-flow region treated incorrectly. At the lower speed, the increase in rotor thrust in the normal-flow region requires higher power. At the higher speed, the reduction in the H-force due to the reversal of the lift vectors in the reverse-flow region, as shown in Figure 3.50, has resulted in a large reduction in the rotor angle and thus has put both the rotor and the fuselage into a more favorable condition with respect to overall power.
The use of a three-term drag polar in place of an average value has an effect similar to those caused by eliminating the first two assumptions—relatively little effect at the low speed, but a dramatic decrease in rotor power at the high speed. Again, this reduction can be traced to the decrease in H-force and the more favorable rotor and fuselage attitude that results. Paradoxically, this is due to the increase in drag on the retreating side, where the contribution to H-force is negative.
The logical next step would be to present all the closed-form rotor equations with the assumptions eliminated. This step, however, has been bypassed in favor of developing the charts at the end of this chapter, which are based on a digital computer program. This program, in using rigorous equations for the
|
TABLE 3.4 Effect of Eliminating Assumptions on Trim Conditions for Example Helicopter
|
forces at the blade elements, automatically eliminates the assumptions while also including the effects of compressibility and unsteady aerodynamics, which are difficult to include in any closed-form analysis.
![]()
Numerical integration methods use the same basic equations for the forces on a blade element as do closed integration methods, but because of the nature of the computer, which doesn’t mind boring, repetitive computations, fewer assumptions need be used. A primary advantage of these methods is their ability to use two – dimensional airfoil data as a function of angle of attack and Mach number throughout the complete ranges of these two parameters as they exist on the rotor. In addition, the methods can be made—with ever-increasing complexity—to handle unsteady aerodynamics, yawed flow characteristics, complicated induced velocity patterns, blade flexibility, and lifting surface (rather than lifting line) aerodynamics.
A requirement of any program is that it have the capability to find the trim condition in which the blade inertial, centrifugal, and aerodynamic forces and moments are all in equilibrium, as they must be for a rotor in steady flight. There are two starting approaches for a hinged rotor. In the most common, the computer calculates the flapping by following one blade around the azimuth while continually evaluating its flapping acceleration, velocity, and displacement. For a reasonable set of shaft angles and control settings, the calculations will converge on a condition where the flapping repeats itself from one revolution to another. The other blades in the rotor are assumed to fly in the same path. This method is sometimes referred to as a flapdoodle. If it is required to trim the first harmonic flapping to zero with respect to the shaft, the computer changes cyclic pitch in a logical way to do this. Once this condition is achieved, the flapping hinges could be locked. In this situation, the longitudinal and lateral hub moments would be zero, since the tip path plane is perpendicular to the shaft.
The second method—and the one that will be used here—obtains the same results by starting first with locked hinges. On this rotor, changes in cyclic pitch result in aerodynamic pitching and rolling moments. The computer searches for the cyclic pitch that reduces these moments to zero, thus giving the same results as those obtained with the more common method. Because of the equivalence of flapping and feathering demonstrated in the previous analyses, the trim values of cyclic pitch can be reidentified as (Вг + ax ) and {Ax — bj) and thus applicable to flapping rotors in which the tip path plane is not necessarily perpendicular to the shaft.
The second method gives the same results as the first except for the loss of flapping harmonics above the first. Studies have shown that these have little effect on rotor performance, so their loss is not serious for our purposes. Comparison of the two methods indicates that the second is more economical in computer time and will often converge to a trim solution at extreme conditions, where the flapdoodle procedure will diverge because of second-order effects.
The method outlined in the following paragraphs is suitable for a mediumsized computer and is based on the following limitations and assumptions:
• Obtaining performance and trim conditions is the primary objective.
• Two-dimensional airfoil lift and drag characteristics are available.
• The blades do not bend or twist elastically.
• The induced velocity distribution is given by the equation:
( r.
VL = v I 1 + ——————— Sin |/ I











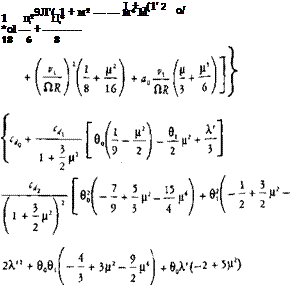
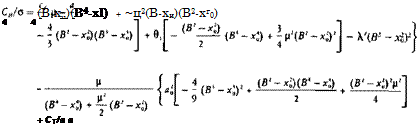






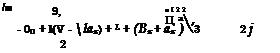

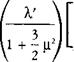
 9 2 ) 3 CLR 8 CLRj
9 2 ) 3 CLR 8 CLRj