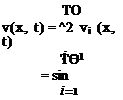For a beam undergoing pure torsion, one boundary condition is required at each end. Mathematically, boundary conditions may affect 0 as well as its partial derivatives, such as д0/dx and d20/dt2, at the ends of the beam. In the context of the separation of variables, these conditions lead to corresponding conditions on X and/or X’ at the ends. These relationships are necessary and sufficient for determination of the constants A and B to within a multiplicative constant.
The nature of the boundary condition at an end stems from how that end is restrained. When an end cross section is unrestrained, the tractions on it are identically zero. Conversely, the most stringent condition is a perfect clamp, which allows no rotation of an end cross section. Although this is a common idealization, it is practically impossible to achieve in practice.
Cases that only partially restrain an end cross section involve elastic and/or inertial reactions. For example, an aircraft wing attached to a flexible support, such as a fuselage, is not a perfect clamped condition; the root of the wing experiences some rotation because of inherent flexibility at the point of attachment. A boundary condition that is idealized in terms of a rotational spring may be used to create a more realistic model for the support flexibility. Appropriate values for support flexibility can be estimated from static tests. Boundary conditions involving inertial reactions may stem from attached rigid bodies to model the effects of fuel tanks, engines, armaments, and so on.
Figure 3.10. Clamped end of a beam
 In this section, we consider two boundary conditions of the “primitive” type and two examples of derived boundary conditions that can be imposed at the ends of the beam to determine the constants A and B.
In this section, we consider two boundary conditions of the “primitive” type and two examples of derived boundary conditions that can be imposed at the ends of the beam to determine the constants A and B.
Clamped End. In this first primitive case (Fig. 3.10), the x = £ end of the beam is assumed to be clamped or rigidly attached to an immovable support. As a consequence, there is no rotation due to elastic twist at this end of the beam, and the boundary condition is
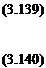 в(£, t) = 0 = X(£)Y(t) which is identically satisfied when
в(£, t) = 0 = X(£)Y(t) which is identically satisfied when
X(£) = 0
Free End. For the second primitive case, we consider the x = £ end cross section of the beam to be free of stress (Fig. 3.11). Therefore, the twisting moment resultant on the end cross section must be zero
T(£, t) = GJ(£) — (£, t) = 0 (3.141)
d x
Because GJ(£) > 0, this specializes to
дв
(£, t) = X'(£)Y(t) = 0 (3.142)
д X
Thus, the specific condition to be satisfied is
X'(£) = 0 (3.143)
Other Forms of End Restraint. In any cross section of a beam undergoing deformation, there is a set of tractions on the plane of a typical cross section; a traction is a projection of the stress (three-dimensional) onto a surface (two-dimensional). From tractions at a given cross section, we can define the resultant force and moment at that station of the beam. When the end of a beam is connected to a rigid body, the
body exerts forces and moments on the beam that are balanced by the distributed traction on the end cross section. That is, the force and moment resultants on the end cross section are reacted by equal and opposite forces and moments on the rigid body. These facts, along with application of suitable laws of motion for the attached body, allow us to determine the boundary conditions.
In the case of torsion, for any cross section, the resultant moment about x of tractions caused by transverse shearing stress has the sense of a twisting moment, T, given by
__ dQ
T = GJ — (3.144)
dx v ’
With x directed to the right and the outward-directed normal along the positive x direction at the end of the beam where x = l, a positive twisting moment is directed along x in the right-handed sense. To avoid coupling with transverse motion, we stipulate that the mass center C of the attached rigid body lies on the x axis (i. e., the elastic axis of the beam). The body has a mass moment of inertia IC about C so that it contributes a concentrated rotational inertia effect on the beam. The free-body diagram for the problem is then as shown in Fig. 3.12. By Newton’s third law, the beam’s twisting moment produces an equal and opposite torque on the rigid body.
Recall that Euler’s second law for a rigid body is stated precisely in Section 2.1.2. The only forces acting on the rigid body here3 are the contact forces from the beam. So, the x component of the left-hand side of Euler’s law is the sum of all moments acting on the body; that is
(EM)x = – T(l, t) (3.145)
where the sign in front of T is negative because of the free-body diagram and the sign convention, which has moments acting on the body as positive in the same direction as the rotation of the body—along x in the right-handed sense. The x component of the right-hand side is the inertial time derivative of the inertial angular momentum about C, here simply the moment of inertia times the angular acceleration:
where the left superscript on the left-hand side reflects the fact that the time derivative is taken in the inertial frame F, defined in Section 2.1.2. Euler’s law for this rigid
 Recall that we normally ignore gravity for free-vibration problems.
Recall that we normally ignore gravity for free-vibration problems.
This equation then expresses the boundary condition of a beam undergoing uncoupled torsional vibration with a rigid body attached at x = l.
When the body is attached to the x = 0 end, there is a subtle but important difference. With x directed to the right and the outward-directed normal along the negative x direction at the x = 0 end of the beam, a positive twisting moment is directed along – x in the right-handed sense. The free-body diagram for the problem is then as shown in Fig. 3.13. By Newton’s third law, the twisting moment produces an equal and opposite torque on the rigid body, which is in the direction of a positive rotation for the body. Therefore, Euler’s law (and the resulting boundary condition) is written as
d 2В
T(0, t) = Ic(0, t) (3.149)
or
__ dQ d2$
GJ — (0, t) = Ic^(0, t) (3.150)
Thus, this equation expresses the boundary condition of a beam undergoing uncoupled torsional vibration with a rigid body attached at x = 0.
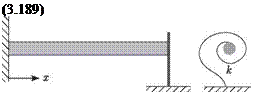
The following example illustrates a convenient way to think about the contribution of a spring to the boundary of a beam undergoing only torsional rotation. Consider a beam with an attached rigid body at its x = l end, such that the rigid body is, in turn, restrained by a light torsional spring attached to the ground. The rotational sign convention does not change; В is always positive in the x direction (i. e., to the right in the sense of the right-hand rule). The rigid body, because it is attached to the end of the beam, rotates by В (l, t). Thus, the rotational spring reacts against that rotation, and the moment applied by the spring to the body is opposite to the direction of the rotation (Fig. 3.14). The boundary condition for the beam results from applying Euler’s second law to the rigid body, so that
d 2q
-кВ(l, t) – T(l, t) = Ic —7(1, t) (3.151)
d t2
If the body-spring mechanism is instead on the x = 0 end of the beam, then the moment exerted by the spring is still in the same direction. However, what constitutes a positive twisting moment on the beam has the opposite sense, and the boundary condition changes to
d 2в
-кв(0, t) + T(0, t) = Ic(0’t) (3.152)
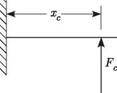
Clearly, if the body is absent, one may set Ic = 0. Then, the problem reduces to the elastically restrained boundary condition, as shown in Fig. 3.15. The twisting moment at the beam end must be equal and opposite to the spring reaction for any finite rotation due to twist at the x = l end, so that
__ дв
-T(l, t) = – GJ—(l, t) = кв(l, t) (3.153)
д X
At the x = 0 end, however
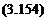
___ дв
T(0, t) = GJ—(0, t) = кв (0, t)
д X
To be useful for separation of variables, we must determine the corresponding boundary condition on X. Thus, we write в(x, t) as X(x)Y(t) as before, yielding
Readers should verify that the same type of boundary condition at the other end would yield
GJX’ (0) = kX(0) (3.157)
where the sign change comes about by virtue of the switch in the direction noted previously for a positive twisting moment.
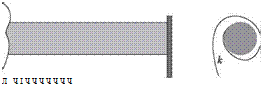 Figure 3.15. Elastically restrained end of a beam
Figure 3.15. Elastically restrained end of a beam
Figure 3.16. Inertially restrained end of a beam
 Conversely, if the spring is absent, we may set к = 0, and the problem reduces to the inertially restrained case with only a rigid body attached to the x = l end (Fig. 3.16). The twisting moment at the beam end must be equal and opposite to the inertial reaction of the concentrated inertia for any finite angular acceleration of the end. Therefore
Conversely, if the spring is absent, we may set к = 0, and the problem reduces to the inertially restrained case with only a rigid body attached to the x = l end (Fig. 3.16). The twisting moment at the beam end must be equal and opposite to the inertial reaction of the concentrated inertia for any finite angular acceleration of the end. Therefore
__ dQ d2$
-GJ—(l, t) = Ic^(£, t) (3.158)
Expressing this condition in terms of X(x), Y(t), and their derivatives, we find that
-GJX'(l)Y(t) = IcX(t)Y(t) (3.159)
From separation of variables, it was determined from the second of Eqs. (3.137) that for free vibration (i. e., no external forces), we may regard Y(t) as describing simple harmonic motion; that is
Substitution into the preceding condition then yields
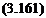 __ GJ
__ GJ
GlX'(l)Y(t) = a2 IcX(l)Y(t)
P Ip
which requires that
p IpX'(l) = a2 IcX(I) (3.162)
As before, readers should verify that the same type of boundary condition at the other end would yield
p IpX'(0) = – a2 IcX(0) (3.163)
It is appropriate to note that the use of Eq. (3.160) allows us to express Eq. (3.158) as
__ dQ
GJ—(l, t) = Ш2IcQ(l, t) (3.164)
д X
with the caveat that this condition holds true only for simple harmonic motion.
![]()
![]()
![]()
![]()
![]()
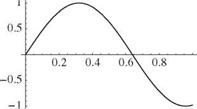
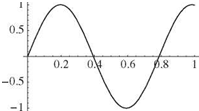
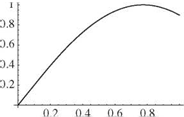











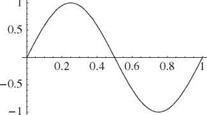
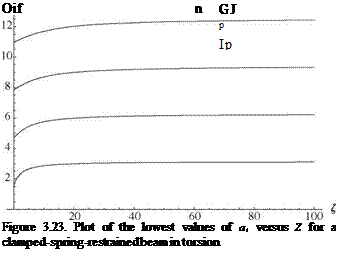
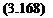 It is apparent that the boundary conditions lead to the following X(0) = 0 requires B = 0 X'(l) = 0 requires Aa cos(al) = 0
It is apparent that the boundary conditions lead to the following X(0) = 0 requires B = 0 X'(l) = 0 requires Aa cos(al) = 0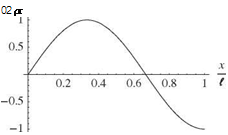
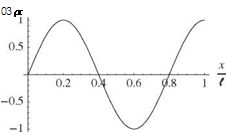

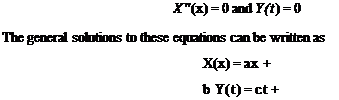
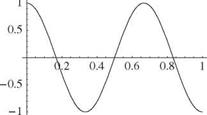

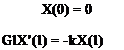
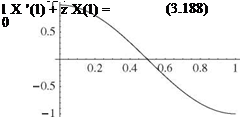
 Z tan(al) + al = 0
Z tan(al) + al = 0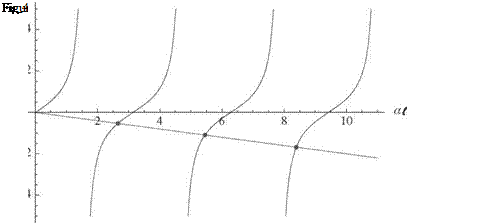
 In this section, we consider two boundary conditions of the “primitive” type and two examples of derived boundary conditions that can be imposed at the ends of the beam to determine the constants A and B.
In this section, we consider two boundary conditions of the “primitive” type and two examples of derived boundary conditions that can be imposed at the ends of the beam to determine the constants A and B.
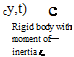



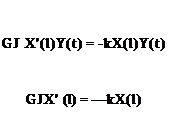
 Figure 3.15. Elastically restrained end of a beam
Figure 3.15. Elastically restrained end of a beam Conversely, if the spring is absent, we may set к = 0, and the problem reduces to the inertially restrained case with only a rigid body attached to the x = l end (Fig. 3.16). The twisting moment at the beam end must be equal and opposite to the inertial reaction of the concentrated inertia for any finite angular acceleration of the end. Therefore
Conversely, if the spring is absent, we may set к = 0, and the problem reduces to the inertially restrained case with only a rigid body attached to the x = l end (Fig. 3.16). The twisting moment at the beam end must be equal and opposite to the inertial reaction of the concentrated inertia for any finite angular acceleration of the end. Therefore
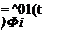
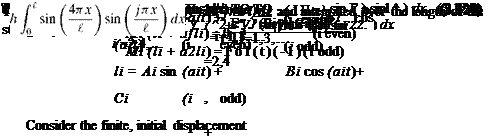
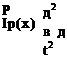
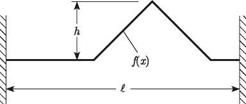
 generalized coordinates and mode shapes as
generalized coordinates and mode shapes as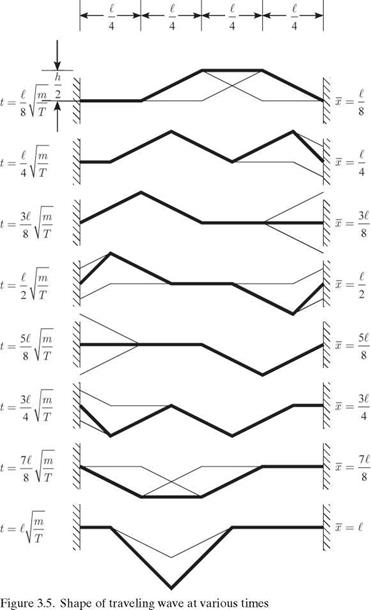

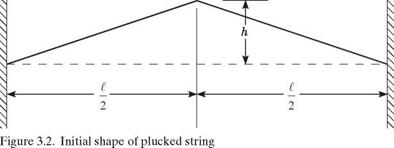
 General Evaluation of f (x ± Vt). These two properties can be applied simultaneously for the evaluation of f (x + Vt) and f (x – Vt) for any value of their argument—say, x ± Vt. When this argument lies within the range
General Evaluation of f (x ± Vt). These two properties can be applied simultaneously for the evaluation of f (x + Vt) and f (x – Vt) for any value of their argument—say, x ± Vt. When this argument lies within the range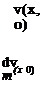
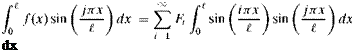
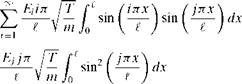
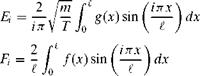 (3.48)
(3.48)![Using Orthogonality Подпись: [Ei sin(«;t) + Fi cos(«;t)]](/img/3130/image158_2.gif)
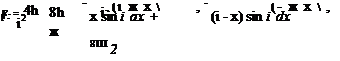
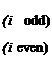
![Orthogonality of Mode Shapes Подпись: aa u = фі X 43 II s 43 v = Ф] dv = ф'-йх u = ф j X 43^ 3=7 II s 43 v = ф'і dv = ф"йх](/img/3130/image143_2.gif)