To disturb equilibrium, changing the speed or direction of flight in any way, requires a force variation to bring about an acceleration in the appropriate sense. The second law of
Fig. 1.1 Static and dynamic equilibrium
a Body standing on ground; no relative motion: static equilibrium.
b Vehicle moving at steady rate; no acceleration or deceleration: dynamic equilibrium.
d Model climbing, diving or gliding at steady rate and constant speed: dynamic equilibrium.
|
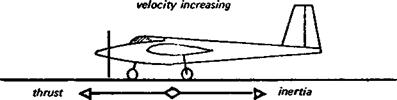
Fig. 1.2 Inertia
a Model accelerating from standstill
———— <3—————————– Cj—–
|
|
|
Model in accelerating dive
|
|
|
|
|
Model in turn acceleration inwards ^
|
|
|
|
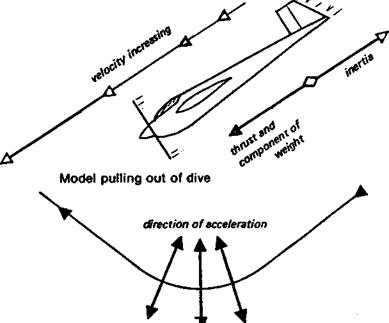
motion states that the strength of force required for any given acceleration depends on the mass of the model. Mass is not the same as weight, although in ordinary language, and on the kitchen scales, the two are often equated. Weight is force exerted by a mass. If a model were taken by rocket to Mars for trials in the atmosphere there, it would, during most of the trip, exert no weight, and on arrival would weigh less than on Earth, because of the lower gravity. The mass would be unchanged throughout, because the quantity of material, balsawood, metal, plastic, glue etc., in the model would be the same. An object of large mass requires greater forces to disturb its equilibrium to any given extent than a small mass. This is sometimes advantageous, as when a model is affected by air gusts. A model of small mass might be overturned by a force that would cause only a minor change of direction with a large mass. But the larger mass also requires a larger force to accelerate it to flying speed from standstill, more force to change level flight to climb, more force to initiate and maintain a turn, and more force to bring the model to a standstill again after flight. Whenever there is a disturbance of equilibrium, i. e. an acceleration or deceleration, or a change of direction, this quality of mass, termed inertia, opposes the change. In a turn, inertia tends to make the model revert to straight flight Turning flight is a form of lateral acceleration. Pulling out of a dive involves a change of direction in the vertical plane, mass resists and tends to make the dive continue (Fig. 1.2).
1.1 LAWS OF MOTION
All aerodynamic theory depends on the laws of motion. These, originally worked out by Isaac Newton, remain entirely valid in engineering providing the matters under discussion are confined to velocities substantially less than the speed of light, and to objects and fluids of ordinary sizes and densities. Quantum mechanics and the theory of relativity, although fundamentally preferable to the Newtonian laws in advanced physics and astronomy, are not necessary for the understanding of model aircraft aerodynamics.
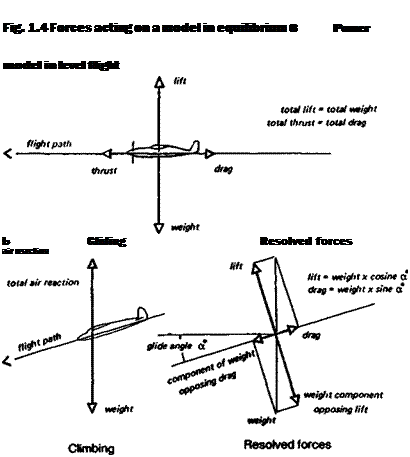
1.2 EQUILIBRIUM
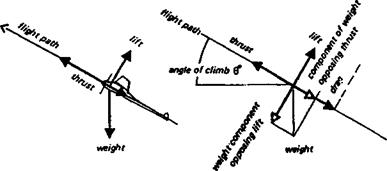
If a body is in equilibrium, it tends to remain so. All the forces acting cm an object in equilibrium are in balance, there is no tendency for it to change its state or accelerate in any direction, or decelerate. This is familiar with respect to things standing on the ground like items of furniture, or a model aeroplane lying on a shelf or workbench, not moving. Such bodies stay put unless something disturbs them, i. e. accelerates them in some way. Moving objects may also be in equilibrium. A model flying straight and level in calm air, neither speeding up nor slowing down, nor turning, is in a balanced state, and will tend to continue moving steadily. The same is true if die model is climbing at a constant speed in straight flight It is in equilibrium even though gaining height, and will continue steadily along its inclined path unless some change of the forces acting on it occurs. Even if the climb is truly vertical, so long as the speed remains steady and there are no changes of direction, equilibrium prevails. In a steady speed dive the same applies (Figure 1.1). Equilibrium, then, is a very common state of affairs. It is a condition of steady motion or rest, in contrast to states of unsteady motion involving acceleration and negative acceleration or deceleration.
The purpose of this book is to present in a practically useful form some standard aerodynamic theory as it applies to model aeroplanes, helicopters and gliders.
‘ Anyone whose interest in aeromodelling is more than casual will benefit from under – 5 standing the behaviour of his models better. He is less likely to make serious mistakes in j, trimming or control, will build better, and may be able to improve the design of models. lApart from these considerations, aerodynamics is an interesting study in its own right and pods a further fascination to the sport.
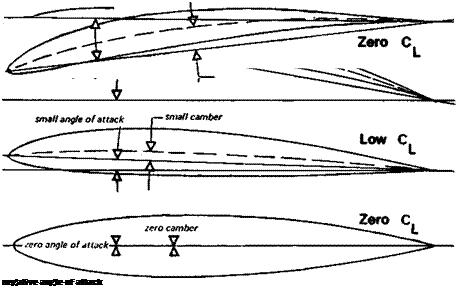
I Successful models may be designed and flown by rule of thumb. A sort of evolution – Jjtfy survival of the fittest has produced a great many extremely efficient aircraft and it is claimed that this book will bring about any revolution. It is, however, likely that some iw ideas for future development will be extracted by those who read with an open mind. ie of the material contained will be familiar to experienced modellers, but in other they will find their old notions under criticism. This is particularly likely in sions of the basic description and selection of aerofoil sections. Model fliers and іу books and articles written for them frequently adopt a very misleading aerofoil enclature: undercambered, flat bottomed, semi-symmetrical and symmetrical. These s can lead the beginner into serious trouble. At least the camber of the centre line of profile should be known and taken together with the profile thickness.
I The basic layout and trim of nearly all ‘free flight’ models also seems to be dominated fashion to the exclusion of elementary principles. This is not to say that these models not fly well; clearly they do. But trimming them for consistent performance and safety lade unnecessarily difficult when the centre of gravity is in the wrong position relative the mainplane, as it almost invariably is. No gain in performance results, indeed, there ie small performance penalty for slow-flying models if the centre of gravity is located , on current contest-winning models, it usually is. The fact that such models do win ause they are flown very skilfully despite their inherent faults. Arguments in favour this kind of trim, sometimes loaded with mathematical equations, prove on ation to be mistaken.
Other common misunderstandings arise through the confusion between trimming and ibility. This is examined in some detail in Chapter 12.
It is assumed throughout that the reader is a practising model flier and knows at least essentials of how model aircraft are constructed, trimmed and flown. The lematics have been kept to a bare minimum. Where numerical examples have been ight important or interesting enough to merit inclusion, they have been placed in an ndix and may be ignored by those who do not wish to become involved in figuring. It
is rarely necessary or worthwhile in aeromodelling to carry out elaborate calculations; when a little arithmetic is essential it is usually confined to the four basic rules. The underlying principles are emphasised throughout Where a reader is prepared to do a little more work, many of the problems arising can be solved to a sufficient degree of precision by the use of simple graphical methods or at most with an ordinary pocket calculator. It helps to have a few additional functions such as square roots and trigonometrical ratios (Cosines, Sines, Tangents etc.), but these are not essential.
On the commercial market now there arevarious kinds of copiputer software packages with model aircraft applications. These range from glider performance programs to flight simulators and elementary aerofoil section design. (These last should be distinguished from the highly sophisticated programs used for aerofoil design by professional aerodynamicists such as Eppler, Somers, Williams etc. in university and other research institutions.) Modellers using any such packages should remember that they are all based on fundamental assumptions which may be wrong. If garbage goes into the computer, it emerges in the output Even with a sophisticated machine it is most necessary to comprehend the underlying theory if the computer is to produce meaningful results. This book should provide the necessary background enabling the model flier to discriminate between sense and nonsense.
The theories discussed are in general use by aerodynamicists but are not to be regarded і as final truths. There is always room, and in some cases great need, for new discoveries. ; On the other hand, model aerodynamics, like any other branch of engineering science, must be firmly based on fundamental natural principles as these have been found by test and experiment. Some of the most basic principles are examined in the first chapter. Readers already familiar with the laws of motion may wish to skip this early section, though it is important that these passages be understood before the later ones are tackled.
Problems associated with flight and airflow speeds approaching the speed of sound are not considered in this book.
1
In the third edition the main text remains but the opportunity has been taken to include brief discussion of the important wind tunnel research undertaken at Princeton University by Selig, Donovan and Fraser during the years 1986—89. Also an explanation of the effects of wind on model flying has been included since so much misunderstanding surrounds this topic. There is an expanded section on tip winglets and crescent wing planforms. The discussion of the centre of lateral area theory has been expanded and the practice of trimming sailplanes using the so-called dive test is examined in relation to the dangerous phenomenon of ‘tucking under’. The section on air brakes has been expanded to include the ‘crow’ or ‘butterfly’ mix system. A few other minor corrections and additions have been made in the Appendices.
Adelaide, 1994 Martin Simons
The publication of Model Aircraft Aerodynamics in 1978 filled a gap not only in the literature for model fliers but on the shelves of many school and college libraries. The book has proved useful to designers of man-powered aircraft, ultra-light aeroplanes and gliders. Professional aeronautical engineers, researchers and academics, especially those involved with the development of (subsonic) remotely piloted vehicles, found the survey of boundary layer problems contained in the chapters on scale effects and low speed aerofoils particularly valuable as an introduction to this aspect of the subject.
Demand for the book justified several reprints. In the English language at least, it remains the only work of its kind in the field.
The general model aircraft scene has changed remarkably since 1978. Very large models have become almost commonplace. Many of them exceed the old legal limitations and have to be specially licensed for flight. Radio controlled helicopters have become reliable and sophisticated. The emphasis on multi-task and cross country flying for model sailplanes has transformed these aircraft beyond recognition, in ways that were only hinted at in the first edition. Every aspect of model design and construction has been profoundly affected by the increasing use of materials such as carbon fibre, Kevlar, and new kinds of adhesives. Radio control equipment now commonly available is extraordinarily precise and highly reliable. Electric and solar powered models flourish everywhere and begin to rival ‘glow plug’ engined craft. Further developments in gyroscopic stabilising devices and automatic pilots will make these more accessible in future and there is increasing interest in the development of advanced electronic instruments which will inform the pilot, on the ground, of exactly what his model is doing aloft. Microcomputers, now so commonplace, enable modellers, even without scientific or mathematical training, to design new aerofoil sections and optimise the performance of their aircraft by using commercially available software. Models already fly with small computers on board, not to mention surveillance instruments and cameras.
The need for a new edition of this book became increasingly apparent as die years passed. The basic theory has not changed, but the author has corresponded with many model fliers in many countries. These discussions have indicated to him some passages which were ambiguous or over-simplified in the original. There have been numerous small improvements of wording in the interests of greater clarity and emphasis. Some chapters have been re-grouped or re-arranged to improve the logical sequence. Many more sub-headings have been added to break up and make more legible what is, inevitably, a fairly solid text.
Substantial re-writing has been done in the chapter on trim and stability, not because the first edition was wrong but because a more emphatic statement seems necessary in an. area where much confusion remains even among very experienced modellers.
I A new section on winglets and tip sails has been included. The veiy brief notes about
wind tunnel testing (in the first edition only part of an Appendix) have now been expanded to a full chapter with some advice on the use of the data coming from various small wind tunnels now operating in several countries.
A new chapter on propellers has been added, since their omission from the first edition drew some criticism. It must still be admitted that a full treatment of this subject would require a different book, but, since the adoption of the turbo-jet engine for full-sized aircraft, there is a notable dearth of modem textbooks on the basic principles of propeller design. Some of the most prestigious libraries consulted were unable even to find the basic works on propellers which, once, were required reading for every student of aeronautics. The need for a very simple explanation seems quite pressing, and in a very limited space, it has been attempted here.
Helicopters too, require books to themselves, yet very little about the aerodynamics of rotors has appeared in a form suitable for the model flier. The final chapter of this edition can pretend to be nothing more than an outline sketch of some theoretical aspects of these extremely complicated devices. It may at least point the interested reader in the right general direction for further studies.
Apart from these changes, wherever possible the results of recent research have been incorporated in amplification and confirmation of the text. Much still remains to be investigated.
London 1986 Martin Simons
The author wishes to thank the many people who helped, sometimes without their knowing it, in the preparation of this book and the new edition. Some of them are aeromodellers whose questions and comments suggested the need for such a work in the first place. Since the publication of the first edition there has been much correspondence and many discussions with model fliers. The author has spoken and answered questions at a good many meetings, formal and informal, at places as far apart as rainswept hilltops in England and dry paddocks in Australia. It is hoped the revised text will stimulate as much thought and interest as the original did. Special thanks are owed to those who challenged some of the statements made or pointed to obscure passages requiring better wording.
Among the constructive critics who have helped with preparation of the revised edition are Noel Falconer, who supplied several pages of most valuable written commentary, Stan Hinds, Freddy Jones and Hans-Julius Schmidt. The new text should accommodate their points. Frank Irving’s kind assistance with the first edition has not been forgotten.
Thanks are owed again to Professor Eppler and Professor Wortmann (who died, most sadly, in 1985), and to Dr. Althaus, for permission to use some of their most recent research material. Rolf Girsberger supplied ordinates of his latest aerofoils for inclusion in Appendix 3. Thanks are also due to Michael Selig and Martin Hepperle.
Ron Moulton encouraged the author at all stages in preparation of the first two editions. Thanks are due now also to Beverly Laughlin and Lyn Corson of Argus Books for their help with the third edition.













 verticaI component opposing lift
verticaI component opposing lift