A first-order tensor (vector) x is the aggregate of ordered triples, any two of which satisfy the transformation law:
MB = [T]BA[xA (2.3)
where ]A and ]B are any allowable coordinate system.
A second-order tensor (tensor) X is the aggregate of ordered 9-tuples, any two of which satisfy the transformation law:
Щв = [T]BA[X|A[f]M (2.4)
where ]A and ]B are any allowable coordinate system.
By aggregate I mean the collection of all possible transformations among all allowable coordinate systems. That class could contain as many as oo2 elements: an infinite number for every frame over infinite numbers of frames.
How useful is this definition with infinite components? We can take two viewpoints:
1) Physical point of view—Tensors describe properties of intrinsic geometrical or physical objects, i. e., objects that do not depend on the form of presentation (coordinate system).
2) Mathematical point of view—Because tensors are the total aggregate of all ordered n-tuples, they are defined in all coordinate systems and thus are not tied to any particular one.
As we model aerospace systems, we deal with the physical world. Therefore, I adopt the physical point of view in this book and interpret these definitions in an intrinsic or invariant sense. The physical quantities exist a priori, with or without coordinates. The introduction of coordinates is just an expedience for numerical evaluation.
|
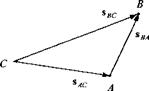
Fig. 2.2 Vector triangle.
|
A scalar is a particularly simple tensor. It remains the same in any allowable coordinate system, a useful characteristic that will serve us well in many proofs. We define a scalar as a physical quantity without any directional content, like mass, density, or pressure. Even particles and points belong in this category.
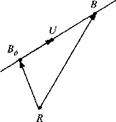
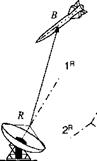
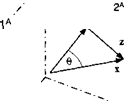
Some examples should clarify these definitions. Let us begin with the concept of a point and ask the question how do we determine its position? A point can have any position in space, or better, a point has no position unless related to another point, an intuitive postulate that follows from the Galilean relativity principle. The statement “I stand on the moon” uses the moon as reference. By just asserting “I stand,” nothing meaningful has been conveyed. Suppose I am modeled by point В and the footprint of Neil Armstrong is point A. Then my displacement from A is given by the vector s BA, and the displacement of the footprint with respect to me is sab – Both are related by sba = — sAb • Notice the important Rule 1: Subscript reversal changes the sign. If Michael Collins, at point C, wants to determine my position sbc and he knows the displacement of the footprint from him sac, and my displacement from the footprint sba, he can add the vectors to obtain the result (Fig. 2.2):
sbc = sba+sac (2.5)
Rule 2 becomes evident: Vector addition is by subscript contraction. The subscripts A are deleted to get the BC sequence
ВС <- В A+A C
contraction
Notice also the location of the arrowheads in Fig. 2.2. They are always at the first point of the subscript. The displacement of point В wrt point C is sвс with the arrowhead at point В.
To describe this scenario, there was no need to refer to any coordinate systems. We modeled the three entities by points and related them by invariant displacement vectors. For numerical evaluation, however, we have to choose coordinate systems. Suppose Collins wants to use a coordinate system ]c associated with his frame of reference. He expresses all terms in Eq. (2.5) by ]c coordinates
[SfidC = [Sba]C + t*Ac]C (2.6)
However, my displacement from the footprint is given in a coordinate system ]B, associated with my reference frame B. He therefore transforms my coordinates from ]B to ]c using the transformation matrix [T]CB according to Eq. (2.3):
|
– 2a
Fig. 2.3 Radius vector.
|
and substitutes the known coordinates into Eq. (2.6):
[Sficf = [T]Cfi[sBA]B + [sAC]c
If Collins knows the transformation matrix [ T]CB, he can compute my position in his coordinates.
Suppose his calculation furnishes [sic]c = [30,100 —1,500 2,800] km (I use the transposed to conserve space). To interpret the result, he has to know the direction and positive sense of the coordinate axes. If Iе is forward, 2C right, and 3C down, then the numbers would indicate to him that I am 30,100 km in front of him; 1,500 km to the left; and 2,800 km below. Please observe an important fact: no mention of a coordinate system origin was made. The numbers make perfect sense without Collins being at the origin. You may be shocked, but here is Rule 3: Coordinate systems have no origins.
Without origins, we have to dispose of radius vectors. They are used in vector mechanics to locate points in coordinate systems. But by doing so, the origins are made reference points. Because coordinate systems are purely mathematical entities, we cannot intermingle such physical reference points.
I will show that radius vectors are not vectors in the sense of the first-order tensor definition Eq. (2.3) and therefore cannot be part of our toolbox. Displacement vectors, on the other hand, are legitimate tensors.
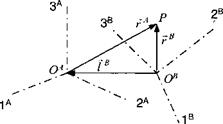
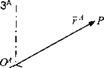
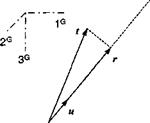
Figure 2.3 depicts the radius vector rA emanating from the origin Oa of the coordinate system A to the point P. Two radius vectors associated with two coordinate systems A and В are related by the vector addition rR =rA +lB, where lB is the radius vector of the origin 0A, referenced in the В coordinate system (see Fig. 2.4). With [TBA the transformation matrix of coordinates В wrt A, the radius vector rA in coordinate system A transforms to the radius vector rB in coordinate
|
3A P
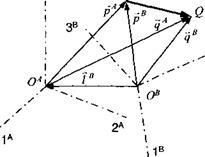
Fig. 2.5 Displacement vector.
|
system B, as follows:
|
Kl
|
|
~hi
|
t2
|
hi
|
|
|
|
Гів1
|
|
4
|
=
|
hi
|
*22
|
*23
|
|
4
|
+
|
lB
l2
|
|
1— •ч
wCe
l_
|
|
-hi
|
*32
|
*33_
|
|
4
|
|
lB
L(3 J
|
and the abbreviated matrix notation
[rB]B = [T]BA[rAf + [if (2.7)
Compare this transformation with the transformation that defines a tensor Eq. (2.3). Because of the additional term [If, the radius vector rA does not transform into rB like a first-order tensor and therefore is not a tensor.
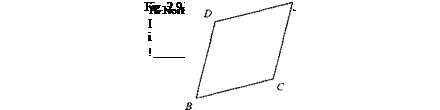
Conversely, let us prove that displacement vectors are tensors. Introduce the vector sqp as the displacement of point Q wrt point P, as shown in Fig. 2.5. It is related to the radius vector of coordinate system A by
[sQpf = [qAt ~ [pAf (2.8)
and to those of coordinate system В by
[sQpf = [qBf – [pBf (2.9)
The radius vectors [qBf and [pBf transform according to Eq. (2.7):
[qBf = [TfA[qAf + [If [pBf = [TfA[pAf + [If
Substituting these into Eq. (2.9) and with Eq. (2.8) yields
Indeed, the displacement vector Sqp transforms like a first-order tensor
[sQP]B = [T]ba[sqp]a
and therefore is a tensor.
I hope that you appreciate now the difference between radius and displacement vectors. Because we want to use only invariant tensor concepts, I have to give Rule 4: Radius vectors are not used. Before we move on to geometrical applications, let us summarize the four rules.
Rule 1: Subscript reversal of displacement vectors changes their sign.
Rule 2: Vector addition of displacement vectors must be consistent with sub
script contraction.
Rule 3: Coordinate systems have no origins.
Rule 4: Radius vectors are not used.
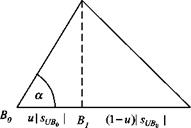
![]() usBR = const
usBR = const![]() const
const











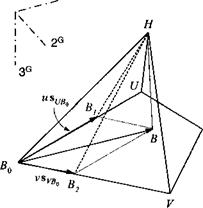
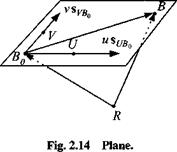
![Plane Подпись: [^c/fio]0 = ISUH]G + [sr/Bo] ; [WBO] — [WH]0 + [jvffio] [■Sfitf]0 = u [ri/fi,, ] + + K«]](/img/3132/image041_1.gif)
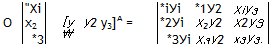
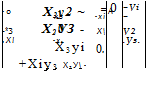
 У202 + 102 + (-9)У302 + (-20)2 + (—9)2
У202 + 102 + (-9)У302 + (-20)2 + (—9)2