Category Modeling and Simulation of Aerospace Vehicle Dynamics

Coordinates are ordered algebraic numbers called triples or n-tuples. Coordinate systems are abstract entities that establish the one-to-one corre­spondence between the elements of the Euclidean three-space and the coordinates.

Cartesian coordinate systems are coordinate systems in the Euclidean space for which the Cartesian metric As2 = JT &xf holds.

Coordinate axes are the geometrical images of mathematical scales of algebraic numbers.

Coordinate transformation is a relabeling of each element in Euclidean space with new coordinates according to a certain algorithm. A coordinate system is said to be associated with a frame if the coordinates of the frame points are time invariant. All coordinate systems embedded in one frame form a class X. All classes over all frames form the entity of the allowable coordinate systems.

These definitions necessitate some explanations. Coordinates are arranged as num­bered elements of matrices, e. g., the coordinates of the velocity vector v! B, ex­pressed in the Earth coordinate system }E, are

Kf =

The triple occupies three ordered positions in the column matrix. The moment of inertia tensor, expressed in the body coordinate system )B, exhibits the 9-tuple of ordered elements

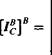in in iз /21 hi І23 hi hi hs_

By the way, not every matrix and its elements constitute the coordinates of a ten­sor. There must exist a one-to-one correspondence between the three-dimensional

Euclidean space and the coordinates. For instance, the three velocity coordinates are related to the three orthogonal directions of Euclidean space by

The moment of inertia tensor, on the other hand, has two directions associated with each element.

Because we are dealing with physical quantities, their numerical coordinates imply certain units of measure. The same units are embedded in every coordinate, e. g., v і, l’2, and t>3 all have the units of meters per second. This requirement to give measure to the coordinates leads to the geometrical concept of coordinate axes. They can be envisioned as rulers, etched with the unit measures, and given a positive direction.

At this point we pause and compare coordinate systems with frames of ref­erence. We defined a frame as a physical entity, consisting of points without relative movement. On the other hand, coordinate systems are mathematical ab­stracts without physical existence. This distinction is essential. Let me again quote Truesdell,3 “It is necessary to distinguish sharply between changes of frame and transformation of coordinate systems.” This separation will enable us to model the dynamics of flight vehicles in a coordinate-independent form, using points and frames, and defer the coordination and numerical evaluation until the building of the simulation.

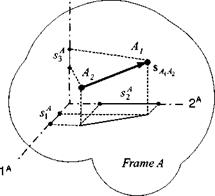
Let us explore this conversion process. Given frame A and two of its points A) and A2 (see Fig. 2.1), the displacement vector of point A1 wrt A2 is sAlAl. This vector is a well-defined quantity without reference to a coordinate system. Now we create a Cartesian coordinate system that establishes one-to-one relationships between the three-dimensional Euclidean space and the coordinates of the dis­placement vector. Designating it by ]A, we have one particular matrix realization

3A

of the displacement vector

The coordinates are shown in Fig. 2.1, superimposed on the coordinate axes. We label the axes in the 1 – 2 – 3 sequence with the name of the coordinate system as superscript. If the coordinates do not change in time, the coordinate system ]A is said to be associated with frame A. There are many, actually an infinite number of coordinate systems that have the same characteristic. They form a class K, the so-called associated coordinate systems with frame A.

Moreover, there are other coordinate systems. Picture a spear A, whose center – line is modeled by the displacement vector вд, д2, with point Ai marking the tip and A2 the tail. We already discussed the coordinating in the associated coordi­nate systems of its frame A. But suppose, you as observer, modeled by frame B, watch the spear in flight. In a coordinate system ]B associated with your frame, the centerline would have the coordinates

[*а, а2]В =

However, the coordinates are now changing in time. Your frame has a whole class К of such coordinate systems, just like the frame of the spear. There could be many frames (persons) present. All of these classes of coordinate systems form an entity, called the allowable coordinate systems.

Converting from one coordinate system to another is a relabeling process:

Because our coordinate systems are Cartesian, the relabeling algorithm is the multiplication of a 3 x 3 matrix with the coordinates of the vector

We symbolize the transformation matrix by [T]BA, meaning that it establishes the ]B coordinates wrt the]A coordinates. Notice my strict adherence to the double­index convention, reading from left to right, В —*■ A, and linking them with the words with respect to. Equation (2.1) is abbreviated by

[sa, a2]B = тВА[*д, д2]А (2.2)

The substance of the spear has not changed. We just have expressed the coordinates

of its centerline in two different coordinate systems. If the coordinate systems are associated with frames that change attitude relative to each other, the elements of T{t)BA are, as in our spear example, a function of time. Only if they are part of the same frame or other fixed frames are the elements constant.

By convention and convenience we use only right-handed Cartesian coordinate systems. (This terminology refers to the motion of the right hand, symbolically rotating the 1-axes into the 2-axis—shortest distance—while the index finger points in the positive direction of the З-axis.) We use them exclusively because they have the pleasant feature of their determinants always being positive one and their inverse equaling the transpose.

The discussion of Euclidean space would be incomplete without mentioning other coordinate systems that satisfy the Euclidean metric. Best known among them are the cylindrical and spherical coordinates. They are also orthogonal in the infinitesimal small sense of the Euclidean metric. However, only Cartesian coordi­nates satisfy the finite orthogonality of the Cartesian metric within the Euclidean space. With the definition of Cartesian coordinate systems in place, we can finally turn to the definition of tensors.

We attribute tensor calculus to the Italian mathematicians Ricci and Levi-Civita,4 who provided the modeling language for Einstein to formulate his famous General Theory of Relativity.5 More recently, tensor calculus is also penetrating the applied and engineering sciences. Some of the references that shaped my research are the three volumes by Duschek and Hochrainer,6 which emphasize the coordinate invariancy of physical quantities; the book by Wrede,7 with its concept of the rotational time derivative; and the engineering text by Betten.8

The world of the engineer is simple, as long as he remains in the solar system and travels at a fraction of the speed of light. His space is Euclidean and has three
dimensions. Newtonian mechanics is adequate to describe the dynamic phenom­ena. In flight mechanics we can even further simplify the Euclidean metric to finite differences Л, the so-called Cartesian metric

з

As2 — Ax2 + Ax + Ax2 = ^2 &хї

/=1

The elements Дх, are mutually orthogonal, and the metric expresses the Pythagorean theorem of how to calculate the finite distance As. In this world tensors are called Cartesian tensors. As we will see, they are particularly simple to use and completely adequate for our modeling tasks.

The elements of Cartesian tensor calculus are few. I will summarize them for you, discuss products of tensors, and wrap it up with some examples. Keep an open mind! I will break with some traditional concepts of vector mechanics in favor of a modem treatment of modeling of aerospace vehicles. Before we discuss Cartesian tensors however, we need to define coordinates and coordinate systems.

Now we come to a nettlesome issue. What notation is best suited for modeling of aerospace vehicle dynamics? It should be concise, self-defining, and adaptable to tensors and matrices. By “self-defining” I mean that the symbol expresses all char­acteristics of the physical quantity. For intricate quantities it may require several sub- and superscripts.

Surveying the field, I go back to my vector mechanics book. There, as an ex­ample, velocity vectors are portrayed by symbols like v, v, v, or v. An advanced physics book will most likely use the subscripted tensor notation, emphasizing the transformation properties of tensors. The velocity vector is written as u,; і =

1,2,3 over the Euclidean three-space, and the transformation between coordinates is

vi=tijVj j — 1,2,3; і = 1,2,3

with the summation convention over the dummy index j implied, meaning

Draper Laboratory at the Massachusetts Institute of Technology has modified this convention, favoring the form

Vі =tljvj; j = 1,2,3; і = 1,2,3

as a vector transformation.

Our need is driven by our modeling approach, i. e., from invariant tensors to programmable matrices. Vector mechanics emphasizes the symbolic, coordinate – independent notation, whereas the tensor notation focuses on the components. We adopt the best of both worlds. Bolded lower-case letters are used for vec­tors (first-order tensors) and bolded upper-case letters for tensors (second-order tensors). For scalars (zeroth-order tensor) we use regular fonts. These are the only three types of variables that occur in the Euclidean space of Newtonian mechanics.

The sub- and superscript positions immediately after the main symbol are re­served for further specification of the physical quantity. Here we make use of our postulate that points, and frames suffice to describe any physical phenomena in flight dynamics. We fix indelibly the following convention: subscripts for points and superscripts for frames. For both we use capital letters. Some examples should crystallize this practice.

The displacement vector of point A with respect to point В is the vector sAb the velocity vector of point В with respect to the inertial frame I is modeled by v ; and the angular velocity vector of frame В with respect to frame / is annotated by u>BI. All three are first-order tensors. The moment of inertia tensor IB of body (frame) В referred to the reference point C is a second-order tensor. If there are two sub – or two superscripts, they are always read from left to right, joined by the phrase “with respect to” (wrt).

For expressing the tensors in coordinate systems, we could use the subscript notation of tensor algebra or the sub/superscript formulation of the Massachusetts Institute of Technology. However, our sub – and superscript locations would become overloaded. I prefer to emphasize the fact that the tensor has become a matrix (through coordination) by using square brackets with the particular coordinate system identified by a raised capital letter. Let us expand on the four examples.

To express the displacement vector sAB in Earth coordinates E, we write [л’дд]£; the velocity vector Vg becomes [v’H |£; and the angular velocity vector u>BI, stated in inertial coordinates, is [ ooBI]1. All three are 3×1 column matrices. The moment of inertia tensor IB, expressed in body coordinates B, is the 3 x 3 matrix [IB]B■ Usually the bolding of the symbols will be omitted once the variable is enclosed in brackets, and we will write plainly [sAB]E, [v’BE, [coBI]1, and [IB]B.

The nomenclature at the front of this volume summarizes most of the variables that you will encounter throughout the book. I will adhere to these symbols closely, only changing the sub – and superscripts. Let me just point out a few things. All variables are considered tensors either of zeroth-, first-, or second order, but I will use mostly the term vector for the first-order tensor. The transpose is indicated by an overbar. We will distinguish carefully between an ordinary and rotational time derivative.

The advantage of the nomenclature lies in the clear distinction between coordinate-independent (invariant) tensor notation and the coordinate-dependent bracketed matrix formulation. General tensor algebra, with its sub – and superscript notation, emphasizes many types of tensors, e. g., covariant, contravariant tensors, Kronecker delta, and permutation symbol. The dummy indices and contraction (summation) play an important part. This mathematical language was created for the sophisticated world of general relativity embedded in Riemannian space. Our world is still Newtonian and Euclidean. Simple Cartesian tensors are completely adequate. Therefore, I forego the tensorial sub – and superscript notation in favor of the matrix brackets and am able to readily distinguish between the many coordinate systems of flight mechanics.

With the general principles of classical mechanics under our belt, we employ a mathematical language that allows us to formulate dynamic problems concisely and to solve them readily with computers. We make use of two fundamental mathematical notions: Points are mathematical models of a physical object whose spatial extension is irrelevant. Frames are unbounded continuous sets of points over the Euclidean three-space whose distances are time invariant and which possess a subset of at least three noncollinear points.

Points and frames, although mathematical concepts, are regarded as idealized physical objects that exist independently of observers and coordinate systems. A point designates the location of a particle, but it is not a particle in itself. It does not have any mass or volume associated with it. For instance, a point marks the c. m. of a satellite; but for modeling the dynamics of the trajectory, the satellite’s mass has to join the point to become a particle. Only then can Newton’s second law be applied.

Combining at least three noncollinear points, mutually at rest, creates a frame. The best known frames are the frames of reference. Any frame can serve as a frame of reference. We will encounter inertial frames, Earth frames, body frames, and others. A frame can fix the position of a rigid body, but it is not a rigid body in itself. Only a collection of particles, mutually at rest, forms a rigid body. It is essential for you to remember that both, points and frames, are physical objects, albeit idealized.

Points and frames are the building blocks for modeling aerospace vehicle dy­namics. I will show by example that they are the only two concepts needed to formulate any problem in flight dynamics. Surprised? Follow me and you be the judge and jury.

We need a mathematical shorthand notation to describe points and frames and their interactions in space and time. Tensors in their simple Cartesian form will serve us splendidly. They exist independently of observers and coordinate systems, and their physical content is invariant under coordinate transformations.

Coordinate systems are required for measurements and numerical problem solv­ing. They establish the relationship between tensors and algebraic numbers and are a purely mathematical concept. Be careful however! Truesdell3 warns, “In particular, frame of reference should not be regarded as a synonym for coordinate system.” They are two different entities. Frames model physical objects, while coordinate systems embed numbers, called coordinates.

These coordinates are ordered numbers, arranged as matrices. Matrices are algebraic arrays that present the coordinates of tensors in a form that is convenient for algebraic manipulations. You will build simulations mostly from matrices. Computers love to chew on these arrays.

The modeling chain is now complete. The mathematical modeling of aerospace vehicles is a three-step process: 1) formulation of vehicle dynamics in invariant tensor form, 2) introduction of coordinate systems for component presentation, and 3) formulation of problems in matrices for computer programming and numerical solutions.

First, you have to think about the physics of the problem. What laws govern the motions of the vehicle? What are the parameters and variables that interact with each other? Which elements are modeled by points and which by frames? Then introduce tensors for the physical quantities and model the dynamics in an invariant form, independent of coordinate systems. Manipulate the equations until they divulge the variables that you want to simulate.

As a physicist you would be finished, but as an engineer your toil has just begun. You have to select the proper coordinate systems for numerical examination. What coordinate systems underlie the aerodynamic and thrust data? In what coordinates are the moments of inertia given? Does the customer want the trajectory output in inertial coordinates or in longitude and latitude? There are many questions that you have to address and translate into the mathematical framework of coordinate systems.

Eventually all equations are coordinated and linked by coordinate transforma­tions. The tensors have become matrices and are ready for programming. Any of the modem computer languages enable programming of matrices directly or at least permit you to create appropriate objects or subroutines. Finally, building the simulation should be straightforward, although very time consuming.

Material bodies consist of matter whose behavior is modeled by constitutive equations. Because it is impossible to capture all of the nuances, special ideal materials are devised that approximate the phenomena. Their behavior is governed by constitutive equations.

When I searched the literature for basic modeling principles of material bodies, I found a very useful account by Noll2 on the invariancy of constitutive equa­tions. It was enshrined later in the new edition of the Handbuch der Physik, jointly authored by Tmesdell and Noll.3 These constitutive equations satisfy three principles:

1) Coordinate invariance: Constitutive equations are independent of coordinate systems.

2) Dimensional invariance: Constitutive equations are independent of the unit system employed.

3) Material indifference: Constitutive equations are independent of the observer. Or expressed in other words, the constitutive equations of materials are invariant under spatial rigid rotations and translations.

Material interactions do not depend on the coordinate system used for their numerical evaluations. As an example, the airflow over an aircraft wing and the resulting pressure distribution exist a priori, without specification of a coordinate system. You could record it in aircraft coordinates or, via telemetry, in ground coordinates. In both cases you would calculate the same lift. Or consider the thrust vector of a turbojet engine. It could be measured in aircraft or engine coordinates. The resultant force is still the same.

Does it matter whether you use metric or English strain gauges to record the thrust? You will get different numbers, but certainly the aircraft responds to the thrust unfettered by human schemes of measuring units. Physical phenomena tran­scend the artificiality of units.

The principle of material indifference, or, more precisely, the principle of mate­rial /rame-indifference, as Truesdell and Noll3 call it, is tantamount to the general theory of material behavior. It asserts “that the response of a material is the same for all observers.”3 Let the captain delight in the bulge of the sails or a dockside bystander conclude that a stiff easterly blows. Their emotions may be different, but, nevertheless, the bulge has not budged.

You may be part of an international calibration team. You take that norm-sphere and measure its drag in the wind tunnel at the University of Florida and then travel to Stuttgart, Germany, and repeat your test. If the measurements differ, you would not explain the discrepancy by the fact that the facilities are separated by 4000 miles and tilted by 67 deg with respect to each other (different longitude and latitude); rather, you would look for physical differences in the tunnels.

The Principle of Material Indifference (PMI) is the cornerstone of mathemati­cal modeling of dynamic systems. It will enable us to formulate the equations of motions of aerospace vehicles in an invariant form and serve us to prove several theorems.

Classical mechanics is the investigation of the interactions of material bodies and forces in Euclidean space-time. According to Hamel it is governed by four axioms[1]:

2) Space is isotropic. There exists no preferred direction in space.

3) Every effect must have its cause by which it is uniquely determined. This is also called the causality principle.

4) No particular length, velocity, or mass is singled out.

Homogeneity of space is not natural to us. We think we are at the center of the universe and everything else turns around us. Yet we are just one reference frame. Every person can make the same claim. Homogeneity expresses the fact that all reference frames are equally valid, and therefore there is no preferred location in space. Does the sun revolve around Earth or Earth around the sun? Either statement is valid. It is just a matter of reference.

Homogeneity of time means that there exists no preferred instant of time. In the western world the Julian calendar begins with the birth of Christ, but other civilizations have their own calendars with different starting times. These are just arbitrary man-made beginnings. However, because time is a uniformly increasing measure, it must have had a beginning. That instant, when time was created, is distinct, but we do not know when it occurred. All other times have equal stature.

Space is not only homogeneous, but also isotropic, meaning that all directions in space have equal significance. On Earth we fly by the compass, which indicates magnetic north. But Mars probes navigate in an inertial, sun-centered frame, which is unrelated to terrestrial north. These are man’s preferences. Space itself has no preferred direction.

We all have experienced the causality principle in our lives. I cut my finger (cause), and blood drips (effect). The pilot increases the throttle, the engine in­creases thrust, and the aircraft gains speed or altitude. There are two effects possi­ble, speed and altitude, but each is uniquely determined by the thrust increase. All laws of classical mechanics abide by this causality principle.

The fourth axiom is a source of distress for all of those scientists who have tried for centuries to define the length of a meter. Eventually they agreed to make two marks on a bar of platinum and store it at the Bureau International des Poids et Mesures near Paris at a temperature of 0°C. There you also find the kilogram, well preserved for those who cherish precision. Yet, classical mechanics does not recognize any of these human endeavors.

Modem physics brakes with tradition and violates at least one of these axioms. In relativistic mechanics space is inhomogeneous and nonisotropic (Riemannian space); quantum mechanics does not recognize the causality principle; and the theory of relativity singles out the speed of light.

So confident were the researchers that Hamel would write in the 1920s in the famous Handbuch der Physik} an axiomatic treatment of mechanics—an axiom is a statement that is generally accepted as self-evident troth. I follow Hamel’s lead

and delineate the basic elements of classical mechanics:

1) Material body: A body is a three-dimensional, differentiable manifold whose elements are called particles. It possesses a nonnegative scalar measure that is called the mass distribution of the body. In particular, a body is called rigid if the distances between every pair of its particles are time invariant.

2) Force: The force describes the action of the outside world on a body and the interactions between different parts of the body. We distinguish between volume forces and surface forces.

3) Euclidean space-time: The interaction of the forces with the material body occurs in space and time and is called an event. Events in classical mechanics occur in Euclidean space-time. The Euclidean space exhibits a metric that abides, for infinitesimal displacements d. s, the law of Pythagoras over the three-dimensional space {xі, X2, хз):

з

dsz = dx + dxj + dx — ^ dxf

i=l

The concept of a particle, so important in classical mechanics, defines a math­ematical point with volume and mass attached to it. We could also call it an atom or molecule, but prefer the mathematical notion to the physical meaning. By accu­mulating particles we form material bodies with volume and mass. If the particles do not move relative to each other, we have the all-important concept of a rigid body.

Without forces, the body would, according to Newton’s first law, persist at rest or continue its rectilinear motion. However, we shall have plenty of opportunity to model forces. There are aerodynamic and propulsive forces acting on the out­side of the body as surface forces. We will deal with gravitational effects, which belong to the volume forces, acting on all particles, and not only on those at the surface.

In classical mechanics space and time are entirely different entities. Space has three dimensions with positive and negative extensions, but time is a uniformly increasing measure. For us, this so-called Galilean space-time model will suffice. However, we should remember that in 1905, just after the turn of the century, Albert Einstein revitalized physics with his Special Theory of Relativity, where time becomes just a fourth dimension.

Einstein did not abolish Newton’s laws, but expanded the knowledge of space and time. He relegated Newton to a sphere where velocities are much less than the speed of light. However, that sphere encompasses all motions on and near the Earth. Even planetary travel is adequately represented by Newtonian dynamics, consigning relativistic effects to small perturbations.

Modeling is a broad term with many meanings. Would it not be more exciting if this were a book about fashion models and a collection of pretty pictures? Well, a model is something uncommon or unreal. It is the copy of an object. The objects that I will focus on are inert, but nevertheless exciting. We are dealing with aircraft, spacecraft, and missiles. However, instead of building scaled replicas of these ve­hicles, we construct mathematical models of their dynamic behavior. Launching models is always more fun than just having them sitting on your shelf. I will teach you how to make them soar on your computer. But first we have to lay the founda­tion. Classical mechanics, a branch of physics, will be our cornerstone. Digging deep into the past, I found an interesting axiomatic treatment of the principles of mechanics. It will serve us well when we lay out the canon of modeling. Partic­ularly useful is the principle of material indifference, which we will employ for several proofs.

The mathematical language we use consists of tensors and matrices. That may get you excited, but calm down—the bare essentials of Cartesian tensors will suffice. We will talk about frames, coordinate systems, transformation matrices, and so on, in a systematic order. If you are rusty in matrix algebra, brush up with Appendix A.

Of course, all theory is only as good as it is able to solve practical problems; at least that is the opinion of most engineers. I subscribe to that philosophy also and will show you in this chapter just how well tensors model geometrical problems. Throughout this book they will be our companions. Our motto is “from tensor modeling to matrix coding.” Thus, expand your mind and go back to explore the future!

2.1 Classical Mechanics

At the turn of the last century, physicists thought that all of the laws of the physical universe were known. Over three centuries, Galileo, Newton, Bernoulli, D’Alembert, Euler, and Lagrange built the structure of the branch of physics that we call mechanics. Today, after another century of breathtaking progress in the physical sciences, we fondly remember that fully developed branch as classical mechanics. Although physicists have turned their back on it, engineers have ex­plored it through many adventures, from first flight to a visit to the moon.

Having mastered the skills of modeling, you are prepared to face the challenge of simulation. The venture is not of a theoretical nature but one of encyclopedic knowledge of the subsystems that compose a flight vehicle. Who can claim to be an expert in aerodynamics, propulsion, navigation, guidance, and control all together? To be a good simulation engineer, however, you must be at least acquainted with all of these disciplines. In Part 2,1 will expose you to these topics at increasing levels of sophistication. As we proceed from three – to six-DoF simulations, the prerequisites increase. You may have to do some background reading to keep up with the pace. Yet, let me also caution you that my treatment of subsystems is incomplete and that you must foster good relationships with experts in these fields to gain access to more detailed models.

Seldom will you be called to develop a simulation ex nihilo. Somebody has trodden that path before, and you should not hesitate to follow in his footsteps. At least pick up the outer shell, consisting of executive and input/output handling. A good graphics and postprocessing capability is also important. Then you can fill in the subsystem models and build your own vehicle simulation. But scrutinize the borrowed code carefully. Once you deliver your product, then you will be responsible for the entire simulation.

There are quit a few simulation environments you can choose from. They are categorized by programming language. Most mature simulations are based on FORTRAN with many years of verification and validation behind them. A new crop of symbolic simulations has emerged, e. g., VisSim™, MATLAB®, and Simulink®, which use interactive graphics for modeling and code generation for executable C programs. That development has spawned another trend, namely pro­gramming simulations in C++ directly, the language of choice for most developers today.

I seized on the enormous flexibility of C++ and created a new aerospace sim­ulation environment called CADAC++ (Computer Aided Design of Aerospace Concepts in C++). Over the years it grew from simple three-DoF simulations to sophisticated six-DoF hypersonic vehicle models. Appendix C details the source code that is available in my three AIAA Self Study CD-ROMs.

However, CADAC in its original FORTRAN makeup is still the favored simu­lation environment for this book because of its straightforward implementation. It consists of three-, five-, and six-DoF aerospace simulations. They are provided on the CADAC CD-ROM, which also includes plotting and analysis programs. For a quick start, follow the CADAC Primer in Appendix В.

Table 1.1 lists the prototype simulations. They encompass a broad selection of models from three to six DoF, from flat to elliptical Earth, from drag polars to full aerodynamic tables, from rocket to ramjet propulsion, and from simple to complex flight control systems. The number of lines of code gives you an idea of the size of the subroutines that model the subsystems of the vehicles.

Because practice makes perfect, you should attempt to carry out the projects at the end of Chapters 8-10. The required data are on the CADAC CD. As you exercise your modeling skills, you add to you repertoire the simulations listed in Table 1.2: SST03 highlights the importance of trajectory shaping; AGM5 is an adaptation of the AIM5 simulation for the air-to-ground role; FALCON5 combines trimmed FALCON6 aerodynamics with the navigation aids of CRUISE5; and AGM6 is a detailed air-to-ground missile.

All of these simulations support the discussion of subsystem modeling, although the derivations in Chapters 8-10 are self-contained and apply to any simulation environment. We shall revisit the equations of motion, cover many aerodynamic modeling schemes, discuss all types of propulsion, design autopilots, and pro­vide navigation and guidance aids where needed. Each chapter is devoted to one particular type of simulation.

The eighth chapter, “Three-Degrees-of-Freedom Simulation,” models point – mass trajectories. The three translational degrees of freedom of the c. m. of the vehicle are derived from Newton’s second law for spherical rotating Earth and expressed in two formats. The Cartesian equations use the inertial position and velocity components as state variables, whereas the polar equations employ geo­graphic speed, azimuth, and flight-path angles.

Here I introduce the environmental conditions, which are applicable to all sim­ulations. The three most important standard atmospheres, ARDC 1959, ISO 1962, and US 1976, are compared. The analytical ISO 1962 model wins the popularity contest for simple endo-atmospheric simulations. Newton’s law of attraction pro­vides the gravitational acceleration. The term gravity acceleration is introduced for the apparent acceleration that objects are subjected near the Earth.

Aerodynamics is kept simple. Parabolic drag polars combined with linear lift slopes describe the lift and drag forces of aircraft and missile airframes. They

are expressed in coordinates of the load factor plane. We touch on all types of propulsion systems: rocket, turbojet, ramjet, scramjet, and combined cycle engines. Although simple in nature, the propulsion models are used in many simulations, from three to six degrees of freedom.

The ninth chapter, “Five-Degrees-of-Freedom Simulation,” combines the three translational degrees of freedom with two attitude motions, either pitch/yaw or pitch/bank. We make use of a simplification that uses the autopilot transfer func­tions to model the attitude angles. This feature, i. e., supplementing nonlinear trans­lational equations with linearized attitude equations, is called a pseudo-five-DoF simulation. As the examples show, it finds wide applications with aircraft and missiles.

These pseudo-five-DoF equations of motion are derived for spherical Earth and specialized for flat Earth. Because the Euler equations are not solved, the body rates are derived from the incidence rates of the autopilot and the flight-path angle rates of the translational equations. They are needed for the rate gyros of the inertial navigation systems (INS) and the rate feedback of gimbaled seekers.

Subsystems are the building blocks of simulations. I cover them at various lev­els of detail, either in Chapter 8, here, or in Chapter 10. Some of the treatment, especially aerodynamics and autopilots, is tailored to the type of simulation. How­ever, the sections on propulsion, guidance, and sensors are universally applicable. Table 1.3 lists the features available to you.

A detailed description of the AIM5 simulation concludes the chapter. It ex­emplifies a typical pseudo-five-DoF simulation. As you follow my presentation, you will discover how the angle of attack, as output of the autopilot, is used in the aerodynamic table look-up. The guidance loop, wrapped around the control loop, exhibits the key elements: a kinematic seeker, proportional navigation, and miss distance calculations. If you want to work a simple, but complete missile simulation, the AIM5 model is the place to start.

The tenth chapter, “Six-Degrees-of-Freedom Simulation,” explores the sophisti­cated realm of complete dynamic modeling. The three attitude degrees of freedom,

governed by Euler’s law, join Newton’s translational equations. Creating a six-DoF simulation is the ambition of every virtual engineer.

We ease into the topic with the derivation of the equations of motion for flat Earth and its expansions to spinning missiles and Magnus rotors. Afterward, we accept the challenge and consider the Earth to be an ellipsoid. An excursion to geodesy will expose you to the geodetic coordinate system and the second-order model of gravitational attraction. All will culminate with the six-DoF equations of motion for elliptical rotating Earth, complemented by the methods of quaternion and direction cosine for attitude determination.

The description of subsystems is continued from Chapter 9 and summarized in Table 1.4. Whereas aerodynamics, autopilots, and actuators are partial to six-DoF simulations, the remaining three topics of inertial navigation guidance and seeker apply also to five-DoF models. The best way to master these diverse subjects is by experimenting with simulations. You will find all features modeled at least in one of the simulations SRAAM6, FALCON6, or GHAME6.

Monte Carlo analysis is the prerogative of six-DoF simulations. Their high fi­delity, including nonlinearities and random effects, can only be exploited by a large number of sample runs, followed by statistical postprocessing. The methodology of accuracy analysis is discussed for univariate and bivariate distributions, with particular emphasis on miss-distance calculations.

Wind and turbulence is another field reserved for six-DoF models. With the stan­dard NASA wind profile over Wallops Islands and the classic Dryden turbulence model, you can investigate environmental effects on your vehicle design. Because of the stochastic nature of the phenomena, the Monte Carlo approach will yield the most realistic assessment.

The eleventh chapter, “Real-Time Applications,” gives you a taste of exploring the higher levels of the pyramid of Fig. 1.1. After having spent 10 chapters building the solid foundation of engineering simulations, you can lift your head and strive for piloted engagement simulations, hardware-in-the-loop facilities (HIL), or even participate in war games.

Flight simulators model the dynamic behavior of aerospace vehicles with human involvement. I discuss simple workstation and sophisticated cockpit simulators with their motion, vision, and acoustic environments. They find many uses, from control law development, flight-test analysis to pilot training.

When flight simulators are linked together, role playing can be staged. Blue fighters engage red aircraft, and blue and red missiles fly through the air. I will survey close-in air-to-air combat with its tactics and standardized maneuvers. Par­ticularly, I will discuss the need for high-fidelity missile models and the proper use of five – and six-DoF simulations. To simplify the validation process, a real-time conversion process is described that prepares a complete CADAC model for the flight simulator.

A HIL facility combines hardware with software and executes in real time without humans-in-the-loop. Although expensive to build, it is indispensable for flight hardware integration and checkout. Our discussion will be brief, highlighting the main elements of flight table, target simulator, and main processor. Some of the elements of HIL simulators like aerodynamics, propulsion, and the equations of motion have to be implemented on the processor. Yet seekers, guidance and control systems can be hardware or software based; it just depends on the maturity of the development program.

Finally, let the games begin! Wargaming is an old art that has experienced a renaissance of unprecedented scope. The U. S. Armed Forces try to outdo each other at their annual games: Army After Next, Global (Navy), and Global Engagement (Air Force). You will kibitz a typical scenario and see how war games are built, conducted, and evaluated. But it will hardly make you a commanding general.

We will be content building the foundational engineering simulations on which engagement, mission, and campaign models rest. This book is intended to be your guide for modeling flight dynamics and simulating aerospace vehicles, providing you with virtually everything you need to become a better virtual engineer.

Flight dynamics is the study of vehicle motions through air or space. Unlike cars and trains, these motions are in three dimensions, unconstrained by road or rail. Flight dynamics is rooted in classical mechanics. Newton’s and Euler’s laws are quite adequate to calculate their motions. Relativistic effects are relegated to miniscule perturbations.

An aerospace vehicle experiences six degrees of freedom. Three translational degrees describe the motion of the center of mass (c. m.), also called the trajectory, and three attitude degrees orient the vehicle. If the c. m. of the vehicle is used as
reference point, the translational and attitude motions can be described separately. Tracking a missile means recording the position coordinates of its c. m. Maintaining attitude of an aircraft requires the pilot to watch carefully the attitude indicator without reference to the aircraft’s position.

Newton’s second law governs the translational degrees of freedom and Euler’s law controls the attitude dynamics. Both must be referenced to an inertial reference frame, which includes not just the linear and angular momenta but also their time derivatives. As long as the coordinate system is inertial, the equations are simple, but if body coordinates are introduced additional terms appear that make the adjustments for the time-dependent coordinate transformations.

My goal is to model flight dynamics in a form that is invariant under time – dependent coordinate transformations. To that end, these additional terms must be suppressed. A time operator, the rotational time derivative, will accomplish this feat. With it we can formulate the equations of motion in an invariant tensor form, independent of coordinate systems.

To clarify that approach, let me use Newton’s second law as presented in any physics book. With p the linear momentum vector and/ the external force vector, the time rate of change of the linear momentum equals the external force

Implied is that the time derivative is taken with respect to the inertial reference frame I. If we want to change the reference frame to the vehicle’s body frame B, Newton’s law must be written

dp

d t

with u> the angular velocity of the body relative to the inertial frame. For pro­gramming, we have to coordinate the two equations. Because of the time deriva­tives, we express the first equation in inertial coordinates and the second one in body coordinates. Brackets and superscripts I or В indicate the coordinated vectors

-dpi1

d t

where [£2]B is the skew-symmetric form of ш, expressed in body coordinates. The time derivative is not a tensor concept because it changes its form as the inertial coordinates are replaced by the body coordinates. It is not invariant under the transformation matrix (T]B7 of the body coordinates with respect to the inertial coordinates, i. e., the right and left sides of the transformation are dissimilar:

If we introduce the rotational time derivative D1 relative to frame /, Newton’s law has the same form in both coordinate systems,

[.D>pY = uv

[D’p]B = [f]B

and the rotational time derivative transforms like a first-order tensor:

[D’p]B = [Tf^D’p]1

With [T]BI representing any, even time-dependent, coordinate transformations, Newton’s law can be expressed in the invariant tensor form

D’p = f (1.2)

valid in any coordinate system. This tensorial formulation is the key to the invariant modeling of flight dynamics. It will allow us to derive the mathematical model first without consideration of coordinate systems. After having made desired changes, we pick the appropriate coordinate systems and code the component form.

The motto “from tensor modeling to matrix coding” will guide us through kinematics and dynamics to the simulation of aerospace vehicles. This approach has served me well over 30 years. I hope that you will also benefit from it by the diligent study of the following chapters.

The second chapter, “Mathematical Concepts in Modeling,” lays the foundation through classical mechanics, a branch of physics. The axioms of mechanics and the principle of material indifference provide the sure footing for the modeling tasks.

With the hypothesis that points and frames are sufficient to model dynamic prob­lems, I build a nomenclature that is self-defining. For instance, the displacement of missile M from the tracking radar R is modeled by the displacement vector smr of the two points, whereas the angular velocity of body frame В with respect to the Earth E is given by the angular velocity vector u>BE. You will encounter other symbols that use points and frames, like linear velocity, angular momentum, moment of inertia, etc.

I permit only physical variables that are invariant under time-dependent coordi­nate transformations, that is, true tensor concepts. A construct like a radius vector has no place in our toolbox. Coordinate systems are abstract entities relating the components of a vector to Euclidean space. They have measure and direction, but no common origin. With these provisos we build our models with Cartesian tensors, as physical concepts, independent of coordinate systems.

With these tools we assail geometrical problems, like the near collision of two airplanes, both flying along straight lines; the miss distance of a missile impacting a plane; the imaging of an object on a focal plane array; and others. Problems at the end of the chapter invite you to practice your skills.

The third chapter, “Frames and Coordinate Systems,” distinguishes carefully between the two concepts. Frames are models of physical objects consisting of mutually fixed points, but coordinate systems have no physical reality. They are, as already characterized, mathematical abstracts. We make use of the nice properties of the transformation matrices between Cartesian coordinate systems. They are orthogonal, and therefore their inverse is the transpose. As the direction cosine matrix, they play an important part in flight mechanics.

No engineering discipline other than flight mechanics has to deal with so many coordinate systems. We will work with most of them: heliocentric, inertial, Earth, geographic, body, wind, and flight-path coordinate systems. We distinguish be­tween round rotating Earth and flat Earth. In Chapter 10,1 shall also introduce the oblate Earth and the geodetic coordinate system.

This chapter wraps up the modeling of geometrical problems. Do not under­estimate their importance. In a typical aerospace simulation you may find that one-third to one-half of the effort is expended to get the geometry right. The next chapter leads us to the kinematics of flight vehicles.

The fourth chapter, “Kinematics of Translation and Rotation,” introduces time and models the motions of vehicles without consideration of forces. We describe the translation of bodies by the displacement vector and their attitude by the ro­tation tensor. Their time derivatives are linear and angular velocities. It is here that I introduce the rotational time derivative, both for vectors and tensors. As already emphasized before, the rotational time derivative enables us to model flight dynamics by equations that are invariant under time-dependent coordinate transformations.

To shift reference frames, from inertial to Earth for instance, Euler’s transforma­tion is introduced. It is the generalization of the familiar form, shown in Eq. (1.1). Many derivations rely on it, particularly the formulation of the translational and attitude equations of motion. Shifting from the inertial to the Earth frame incurs such apparent forces as the Coriolis and centrifugal forces.

Finally in this chapter we solve the fundamental kinematic problem of flight dynamics, namely, given the body rates of the vehicle, determine the attitude angles. We take three approaches. The Euler method integrates the Euler angles directly with the penalty of singularities in the differential equations. Avoiding this disadvantage, the direction cosine and quaternion methods both solve linear differential equations. They are the preferred approach today because their higher computational load is no detraction any longer.

The fifth chapter, “Translational Dynamics,” introduces Newton’s second law for modeling the translational dynamics of aerospace vehicles. It is, together with Chapter 6, the heart of flight dynamics. Starting with the linear momentum, I formulate Newton’s second law first for particles and then for rigid bodies. The earlier teaser on the invariancy of Newton’s law will be fully developed. With Euler’s transformation I derive the Coriolis and Grubin transformations for shifts in reference frames and reference points, respectively. You will also get the first taste of simulations from the derivation of the translational equations for three-, five-, and six-degree-of-freedom (DoF) models.

The sixth chapter, “Attitude Dynamics,” formulates the attitude equations of motions based on Euler’s law. Conventional wisdom says that the attitude equations are a consequence of Newton’s law, but I will give evidence that Leonhard Euler developed them independently.

This chapter will challenge your mechanistic mind more than the rest of the book. I introduce the moment of inertia tensor with its axial and cross product of inertia. The moment of inertia ellipsoid gives a geometrical picture of the principal axes. As the linear momentum is at the center of Newton’s law, so is the angular momentum the heartbeat of Euler’s law. I start with particles and then expand the angular momentum to rigid bodies and eventually to clustered bodies. Euler’s law states that the inertial time rate of change of the angular momentum equals the externally applied moments. Again, we use the rotational time derivative to present Euler’s equation in tensor form, invariant under time-dependent coordinate transformations.

Now we are in a position to formulate the equations of motion of an aerospace vehicle and of a conventional spinning top. Of course, our emphasis is on free flight and on the significance of the c. m. of the vehicle. If the c. m. is used as reference point, Euler’s equation simplifies greatly and becomes dynamically uncoupled from the translational equation. With l as the angular momentum and m the externally applied moment, we can formulate Euler’s equation and combine it with Newton’s Eq. (1.2) for the fundamental equations of flight dynamics:

D’p = f, D’l — m (1.3)

All modeling in flight dynamics begins with these equations. They are the backbone of six-DoF simulations.

The ultimate challenge is the formulation of the dynamics of clustered bodies. With the theorems and proofs you should be able to derive the equations of motion of a shuttle releasing a satellite, the swiveling nozzle of a missile, or an aircraft with rotating propellers.

Finally, I will introduce you to the mysterious world of gyrodynamics. The unexpected response of gyroscopes, their precession and nutation modes can easily be explained by Euler’s law. With the energy theorem we derive two integrals of motion, the conservation of energy and angular momentum, which are pivotal for satellite dynamics.

The seventh chapter, “Perturbation Equations,” completes the assortment of modeling techniques. Although perturbation equations are rarely used for full – up simulations, they are important for stability investigations and control system design. Even here I emphasize the invariant formulation of perturbations, which leads to component perturbations and the general perturbation equations of flight vehicles for unsteady reference flight.

The perturbations of aerodynamic forces and moments are given close atten­tion. Taking advantage of the configurational symmetry of airplanes and missiles, vanishing derivatives of the Taylor series are sifted out and techniques presented for including higher-order derivatives.

As applications, we derive the roll, pitch, and yaw transfer functions for the autopilot designs of Chapter 10. More sophisticated examples are the perturbation equations of aircraft during pull-up, and of missiles executing high g maneuvers. These are illustrations of perturbation equations of unsteady reference flight, in­cluding nonlinear aerodynamic coupling effects.

Part 1 concludes here. It is a comprehensive treatment of Newtonian dynamics, sufficient for any modeling task in flight dynamics. The physical nature of the phenomena is emphasized by the invariant tensor formulation. Yet eventually, we have to feed our computers with instructions and numbers. That practical step is the subject of Part 2.