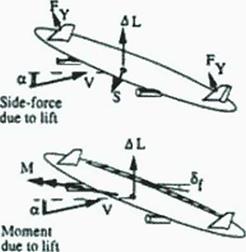
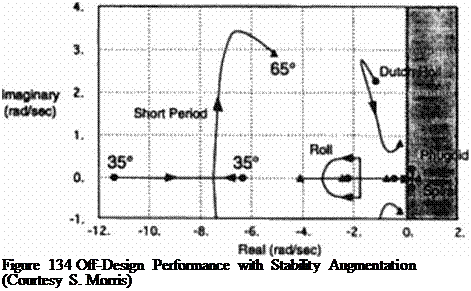
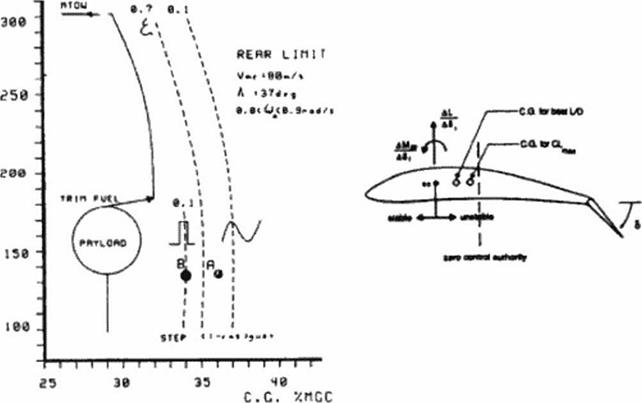
Economy
The aerodynamic and structural benefits of the oblique flying wing translate directly into better aircraft operating economy.
The oblique flying wing was directly compared with conventional supersonic and subsonic transports based on operating economy for a range of missions with specified performance and environmental constraints. All aircraft were evaluated with the same analysis routines and to the same level of structural, aerodynamic and propulsion technology comparable of that achieved by the new generation of subsonic transports. In terms of direct operating costs, oblique flying wings with more than 400 passengers were superior to conventional wing-body configurations over the entire Mach 0.8 to Mach 2.0 operating range The improvement was smaller than the uncertainty of the analysis at Mach 0.8. but more than a factor of two at supersonic speeds up to Mach 2.0. Unlike conventional delta wing transports it will be possible to design oblique flying wings for payloads up to 600 passengers and ranges up to 12000 km (6700nm) while satisfying current economic, performance and environmental requirements.
Table 6 compares a 400 passenger OFW and a 747*400.
|
OFW |
В 747-400 |
|
|
Cruise speed |
M 1.6 |
M 0.85 |
|
Range |
9000 km |
10300 km |
|
Geometry: |
||
|
Wing Area |
1316 |
511 |
|
cabin 1 x w (m) |
39.2 x 7.5 |
57×6.1 |
|
total 1 x w (m) |
120 x 14.5 |
69×60 |
|
Weights |
||
|
OE (kg) |
127000 |
180000 |
|
MTO(kg) |
30700 |
385000 |
|
SLS Thrust (kN) |
4×230 |
4×250 |
|
Price (1994) |
285 MS |
140 MS |
|
Production (scat. km. year) |
3.0 x 109 |
1.8 x 109 |
|
Est. Total Operating costs |
9 Set / pax. nm |
9 Set /pax. nm |
|
Table 6 Comparison of an OFW with a 747-400 |
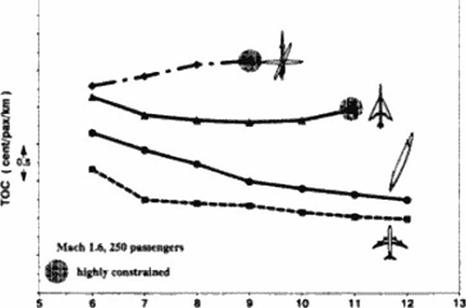
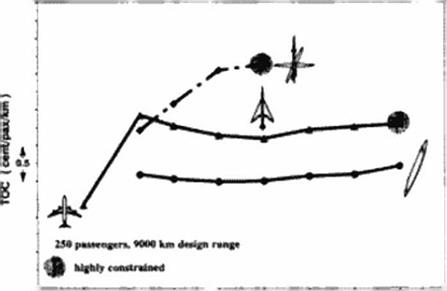
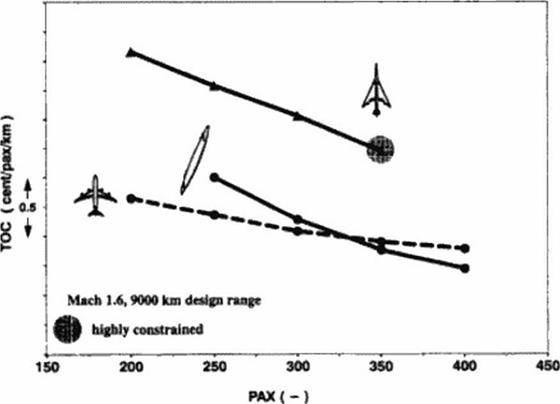
Figure 137 to Figure 139 compare the total operating cost of optimized oblique flying wings with other optimized aircraft configurations.
|
![]() Comparison of TOC’s as a Function of Range
Comparison of TOC’s as a Function of Range
|
|
Figure 139 Comparison of TOC’s as a Function of Size |
A cknowiedgcmtn is
The author would like to thank all his cotlegues at Stanford. NASA Ames and Daimler-Benz Aerospace Airbus who contributed to this project, especially Herbcn Sadowski for his work on the layout and the drawings and Dr. Steve Morris for his contributions to the stability and control part of this paper.
19.9 Conclusion
This paper shows that the oblique flying wing is a technologically and economically feasible transport.