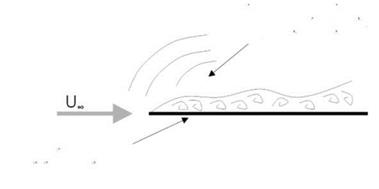
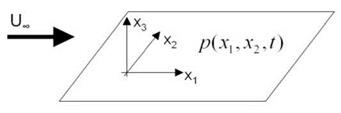
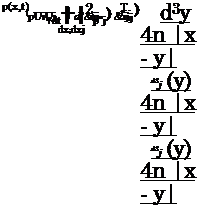With the term ‘Community noise’ we mean the far field noise generated at the flow side of a plate moving in a still fluid. Even though very difficult, several theoretical studies have been carried out with the aim of predicting the features of the pressure field radiated by a plane turbulent boundary layer. This topic was first investigated by Curle (1955) and Powell (1960a) using Lighthill’s analogy [Lighthill (1952)]. In the following, the integral formulations underlying those original approaches are briefly reviewed along with order of magnitude considerations to establish the importance of the radiative effects.
1.1 Integral formulations
The prediction of the propagation of acoustic waves in the far-field can be attained through an acoustic analogy approach and the search for a solution of the propagation equation derived therein. The reference theory is that of Lighthill (1952) that is based on the rearrangement of the Navier- Stokes equations to form an exact, inhomogeneous, wave equation, whose
 Acoustic pressure waves radiating in the
Acoustic pressure waves radiating in the
Community noise
fluctuations at the wa
 Acoustic pressure waves radiating in interior of the body
Acoustic pressure waves radiating in interior of the body
boundary of the body
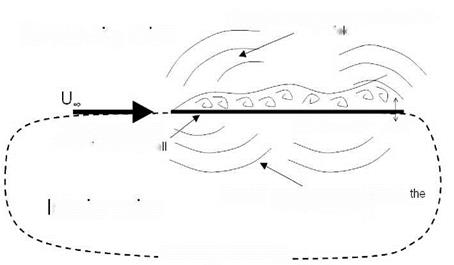
Figure 1. A scheme of the overall mechanisms generating sound waves from a turbulent boundary layer overflowing an elastic flat plate.
Acoustic pressure waves induced by the turbulent region (Curie s.
FWH. Howe s analogies)
Turbulence pressure fluctuations at the wall:
Statistical modeling of the
wavenumber-frequency spectra
Figure 2. A scheme of the theoretical problems faced in the present chapter.
source terms are significant in the neighborhood of vortical regions of the flow. As pointed out above, the sound is supposed to be a sufficiently small component of the whole motion that its effect on the main flow can be neglected. This hypothesis can be accepted in low Mach number (M) flows as well as in the absence of resonating systems and multiphase flows.
Detailed discussion about such an approach, elucidating also the applicability limits, are given in other chapters of the present book. Here we limit ourselves to recall the final form of Lighthill’s equation that can be written as:
 d^_c2y2p = d2Tjj dt2 Oxidxj
d^_c2y2p = d2Tjj dt2 Oxidxj
where Tij represents the Lighthill stress tensor that, neglecting the viscous terms, is denoted as follows:
 Tij = puiUj + (p – pc2)Sij
Tij = puiUj + (p – pc2)Sij
Here, c is the speed of sound, p and p are density and pressure perturbations, u the fluid velocity, x the spatial coordinate and t the time. This equation is valid within and without a source region. Where linear acoustics is valid, the acoustic pressure can be found from the relation p = c2p.
In the presence of solid boundaries, an integral solution of Eq. 1 is based on the introduction of a closed control surface S that may coincide with the surface of a moving body or mark a convenient interface between fluid regions of widely differing mean properties. When S coincides with the solid boundary, the solution of the equation is carried out by imposing suitable boundary conditions on it. The oldest strategy proposed to solve the propagation equation relies on the use of a proper Green’s function obtained as a solution of Eq. 1 when the source term is replaced by the impulse point source. The most general representation of this kind is due to Ffowcs Williams & Hawkings (1969), and is applicable to a control surface in arbitrary motion. This equation is obtained by deriving a wave type equation similar to that by Lighthill for a region made up of two subregions bounded by the control surface S. The region inside S contains fluid and/or solid boundaries, the region outside contains only fluid.
Without entering into the details, the integral form of the Ffowcs Williams and Hawkings equation can be obtained again making use of the free space Green’s function, leading to the outgoing wave solution. To the purpose of the present discussion, we can consider the case of a stationary control surface, leading the FWH equation to reduce to a simpler formula [see also
Howe (1998)] that was given previously by Curle (1955) and that we report in the following[23]:
As indicated by Howe (1998), Curle’s equation written for a rigid surface can be used to determine the order of magnitude of the sound generated by an acoustically compact body within a turbulent flow (e. g. a cylinder or an airfoil moving in an incompressible flow). This analysis applies also for non-compact bodies when turbulence interacts with compact structural elements, such as surface discontinuities, edges, corners.
The contribution from the quadrupole volume integral in Eq. 3 to the acoustic power П radiated in the far field, can be estimated to be
П <x v[24] M5
The quadrupole effect predicted by Eq. 4 is the same as in the absence of the body (it is the famous Lighthill’s ‘eight power’ law). On the other hand, at low M, the total power radiated by the dipole term (the first surface integral of equation 3) can be estimated to be:
thus exceeding the quadrupole power by a factor ~ 1/M[25] >> 1. The conclusion is that at low M the dipole term is largely dominant. This is the reason why surfaces with disconuities (such as sharp edges, steps, cavities) are much more noisy than smooth walls.
A different conclusion can be driven in the case of non-compact structures, that is, for objects whose size is not small compared to the acoustic wavelength, as is the case of an infinite rigid plate. Curle’s approach can again be used, and the presence of the infinite surface can be taken into account by introducing image vortices [Powell (1960b)]. Powell suggests
to use a Green’s function that is basically obtained by superimposing the free-space G with its image. In this way Powell shows that the pressure exerted on a plane boundary is the result of reflections of the quadrupole generators of the flow itself. In other words it is demonstrated that the surface integral is not a true dipole source but it represents the effect of image quadrupoles. Therefore, as concluded by Howe [Howe (1998)], the apparently strong contribution from the surface pressure dipoles actually reduces to a term of quadrupole strength, thus much less efficient, at low M, in terms of radiated pressure power. In the airframe noise context, if the effect of panel vibrations is not accounted for, it is reasonable to ignore the pure quadrupole radiation from the boundary layers, in comparison with that from edges and other inhomogeinities, such as wing trailing edge, flap side-edges, undercarriage gears and cavities. This is proven even for aircraft of large dimensions. As an example, the noise from the fuselage is expected to be more than 10dB below the level of the trailing edge noise.
However [Hubbard (1991)] the far field acoustic radiation due to panel vibrations might be a significant source of airframe noise in real (full-scale) aircraft. Furthermore [Howe (1998)] the presence of roughness breaks the Powell cancellation mechanism thus leading the dipole contribution to become relevant.
It should be pointed out that some recent numerical experiments [Hu, Morfey & Sandham (2002), Hu, Morfey & Sandham (2003) and Shariff & Wang (2005)] have focused on the role of the wall shear stress, rather than pressure, as sound source. They have shown that unsteady shear stresses can be an efficient sound source of dipole type that can be dominant at low Mach numbers and at very low frequencies.
We refer the reader to classical textbooks [such as Howe (1998)] and to the notes of the other authors included in this book, for further details on the integral approaches.













 6*
6*

 Acoustic pressure waves radiating in the
Acoustic pressure waves radiating in the