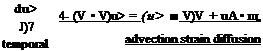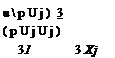Lifting-Line Blade Model
A very useful, but somewhat simplified, computational model of the aerodynamics of a rotor results from treating the blades as a series of 2-D blade elements, in the manner introduced in Chapter 3. If the velocity induced by the vortical wake of the blades can be calculated, then the induced AoA along the length of each blade can be found. The lift on the blade elements can then be determined and thus, by radial integration, the total blade lift. Lifting-line blade models that exploit this approach have found much use in helicopter rotor analyses and are to be found as the basis of nearly all forms of comprehensive rotor analysis (see Section 14.11). ,
To use the lifting-line model properly, though, the effects of the wake on the loading on the blade must be fully coupled to the circulation that is trailed (and shed) into the wake. This allows some 3-D effects to appear in the spanwise distribution of the blade loading, but because of small disturbance assumptions the method is not powerful enough to account completely for the strong 3-D flow effects found near the tip and root of the blade or near localized blade-vortex interactions, for instance. In principle, the models used in the helicopter field are similar to those used for fixed-wing analyses [see, for example, Houghton & Carpenter (1993)]. The lifting-line approach must be formulated carefully for use in rotating-wing applications, though, because the wake cannot be assumed to be planar, nor to extend downstream to infinity. Many different formulations can be found in the literature, with slight variations in assumptions in regard to the wake system. Although the basic principles are the same, the numerical formulation can vary substantially between implementations.
A generic formulation of the lifting-line problem will be described. For consistency with the results of Section 14.8, the blade is modeled as a vortex of strength Гb(y) that is “bound” to the aerodynamic center (1/4-chord). Then, using the Kutta-Joukowski theorem, the lift per unit span dL is given by
dL(y) = pV(у)Гb(y) dy = іpV(y)2cCi(y) dy
— ^pV(y)2Cia(y)ue{y)c dy, (14.52)
where ae is the “effective” AoA of that section and C/a is its lift curve slope. Often C/a is given the value 27r, being the lift curve slope of a 2-D thin airfoil in incompressible flow (see Section 14.8), but in practical applications the lift curve slope of the airfoil section at the appropriate combination of Mach number and Reynolds number can also be used. Assuming a thin airfoil and rearranging the terms gives
For a 2-D airfoil the bound vortex is an infinite line vortex and must have a strength that is defined on the basis of the downwash at a distance c/2 from the 1/4-chord, that is, by a condition of no flow penetration that is imposed at the 3/4-chord. This is consistent with the 2-D thin airfoil model of the problem that was described in the previous section. To extend this concept to three dimensions the blade is divided into N elements, as shown by Fig. 14.5, and a control point is placed at the 3/4-chord of each element. The normal velocity induced at the control point of panel і by the vorticity bound to element j can be written in terms of a matrix of influence coefficients, Ib, so that
Ubij rbj = Vat. (14.54)
The objective is to solve numerically for the distribution of bound circulation over the blade, Tb., which satisfies the no-flow penetration condition simultaneously at all of the control points on the blade. On the ith element of the blade,
N
Y, Vb + /»„].• J Г„,- = V № – фі) = Vae,, (14.55)
7 = 1
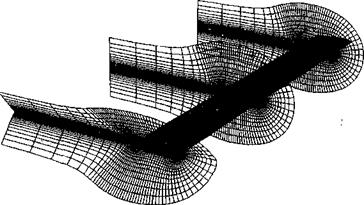
where Inw is the influence of the “near-wake” that must trail from the edges of the blade element. The near wake is usually modeled by a series of horseshoe vortices or vortex arcs
|
Figure 14.5 Lifting-line model representing the near wake trailed from a rotor blade. |
that trail downstream a finite distance, often to 15-30° of wake age, behind the blade. On the right-hand side of the equation, </>,■ contains the induced contributions from the remainder of the vortical wake (the “far wake”) and must exclude all of the induced effects from the parts of the wake that are defined as being part of the near wake. Applying this equation at all control points results in a linear set of simultaneous equations of the form
Ub + ІпіиІІГь) = {V (в – ф)}, (14.56)
from which the span wise loading (circulation) Г ъ can be obtained by standard numerical methods for solving systems of linear simultaneous equations. Both direct and iterative methods can be used, although direct methods are usually preferable because of their superior numerical behavior. In general, both Іь and Inw are matrices that are fully populated, although strongly diagonally dominant. Hence the structure of Іь and Inw cannot usually be exploited to simplify the numerical solution of Eq. 14.56.
From the resulting distribution of circulation along the blade span, the strengths of the vortices that trail from the edges of the blade elements (Fig. 14.5) can be calculated. These provide a boundary condition for the far vortex wake, which can be represented using a FVM, for instance. As mentioned previously, in many rotor wake modeling applications only the tip vortex is modeled, primarily for computational efficiency, but also because this vortex is the dominant flow structure in the rotor wake. This is because the high concentration of aerodynamic loading over the tip region of helicopter blades generally results in a powerful vortex rolling up and trailing from a point very close to the blade tip. It is often assumed for modeling purposes that all of the circulation outboard of the position of maximum bound circulation on the blade rolls up into this tip vortex. This is equivalent to assuming that the circulation about the tip vortex is the same as the maximum value of the bound circulation on the blade – see Question 14.6. This assumption can be used to define the initial strength (or circulation) of the vorticity in the far wake. The actual strength and initial location of the tip vortex may also be adjusted based on empirical data, if these are available. See Bhagwat & Leishman (2000a) for measurements of the relationship between the blade bound vorticity and the circulation in the trailed wake for a rotating blade.













 3 и dv
3 и dv
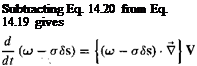 (14.20)
(14.20)