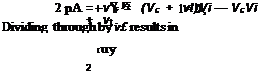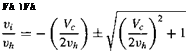Category Principles of Helicopter Aerodynamics Second Edition

The climb flow model cannot be used in a descent (where Vc <$C 0) because now Vc is directed upward and so the slipstream will be above the rotor. This will be the case whenever I Vc I is more than twice the average induced velocity at the disk. For cases where the descent velocity is in the range —2vh < Vc < 0, the velocity at any plane through the rotor slipstream can be either upward or downward. Under these circumstances, a more complicated recirculating (and usually more turbulent and aperiodic) flow pattern may exist at the rotor. Momentum theory. cannot be used here because no definitive control volume

Climb velocity ratio, V / vh

surrounding the rotor and its wake can be established – see discussion by Glauert (1935, p. 348). The same argument applies when using the blade element momentum theory (BEMT), which is discussed in Chapter 3. The more complicated operating state where —2Vh < Vc < 0 is discussed in Section 2.13.3.

The assumed flow model and control volume surrounding the descending rotor is shown in Fig. 2.19. To proceed, the assumption must be made that | Vc | > 2vh so that a well-defined slipstream will always exist above the rotor and encompassing the rotor disk. Far upstream (well below) the rotor, the magnitude of the velocity is the descent velocity, which is equal to I Vc. Notice that to avoid any ambiguity, it will be assumed that the velocity is measured as positive when directed in a downward direction. At the plane of the rotor, the velocity is I Vc| — Vi. In the far wake (above the rotor), the velocity is | Vc| — w.

By the conservation of mass, the fluid mass flow rate, m, through the rotor disk is

with the negative sign arising because the flow direction is now reversed (upward) compared to the climb case. In a steady descent, the velocity far upstream of (below) the rotor must be

(2.86)

which is a negative quantity. Therefore, the rotor is now extracting power from the airstream and this operating condition is known as the windmill state, for obvious reasons. More usually it is referred to as the windmill brake state because the rotor in this condition decreases or “brakes” the velocity of the flow – see Chapter 13. Using Eqs. 2.85 and 2.86 it is seen, again, that w = 2d,- . Note, however, that the net velocity in the slipstream is less than I Vc, and so from continuity considerations the wake boundary expands above the descending rotor disk. For the descending rotor

T = —mw — —pA(Vc + Vi)w = —2 pA(Vc + v;)i>; Therefore, we can write

(2.90)

Again, like the climb case, there are two possible solutions for /tih. One of these solutions produces values of vi/vh > 1, which violates the assumed flow model in this case. The only valid solution is

which is valid for Vc/vh < —2. Therefore, it is noted from Fig. 2.18 that as the descent velocity increases the induced velocity decreases and asymptotes smoothly to zero at high descent rates. The other solution to the quadratic, which is denoted by the broken line in Fig. 2.18, violates the assumed flow model and so is a nonphysical solution.

2.13.1 Axial Climb

Adequate climbing flight performance is an important operational consideration for a helicopter and sufficient power reserves must be available to ensure climbing per­formance is maintained over a wide range of gross weights and operational density al­titudes. Again, we can apply the three conservation laws to a control volume surround­ing the climbing rotor and its flow field, as shown in Fig. 2.17. As before, consider the problem to be quasi-1-D in that the flow properties will be assumed to vary only in the vertical direction over cross sectional planes parallel to the disk and at each cross section the flow properties are distributed uniformly. In contrast to the hover case where the climb velocity is identically zero, the relative velocity far upstream relative to the rotor will now be Vc. At the plane of the rotor, trie velocity will now be Vc + Vi, and the slipstream velocity

Figure 2.17 Flow model for momentum theory analysis of a rotor in axial climbing flight.

in the vena contracta is now Vc + w. By the conservation of mass, the mass flow rate is constant within the boundaries of the wake and so

m = JJ pV-dS = JJ^pV-dS, (2.71)

where dS is again the outward pointing normal from the control volume. Therefore, sub­stituting the values for this problem results in

m = pAoo(Vc + w) = pA(Vc + ы).

The application of the principle of conservation of momentum gives

T=jj p(V • dS)V – f f p(V ■ dS)V.

J J oo J Jo

Now, in a steady climb the velocity far upstream of the rotor is finite, so that both terms on the right-hand side of the above equation are nonzero. Therefore, in this case

T = m(Vc + w) — mVc = mw.

Notice that this is the same equation obtained for the rotor thrust in the hover case (Eq. 2.7). Because the work done by the climbing rotor is now T( VC + иг ), then

T(.vc + Vi) = II p(V-dS)V2- jjP(V-dSWi

= ^m(Vc + v})2 — jfflVc2 = lmu>( 2VC + u>). (2.75)

From these latter two equations, it is readily apparent that w = 2u,-, which is the same result as found for the hover case.

The relationship between the rotor thrust and the induced velocity at the rotor disk in hover is

and for the climbing rotor it has been shown from Eq. 2.74 that T = rirw — pA(Vc + Vi)w = 2 pA(Vc +

so that

which is a quadratic equation in v-Jvh. This equation has the solution

Although there are two possible solutions (one positive and one negative), гу /1v, must always be positive in the climb so as not to violate the assumed flow model. Therefore, the only valid solution becomes

(2.81)

The results from this analysis are shown in Fig. 2.18, which is presented in a form first suggested by Hafner (1947). The other root of the quadratic equation lies below the Vjvh axis and is physically invalid. It is apparent that as the climb velocity increases the induced velocity at the rotor decreases. This is called the normal working state of the rotor, with hover being the lower limit. The branch of the induced velocity curve denoted by the broken line gives a solution to Eq. 2.81 for negative values of Vc (i. e., a descent). However, just as the rotor begins to descend there can be two possible flow directions; this violates the assumed flow model and so this solution is also physically invalid. Yet the measurements follow closely this nonphysical root of the inflow equation, so in practice the momentum theory result can be assumed valid at least for low rates of descent.

The ratio T/P or the power loading has been previously defined as a rotor efficiency parameter. Helicopters and other rotorcraft are generally designed to hover with the lowest possible power required (and hence lowest fuel bum) for a given gross weight, that is, a high power loading with a large value of T/P is required. Helicopters spend a good proportion of their flight time in hover or low speed forward flight and the use of the hover condition as an initial design point is clear. However, as will be shown in Chapter 6, optimizing the rotor for maximum hovering efficiency can also have some trade-offs in terms of efficient high-speed forward flight performance.

Power loading is the ratio of the thrust produced to the power required to hover, that is,

This quantity should be as close as possible to the ideal value for best hovering efficiency. Because T oc (QR)2 but P oc (QR)2, maximizing the power loading requires a low tip speed (QR). On the basis of simple momentum theory considerations, the ratio P/T is given by

which, as also shown previously in Eq. 2.24, is related to the disk loading. Therefore, to maximize the power loading (that is to minimize the ratio P/T) the disk loading should be low (i. e., the disk area should be large for a given gross weight to give a low induced velocity and the tip speed should be low). Generally, the tip speed is set on the basis of various competing performance requirements for a given rotor size. As shown in Chapter 6, this may include autorotative requirements and rotor noise constraints.

When using the modified momentum theory, the ratio P/T is given by

P T. po

T V IpA + T ‘

Alternatively, we can write

which is a result that depends on the rotor solidity, a. Equation 2.67 can also be written in terms of the figure of merit, that is,

This means that the best rotor efficiency (maximum power loading) is obtained when the disk loading is a minimum and the figure of merit is a maximum.

A representative example of the measured CT/CP (which is proportional to power loading at a fixed tip speed) versus thrust is shown in Fig. 2.16 for several values of rotor solidity. By differentiating Eq. 2.67 with respect to CT, it is easy to show that for a rotor with rectangular blades the operating Cp to give the lowest ratio of T/P is

which clearly depends on both the profile and induced effects. Substituting this value into Ea. 2.46, for example, shows that this condition is equivalent to rotor operations at a figure of merit of 2/3к = 0.667к. Using this result, the disk loading for maximum power loading will be at

and for design purposes solving for the rotor radius would determine its optimum value for a given helicopter gross weight, tip speed, and density altitude. However, it is apparent that the conditions for the most efficient operation of the rotor are relatively insensitive to the operating state in that the Ст/Ср (or the T/P) curves in Fig. 2.16 are fairly flat over the normal range of operational thrust coefficients. Therefore, there is some latitude in selecting the rotor radius, which as mentioned previously, may be constrained because of other (nonaerodynamic) factors. See also the discussion in Section 6.4.1.

It will be seen from Eq. 2.46 that the solidity, a, appears in the expression for figure of merit, FM. For a rotor with rectangular blades, the solidity represents the ratio of the lifting area of the blades to the area of the rotor, that is,

blade area Ab NbcR NbC 2 61)

disk area А к R2 ж R

If FM is plotted for rotors with different values of a, the behavior is typified by Fig. 2.13. The data have been taken from the classic experiments of Knight & Hefner (1937), for which the thrust and power were measured for rotors with different numbers of blades. While the number of blades also affects rotor performance (see Section 3.3.10) there are no experiments that have examined solidity effects independently of blade number. Results predicted by means of the modified momentum theory are also shown in Fig. 2.13. From the measurements at zero thrust it was deduced that = 0.011, and к was estimated to be 1.25 and independent of the number of blades. While this value of к is perhaps on the high side for a modem helicopter rotor, it must be recognized that these measurements were made with untwisted blades and so, as will be shown in Chapter 3, this will produce higher induced flow near the tip and, therefore, the rotor is less efficient with a higher value of к.

From the results shown in Fig. 2.13 it will be noted that higher values of FM are obtained with the lowest possible solidity at the same design Cj (i. e., same aircraft gross weight or disk loading). This is hardly an unexpected result from Eq. 2.46 (all other terms such as к being assumed constant) and simply means that the viscous drag on the rotor is being minimized by reducing the net blade area. However, the minimization of rotor solidity, o, must be done with extreme caution. This is because reducing blade area must always result in a higher AoA of the blade sections (and higher lift coefficients) to obtain the same values of Cj and disk loading. Therefore, the lowest allowable value of a must ultimately be limited by the onset of blade stall. This effect is well shown by the results in Fig. 2.13 for the lowest solidity of 0.042, where a progressive departure occurs from the theoretical predictions for Cj > 0.004. For a full-scale rotor this would occur at higher values of Cj because of the higher values of maximum lift found at the higher Reynolds numbers on the blades – see Section 7.9.

An alternative format that emphasizes the local lift loading on the blades is to plot the figure of merit versus blade-loading coefficient, Cj/o. Notice that the blade-loading coefficient can be written as

Cj T / A T

a ~ pA(Q, R2) Аь) ~ pAb(QR)2 ’

2 / Fundamentals of Rotor Aerodynamics

where A* is the area of the blades. These results are shown in Fig. 2.14. Notice that reducing the value of a results in higher values of CT/a for the same operational value of 7. t oug. tg. .14 shows the rotor operates at higher values of FM with increased blade loading coefficient, the maximum value is limited by the occurrence of local flow separation on the blades and finally by blade stall. Typically, for a contemporary helicopter rotor, the maximum realizable value of blade loading coefficient without stall is about 0.12-0.14, but the influence of Reynolds number on blade stall must also be considered, especially with subscale rotors, which includes the measured data presented here.

The maximum attainable value of Cj jo will also depend on the distribution of local lift coefficients along the blade, which in turn depends on both the blade twist and the planform. As will be shown in Chapter 3, the local lift coefficients can be related to the blade loading by means of the blade element theory and so the blade twist and blade planform can be designed to delay the effects of stall to higher values of Cjjo. Nevertheless, it is clear that to maximize the figure of merit the blade sections must always operate close to their maximum lift coefficients (i. e., at the highest possible blade loading without the occurrence of blade stall). It can also be concluded that a rotor that uses airfoils with higher values of maximum-lift coefficient can be designed to have lower solidity. This has the benefits of a lower blade and hub weight, both of which are significant contributors to total helicopter weight. Consequently, there is considerable research emphasis in the helicopter industry to design airfoils with high values of maximum-lift coefficient (see Chapter 7).

Yet another form of presentation that emphasizes solidity effects is shown in Fig. 2.15. It is apparent that the figure of merit can be written in the alternative form

3/2

3 /2

In this case plotting FM versus CT /о causes the results for all rotors to coalesce essentially into a single performance curve. These results quickly confirm that the performance of a rotor is independent of the number of blades, but only if the performance is compared at the same value of solidity. While this is not strictly true because of secondary influences such as tip-loss effects and Reynolds number influences on Q0 (Nj, affects blade chord for a given value of solidity), the results shown in Fig. 2.15 are sufficiently convincing.

The formation of a trailed vortex at the tip of each blade produces a high local inflow over the tip region and effectively reduces the lifting capability there. This physical effect is shown in Fig. 2.11 in terms of the thrust distribution over the blade when compared at the same collective pitch (not at the same thrust). This phenomenon is often referred to as a tip loss, in that it represents a loss in lift relative to the finite value of lift that would

otherwise be produced without the influence of any tip vortices in the flow (i. e., a 2-D assumption).

In performance or preliminary rotor design work, a simple tip-loss factor В can be used to account for this physical effect such that the product BR corresponds to an effective blade radius, Re < R. A tip loss essentially corresponds to a reduction in the rotor disk area by a factor B2, that is

Ae = nR2 = n(BR)2 = B2(jxR2) = B2A. (2.51)

By a simple extension of this concept, the effect of the root cut out (essentially the inner, nonaerodynamic portion of the blade with retention and pitch attachments) can be esti­mated. If ro is the nondimensional radius of the root cut-out, then the effective area of the hovering rotor for momentum theory purposes becomes

Ae = 7tB2R2 – TirlR2, (2.52)

or in terms of an area ratio

Ae tcB2R2 —nr^R2 2 2

~A= ttR2 =B ~Г°’

Therefore, it will be apparent that this loss effect will manifest as a higher effective disk loading (i. e., T j Ae instead of T/A) and an increase in the average induced velocity by a factor B~x for a given thrust, with a corresponding increase in induced power.

This is also the essence of Prandtl’s approach to modeling tip-loss effects, where an analogy was made between the helical vortex wake below the rotor and a system of parallel vortex sheets – see exposition by Glauert (1935). Prandtl showed that when accounting for the tip loss, the effective blade radius, Re, is given by

where Nb is the number of blades. For helicopter rotors А,- is typically less than 0.07; thus kj will be small and the preceding equation can be simplified to

A more general tip-loss equation is sometimes used where

and where the inflow ratio is A = (Vc + u,)/ £25 and Vc is the climb velocity. For hovering flight with the assumption of uniform inflow it has already been shown that

(2.57)

so that the tip-loss factor is approximated by

A graph of this result is shown in Fig. 2.12, where the factor В is shown to decrease with decreasing number of blades and also with increasing rotor thrust. The former effect results from blade-to-blade interference, whereas the latter effect has its origin in the spacing of the vortex sheets below the rotor (helical pitch of the wake). In practice, values of В for helicopter rotors are found to range from about 0.95 to 0.98, depending on the number of blades.

Gessow & Myers (1952) suggest an empirical tip-loss factor based on blade geometry alone where

(2.59)

and where c is the tip chord, although it would seem that this result is not general enough to deal with other than rectangular blade tips. Sissingh (1939) has proposed the alternative geometric expression

where Co is the root chord of the main blade and г,- is the blade taper ratio (i. e., the ratio of the tip chord to the root chord). The need to determine В by one of these equations can, however, be avoided if a more general numerical approach to solving for tip-loss effects is used (see Section 3.2.4).

It is often necessary to estimate values for the induced power factor, к, and the average profile drag coefficients of the blades, Cdo, from rotor thrust and power measure­ments. These values are then used in various performance estimations. This can be done given measurements of CT and C pin sufficient quality and quantity, these normally being made by testing an isolated rotor (i. e., without the airframe) on a hover tower when the rotor is high enough off the ground to be free of ground interference effects. It has been shown that the result in Eq. 2.43 gives a good representation of hover performance, that is,

Worked Example 2 Posted by admin in Principles of Helicopter Aerodynamics Second Edition on February 4, 2016 A tilt-rotor aircraft has a gross weight of 45,000 lb (20,400 kg). The rotor di­ameter is 38 ft (11.58 m). On the basis of the momentum theory, estimate the power required for the aircraft to hover at sea level on a standard day where the density of air is 0.002378 slugs ft-3 or 1.225 kg m~3. Assume that the figure of merit of the rotors is 0.75 and transmission losses amount to 5%. A tilt-rotor has two rotors, which are each assumed to carry half of the total aircraft weight, that is, T = 22,500 lb. For each of the rotors, the disk area is, A = 7t(38/2)2 = 1134.12 ft2. The induced velocity in the plane of the rotor is The ideal power per rotor will be Tvt — 22,500 x 64.56 = 1,452,600 lb ft s-1. This result is converted into horsepower (hp) by dividing by 550 to give 2,641 hp per rotor. Remember that the figure of merit accounts for the aerodynamic efficiency of the rotors. Therefore, the actual power required per rotor to overcome induced and profile losses will be 2,641/0.75 = 3,521.5 hp, followed by multiplying the result by two to account for both rotors, that is, 2 x 3,521 = 7,043 hp. Transmission losses account for another 5%, so that the total power required to hover is 1.05 x 7, 043 = 7,395 hp. The problem can also be worked in SI units. In this case, Г = 10,200×9.81 = 100,062N. The disk area is, A = тг(11.58/2)2 = 105.32 m2. The induced velocity in the plane of the rotor is The ideal power per rotor will be Tvi — 100,062 x 19.69 = 1,970.2 kW. The actual power required per rotor to overcome induced and profile losses will be 1, 970.2/0.75 = 2,626.9 kW followed by multiplying the result by two to account for both rotors, that is, 5,253.8 kW. Transmission losses mean that the total power required to hover will be 5,515.7 kW. 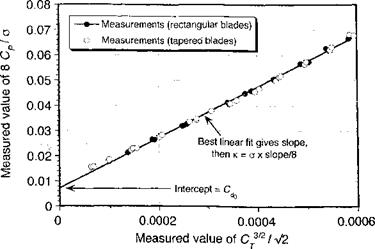Figure 2.10 Method used to determine the induced power factor and average profile drag coefficient from rotor thrust and power measurements. Data source: Althoff & Noonan (1990).   Worked Example 1 Posted by admin in Principles of Helicopter Aerodynamics Second Edition on February 4, 2016 In Chapter 1, the primitive helicopter built by Paul Cornu has been described. Each rotor of his machine was approximately 19.7 ft in diameter and the machine had a net gross weight (with pilot) of about 575 lb. Cornu claimed from experiments that 13 hp was required for the rotors to lift this weight. Use momentum theory to verify the power requirements for flight free of the ground. Assuming each rotor lifted half of the total aircraft weight, then the momentum theory gives a result for net minimum possible power (or ideal power) required to drive both rotors using 0 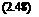2((W/2)W ideal_4 -ДрА )’ where the total take-off weight W — 575 lb and where each rotor had a swept disk area, A = 304 ft2. Assuming sea level air density, this gives the ideal shaft power (in horsepower) required to drive both rotors of Cornu’s machine as Therefore, an installed power of at least 14.7 hp would be required for free flight, but only if the rotors were aerodynamically 100% efficient and there were no transmission losses. Realistically, with the primitive types of rotors used by Cornu, we could expect the aerodynamic efficiency of the rotors to be no more than 50% (a figure of merit of 0.5) and so leading to a power required of about 30 hp. Remember that Cornu also used an inefficient belt and pulley system to drive the rotors from an engine that produced only 24 hp. Therefore, taking into account the aerodynamic efficiency of the rotors and with a conservative estimate of transmission losses, for Cornu to hover his machine free of the ground the installed power required would need to have been about 40 hp. Using an engine with a power output of only 24 hp it is highly unlikely that Paul Cornu’s machine ever flew freely in sustained flight, even when accounting for the benefits of ground effect (see Section 5.8) and discounting the losses in efficiency that would be encountered with the slippage of the belt transmission. Figure of Merit Posted by admin in Principles of Helicopter Aerodynamics Second Edition on February 4, 2016 There are several difficulties in defining an efficiency factor for a helicopter rotor because many parameters are involved, such as disk area, solidity, blade aspect ratio, airfoil section characteristics, and tip speed. The power loading parameter discussed previously is one measure of rotor efficiency because a helicopter of a given weight should be designed to hover with the minimum power requirements; that is, the ratio T/P should be made as large as possible. However, the power loading is a dimensional quantity and so a standard nondimensional measure of hovering thrust efficiency called the figure of merit has been’ adopted. This quantity is calculated using the simple momentum theory as a reference. The ideas of a figure of merit were first introduced by Renard (1903) and Glauert (1935), but it was introduced in its present form during the 1940s by Richard H. Prewitt of Kellett Aircraft. The figure of merit is equivalent to a static thrust efficiency and defined as the ratio of the ideal power required to hover to the actual power required, that is, Ideal power required to hover FM = ——– f^—— ———————— <1- (2.44) Actual power required to hover The ideal power is given by the simple momentum result in Eq. 2.34. For the ideal case, the figure of merit must always be unity because the momentum theory assumes no viscous losses; hence the ideal power is entirely induced in origin. In reality, viscous effects manifest as both induced and profile contributions, and these are always present in actual power measurements. Therefore, for a real rotor the figure of merit must always be less than unity. The figure of merit or FM can be used as a gauge as to how efficient a given hovering rotor is in terms of generating thrust for a given power. However, to qualify this, it should only be used as a comparative measure between two rotors when the rotors are also compared at the same disk loading, a point made again later. The figure of merit can also be written as where the measured value of power coefficient, C/>meas, will include both induced effects and all of the other “nonideal” physical effects that have their origin from viscosity. 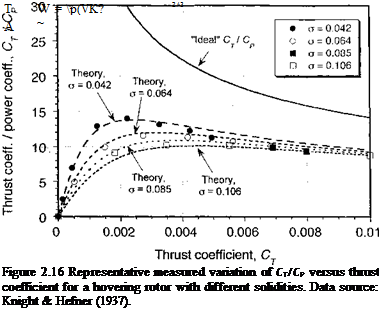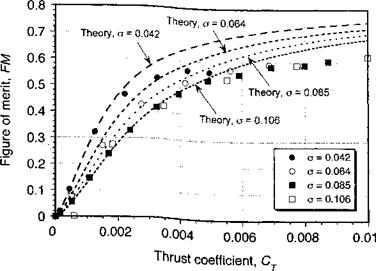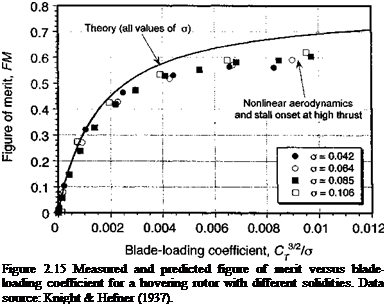A representative plot of measured figure of merit versus rotor thrust is shown in Fig. 2.8. It will be apparent that the FM reaches a maximum and then remains constant or drops off slightly. This is because of the higher profile drag coefficients (> C^) obtained at higher rotor thrust and higher blade section AoA. For some rotors, especially those with less efficient airfoils, the curve can exhibit a peak in FM, followed by either a progressive or abrupt decrease thereafter. Therefore, the FM behavior in the high thrust range will, to some extent, be a function of airfoil shape and airfoil stall type (i. e., gradual or abrupt – see Section 7.9). In practice, FM values between 0.7 and 0.8 represent a good hovering performance for a helicopter rotor. State-of-the-art rotors may have figures of merit approaching 0.82 (see Fig. 6.2), although this probably represents the upper limit for a helicopter rotor with conventional technology. 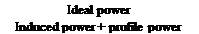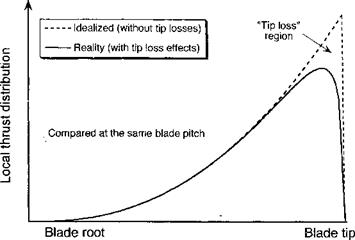Using the modified form of the momentum theory with the nonideal approximation for the power, the figure of merit can be written as c3/2 kC3t/2 oCb V2 8 (2.46) with the results being shown in Fig. 2.8. Notice that at low operating thrusts the figure of merit is small. This is because in Eq. 2.46 the profile drag term in the denominator is large compared to the numerator. As the value of CT increases, however, the importance of the profile power term decreases relative to the induced term and FM increases. This continues until the induced power dominates the profile term and the figure of merit will begin to approach a value of 1/k, which is shown more clearly in Fig. 2.9. In practice, however, the profile drag contribution decreases this value somewhat. Therefore, the FM curve reaches a firm plateau region, which represents the maximum attainable FM of the rotor. In practice, at higher values of rotor thrust the profile drag (and power) increases quickly as the blade begin to stall, which will again cause a reduction in FM. It has been mentioned that to be meaningful the figure of merit must only be used as a gauge of rotor efficiency when two or more rotors are compared at the same disk loading. This is because increasing the disk loading, DL (= T/ A) will increase the induced power relative to the profile power, producing a higher figure of merit and a potentially misleading comparison between two different rotors. This can be seen if the figure of merit is written dimensionally as Therefore, it would be considered inappropriate to compare the values of the figure of merit of two rotors with substantially different disk loadings because the rotor with the higher disk loading will generally always give the higher figure of merit, all other factors being equal (i. e., it would not be meaningful to compare the values of FM of a helicopter rotor with its relatively low disk loading to a tilt-rotor with its much higher disk loading). Therefore, caution should always be exercised in the use of FM as a means of comparing the efficiency of different rotor systems. 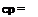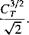Comparison of Theory with Measured Rotor Performance Posted by admin in Principles of Helicopter Aerodynamics Second Edition on February 4, 2016 In terms of coefficients it is apparent that the ideal power according to the simple momentum theory can be written as /ґ 0^74 Figure 2.7 shows a comparison of the simple momentum theory with thrust and power measurements made for a hovering rotor using Eq. 2.37. Notice that the momentum theory underpredicts the actual power required, but the predicted trend that Cp ос Сът/2 is essentially correct. These differences between the momentum theory and experiment occur because viscous effects (i. e., nonideal effects) have been totally neglected so far. 2.4 Nonideal Effects on Rotor Performance kC3t/2 V2 ’ In hovering flight the induced power predicted by the simple momentum theory can be approximately described by an empirical modification to the momentum result in Eq. 2.34, namely where к is called an induced power correction factor or just an induced power factor. This coefficient is derived from rotor measurements (see Section 2.9) or flight tests and it encom­passes a number of nonideal, but physical effects, such as nonuniform inflow, tip losses, wake swirl, less than ideal wake contraction, finite number of blades, and so on. For prelim­inary design, most helicopter manufacturers use their own measurements and experience to estimate values of к, a typical average value being about 1.15. Values of к can also be computed directly using more advanced blade element methods (see Chapters 3 and 10), where the effects of the actual flight condition can be more accurately represented. This is particularly important for high-speed forward flight, where the increasing nonuniformity of the inflow from reverse flow on the retreating blade must be accounted for. Wake swirl effects serve to reduce the net change of the fluid momentum in the vertical direction and they will decrease the rotor thrust for a given shaft torque (power supplied) or will increase the rotor power required to produce a given thrust. Johnson (1980) shows that as a result of wake swirl the induced power is increased by a factor [1-f Ct ln(Cy /2) – b CV/2]-1; this is less than 1% at the values of Су typically found on helicopters and can be neglected as a contributor to rotor power requirements. However, see also the discussion of wake swirl in Section 3.3.6. Proper estimates for the profile power consumed by the rotor requires a knowledge of the drag coefficients of the airfoils that make up the rotor blades; that is, a strip or blade element analysis is required. The airfoil drag coefficient will be a function of both Reynolds number, Re, and Mach number, M, which obviously vary along the span of the blade. A result for the profile power, Pq, can be obtained from an element-by-element analysis of sectional drag forces (i. e., the blade element method – see Chapter 3) and by radially integrating the sectional drag force along the length of the blade using P0 = QNb f Dydy, (2.39) Jo where Nb is the number of blades and D is the drag force per unit span at a section on the blade at a distance у from the rotational axis. The drag force can be expressed convention­ally as D = f>U2cCa = ір(ад2сС,, (2.40) where c is the blade chord.. If the section profile drag coefficient, Q, is assumed to be constant (= Cdf) and independent oiRe and M (which is not an unrealistic first assumption), and the blade is not tapered in planform (i. e., a rectangular blade), then the profile power integrates out to be P0 = – pNbtfcC^R4. Converting to a standard power coefficient by dividing through by pA(QR)3 gives (Nbcr _ 1 7TR)Cdo 8 The grouping NbcR/A (or Nbc/nR) is known as the rotor solidity, which is the ratio of blade area to rotor disk area and is represented by the symbol a. Typical values of a for a helicopter rotor range between 0.05 and 0.12, and much use of this solidity parameter is made throughout this book. 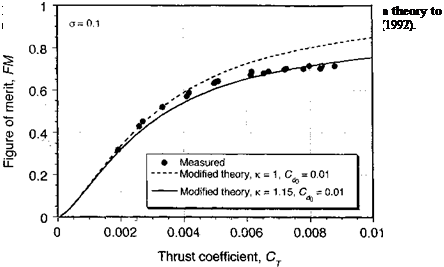Armed with these estimates of the induced and profile power losses, it is possible to recalculate the rotor power requirements by using the modified momentum theory result that r3/2 r Cp = CPi + CPo = K-±- + (2.43) These alternative results are also shown in Fig. 2.7, as denoted by the “modified theory,” which has been calculated by assuming Cd0 = 0.01. In the first case, it has been assumed that к = 1.0 (ideal induced losses), and in the second case, к = 1.15 (nonideal losses). The value of cr for this particular rotor is 0.1. Notice the need to account for nonideal induced losses to give agreement with the measured data. The overall level of correlation thus obtained gives considerable confidence in the modified momentum theory approach for basic rotor performance studies, at least in hover. « Previous 1 … 32 33 34 35 36 37 Next » Tweet Copyright © 2024 Helicopters & Aircrafts - Everything about aircrafts and helicopters. News and events in aviation worldwide. Civil, transportation, military helicopters and airplanes.