Effects of the Fuselage on Rotor Performance
Betzina & Shinoda (1982), Smith & Betzina (1986), Brand et al. (1986, 1989, 1990), and Leishman & Bi (1990a, 1990b, 1994a, b) have conducted wind tunnel tests to investigate aerodynamic interactions using subscale rotors and relatively simple bodies of revolution. Most studies have concluded that the rotor performance was to some extent affected by the presence of the body, but that the aerodynamic characteristics of the body were highly modified by the presence of the rotor and its wake. Such tests on fairly generic fuselage configurations (easy to define geometrically) can help the analyst to better isolate the specific aerodynamic phenomena that allow for fundamental understanding. For example, Fig. 11.2 shows an example of a subscale rotor with a geometrically simplified airframe being tested in a wind tunnel, in this case with a body of revolution for the fuselage and a simple T-tail empennage. There was no tail rotor in this case. These types of geometrically simplified setups gives the analyst the ability to carefully study the flow physics of specific aerodynamic phenomena with greater confidence than could be done with more representative helicopter airframe configurations. The results also give the analyst the best opportunity to precisely define the geometry of the problem to validate computational flow studies. This will help to improve confidence levels in comprehensive flow models that predict the detailed viscous flows about actual helicopter airframes.
|
Figure 11.2 A subscale helicopter rotor with a geometrically simplified airframe (body and T-tail) geometry being tested in a wind tunnel. |
|
Figure 11.3 The figure of merit of the rotor will be affected by the presence of an airframe. Data source: Bagai & Leishman (1992). Analysis: Crouse & Leishman (1992). |
Perhaps surprisingly, it has been found that the introduction of a body into the flow field near the rotor can give a beneficial reduction in rotor power requirements for a given thrust, but only when operating in hover and in forward flight at low advance ratios. For example, Fig. 11.3 shows the figure of merit of a rotor for a range of thrust coefficients in hover. Results are shown with and without a body.[43] As the rotor thrust increases, the presence of the body produces an increase in the rotor figure of merit; the increase shown (about 5% at Ст /cr = 0.10) is clearly significant. There is also a download on the airframe induced by the rotor (which governs the net vertical force on the rotor-airframe combination), an effect that is discussed in Section 11.2.2. The most obvious reason for the change in rotor performance is the body’s effect on the induced inflow through the rotor disk; the body reduces the inflow through the disk in the regions directly above itself and changes the effective angles of attack on the blade elements. This, in turn, affects the lift distribution over the blades, which becomes more heavily biased toward stations further inboard for a given rotor thrust. While the blade airloads are also unsteady, the effect of the body has the same effect as increasing the average value of the effective blade twist (in a more ideal way). It is apparent then that this particular interaction is actually beneficial and, in this case at least, gives the rotor increased hovering efficiency.
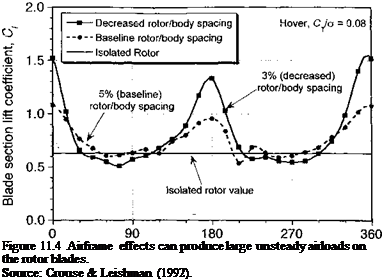
To expound on this point, Fig. 11.4 shows a plot of the computed time history of the lift coefficient at an inboard section of the blade in the region directly above the body surface. Clearly the mean value of lift is increased by the body, which is a direct result of the decrease in induced inflow at this blade station by the influence of the body. Furthermore, notice that, compared to values for the isolated rotor, the lift is now time-varying, with a 2/rev unsteady component. Because, in this case, a four-bladed rotor was used, the net effect of this interaction will be an 8/rev aerodynamic excitation at the rotor. As the blades pass over the rear of the fuselage (at jr = 0°) notice that there is a stronger effect than when the blades pass over the front of the fuselage (at 1fr = 180°). This is expected based on the slightly larger clearances between the blades and the nose of the body. The results also
 |
Blade azimuth, – deg.
show that decreasing the spacing between the rotor and the body amplifies the unsteady lift. (There is also a reciprocal effect on the airframe airloads – see Fig. 11.15.) This is an example of why decreasing the rotor-airframe spacing on a helicopter generally increases vibratory airloads and why, if the spacing becomes too small, vibration problems will result that are difficult to solve (especially for helicopters using rotors with higher disk loadings) unless rotor-airframe spacing is ultimately increased again.
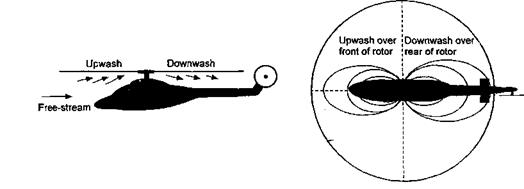
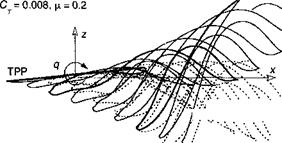
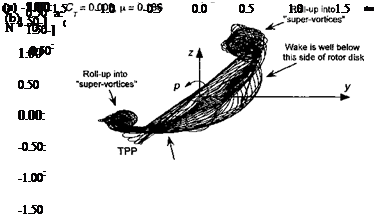
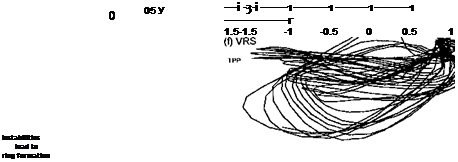
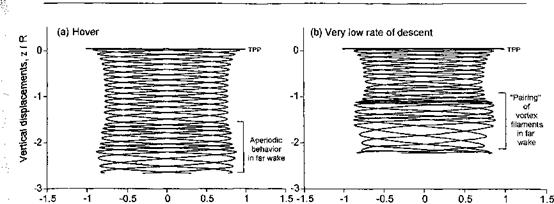
Similar types of interactions also occur in forward flight. However, the relative position of the rotor wake to the body is important here, and the wake position becomes a function of rotor thrust and advance ratio (see Section 10.4.1). There are also self-induced effects on the rotor wake that are produced by wake distortions induced by the airframe surfaces. As forward speed increases, the rotor wake quickly skews behind the rotor disk and the wake interactions between the rotor and the body become somewhat weaker. Yet, there are also other complicating aerodynamic factors that occur in forward flight. One is that the fuselage produces flow field perturbations in the rotor plane as forward speed builds – see Fig. 11.5. This effect, however, becomes significant only at relatively high forward speeds
|
Figure 11.5 Fuselage effects in forward flight will cause an upwash perturbation over the front of the rotor and a downwash over the rear of the disk. |
Cp/o Cp/o
 |
(say for jJL > 0.3) but it can make a difference to the blade airloads and rotor performance. However, the unsteady effects from blade passage and induced pressures associated with the convection of the discrete wake vortices (see Section 11.2.3) remain important at all advance ratios, and these effects may even increase in intensity at higher forward flight sneeds as rotor thrust increases to meet Drooulsive reauirements.
і 1 1
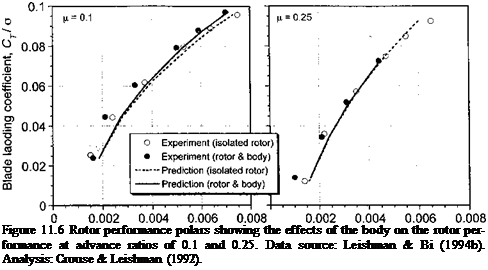
Figure 11.6 shows an example of the rotor performance polars in forward flight at advance ratios of fi = 0.10 and /z = 0.25. At the relatively low advance ratio of /z = 0.10 there are notable differences between the performance of the rotor with and without the body present. As expected, the changes become more apparent at higher rotor thrust values as the interactions between the rotor and the airframe strengthen. As the advance ratio is increased, however, the effects of the body on the rotor are progressively reduced. At an advance ratio of (i — 0.25 there are almost no differences between the rotor-body case and the isolated rotor. This is because the wake is now much further away from the fuselage, and there is a weaker body-induced wake distortion – see Figs. 11.7 and 10.10. At this condition the rotor and the body each behave more like they would in isolation, although not completely. At both advance ratios, the analysis [Crouse & Leishman (1992)] predicts the changes in the rotor power to within the bounds of experimental measurement uncertainty. See Section 11.2.3 for modeling requirements and the types of approaches.
|
(a) Low-speed forward flight (b) High-speed forward flight
Figure 11.7 As forward speed is increased the main rotor wake is skewed behind the rotor, (a) Low-speed flight, (b) High-speed flight. |
|
Figure 11.8 The effect of increasing advance ratio will initially be to decrease the significance of rotor-airframe interactional effects on rotor performance. Data source: Leishman & Bi (1994b). Analysis: Crouse & Leishman (1992). |
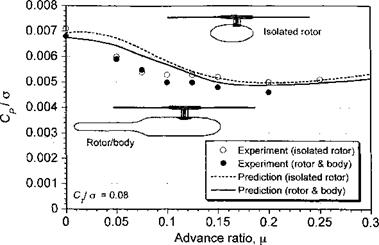
The net rotor power required for rotor operation at the same nominal thrust over a range of advance ratios is shown in Fig. 11.8. As expected, the greatest differences between the isolated rotor and the rotor-body combination are in low-speed flight; as advance ratio increases the differences decrease. It might be expected that at very high advance ratios (>0.4) some degree of interaction returns because the fuselage will produce larger flow disturbances in the rotor plane, as suggested by Fig. 11.5. This effect has been studied by Wilby et al. (1979), Ryan et al. (1988), Dehondt & Toulmay (1989), and Rand & Gessow (1989) using a potential flow methodology. This seems to give a good first order approximation to the perturbations in blade angles of attack caused by the fuselage. The interactional effects, however, are confined mostly to the regions near the rotor hub, which do not contribute as much to rotor lifting and propulsive capability. The effects, therefore, show up more in blade airloads and aeroelastic response and less in contributing to overall rotor performance.















 і/all oc tbp rvAOitiAnc /"vf tbp urobp filomantc гріotitra trv ‘V VU (40 411V/ ^WOltlVllO VI 411V/ W C4JVV – 111CU11V/1140 1. V/1C441 V V/ IV
і/all oc tbp rvAOitiAnc /"vf tbp urobp filomantc гріotitra trv ‘V VU (40 411V/ ^WOltlVllO VI 411V/ W C4JVV – 111CU11V/1140 1. V/1C441 V V/ IV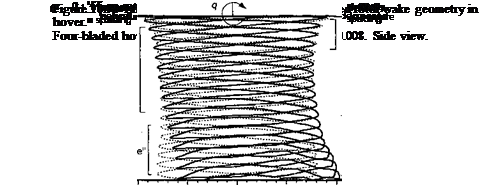
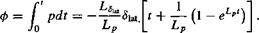 (10.131)
(10.131)




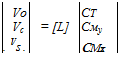 (10.123)
(10.123)
 (10.124)
(10.124)