Moving into the area of high-speed aerodynamics as applied to propellers, the definitions of the speed of sound and its associated critical Mach number and the effects of compressibility will now be considered.
The speed of sound varies with the ambient temperature and air density. Because air density is closely related to temperature, it can be ignore in the calculations. At sea – level where the International Standard Atmosphere (ISA) temperature is assumed to be +15 °C (288 K) the speed of sound as 661 knots and varies in proportion to the square root of the Absolute temperature. The speed reduces to 575 knots in the Stratosphere where the temperature is assumed to be at minus 56.5 °C (or 216.65 K). The speed of sound is also known as acoustic velocity, Mach number 1, or more simply as Mach 1, after Dr. Ernst Mach (1838-1916) the Austrian philosopher and physicist. Mach number is the ratio of aircraft speed to the speed of sound, or in this case the propeller tip speed to the speed of sound.
At subsonic speeds, below Mach 0.8, air acts as if it is incompressible and this assumption is fine until speeds greater than 300 knots and altitudes of 10,000 feet are considered and where the effects of compressibility and air density can no longer be ignored. The aircraft wings, or prop blades, cause compressibility as they move through the air sending pressure waves ahead of it, which travel at the speed of sound and cause the approaching air flow to separate and travel over and under the wings or prop blade surfaces. As the prop tips approach the speed of sound, the pressure waves have less time to move ahead of the blade and they eventually become stationary on the blade’s surface. This causes an increase in compressibility resulting in a serious loss in propeller efficiency, which in turn, reduces thrust and causes a rapid rise in blade drag, prop torque and especially noise.
Altitudes above 25,000 to 30,000 feet are the domain of jet propelled aircraft and not many propeller-powered aircraft are found there, due to the reduction in air density, air temperature and pressure. Propellers are unable to cope with the reduced air density at these high altitudes and at 40,000 feet the thrust produced by the propeller is reduced to around 25% of the sea-level value. How does the reduced air density at high altitudes affect the thrust produced by the prop? An inspection of the familiar lift formula below shows it can be applied to the propeller thrust:
Thrust (or lift) = CL%pV2S
Where CL = lift coefficient % = a constant p = air density V = prop RPM in FPS S = prop blade area
If the blades area (S) is assumed to be constant and the air density (p) is reduced at altitude, the lift coefficient (CL) and prop speed (V) are the two variables. The lift coefficient can be increased by increasing the blade pitch angle but this increase is offset by the prop speed decreasing. [Remember that coarse pitch produces lower RPM]. Therefore, with the lift coefficient, RPM2 and blade area all doing nothing to increase prop thrust, it follows the remaining factor of air density is the only remaining variable and because air density decreases with altitude, prop thrust must also decrease.
It is common knowledge air temperature decreases along with air density as altitude increases. Not only is the prop’s thrust decreasing with altitude but the speed of sound is also decreasing This has a detrimental affect on propeller performance The prop blades are working closer to the speed of sound at altitude than they do at sea-level due to the difference in air temperature. This can be shown by calculating the tip Mach number (Mt) for a given aircraft’s prop at sea – level (s/l) and for example 20,000 feet from the formula:
Tip Mach number = V. tip/speed of sound
Where: Prop tip speed (V. tip = 870 FPS S/l speed of sound = 1100 FPS 20,000 feet speed of sound = 1040 FPS
Mt at s/l (15 °C) = 870/1100 = Mach 0.79 Mt at 20,000 feet (-25 °c) = 870/1040 = Mach 0.83
In the above figures, the prop has a higher tip Mach number at altitude and it is therefore operating closer to the speed of sound with efficiency deteriorating. Closely associated to the speed of sound is the term critical Mach number. This is the speed at which the airflow over a body, or prop blade, reaches Mach 1.0, due to the blade’s curved upper surface, while the prop blade itself is actually moving at a speed below Mach 1.0 . It is the thickness/chord ratio that determines the critical Mach number of an airfoil, which increases with thinner prop
blades with a high aspect ratio and is therefore more important operationally than the speed of sound.
Incidentally, when the prop tip approaches the speed of sound, a condition occurs known as ‘cavitation’, caused by a near vacuum on the suction face of each prop blade near the tips, which again reduces efficiency.













 Negal
Negal




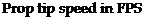 RPM x diameter
RPM x diameter


