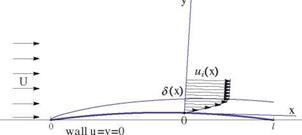
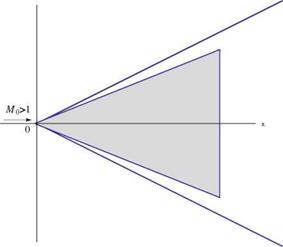
Numerical Method for the Solution of Boundary Layer Equations
A Cartesian mesh system is defined, with constant steps Ax and Ay and indices i and j in the x – and y-directions, respectively. This is an initial/boundary value problem. Before the obstacle, a uniform flow is specified ui, j = U, vi, j = 0, j = 1, jx. The pressure gradient or source term is specified from the inviscid flow solution. The continuity equation is used to solve for v and the momentum equation for u. Consider the x-momentum equation:
![]() _du _du dui d2 u
_du _du dui d2 u
dx + p – y = >m~du + >‘dy
where u and v are evaluated from previous iteration (for initial guess, extrapolate from previous line). Two boundary conditions are specified for u, i. e.
![]() У1 = 0, ui,1 = 0, yjx = h, ui, jx = U, i = 2,…
У1 = 0, ui,1 = 0, yjx = h, ui, jx = U, i = 2,…
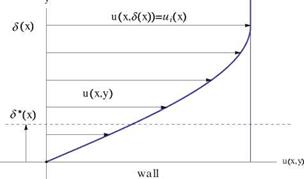
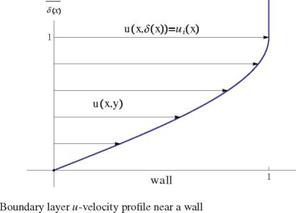
h is the ordinate of the upper boundary, h > 5(l), large enough to include the boundary layer.
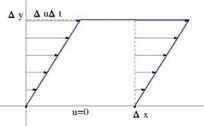
Central finite differences are used for the first and second partial derivatives of u in y
![]()
![]()
![]()
![]()
and i
A tridiagonal solver is used to obtain ui, j for line i = 2,…
Note that, as long as ui, j > 0, the tridiagonal matrix is diagonally dominant, which insures stability with respect to round-off errors.
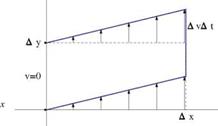
Consider next the continuity equation to solve for v. One boundary condition is specified
![]() У1 = 0, v;,1 = 0, i = 2,…
У1 = 0, v;,1 = 0, i = 2,…
![]()
![]()
![]()
The following scheme is used
![]() i = 2,…, j = 1,…, jx — 1
i = 2,…, j = 1,…, jx — 1
This equation is marched upward along the vertical line, solving for vi, j+1.
The process is repeated, i. e. one iterates on u and v on line i until convergence (3 or 4 iterations). Then, one marches to the next line i + 1. The domain is swept once in the flow direction.











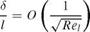

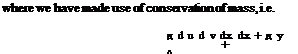

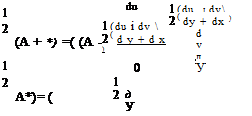
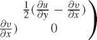


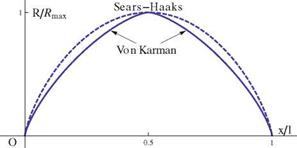
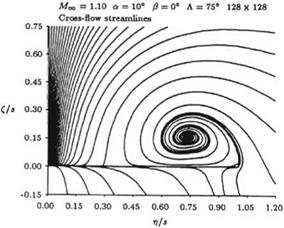
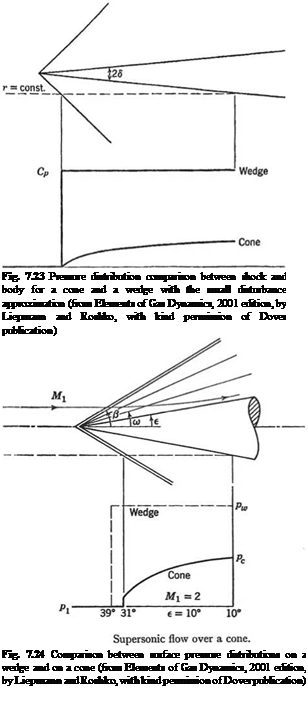
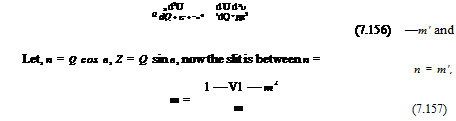
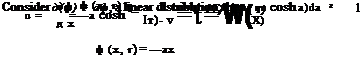
 (cot8 ( 2
(cot8 ( 2