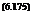Conical Flows
7.9.1 Method of Taylor and Maccoll
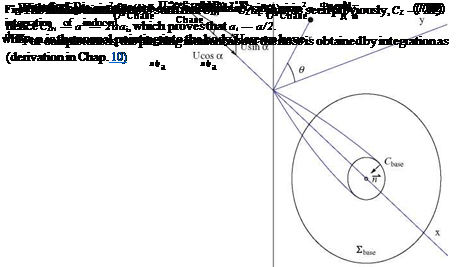
Consider supersonic flow over a cone at zero incidence, with a conical shock attached to the tip of the cone. The shock is of uniform strength and the entropy jump across the shock is also uniform, hence the flow between the shock and the cone is isentropic and irrotational. Unlike the two-dimensional wedge case, the corresponding governing equations are complicated. In the following, numerical integration due to Taylor and Maccoll [30] will be discussed.
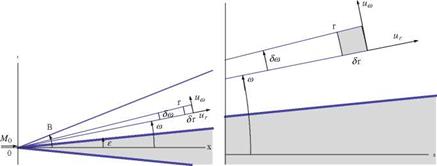
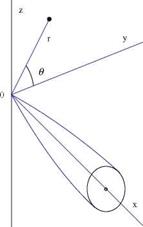
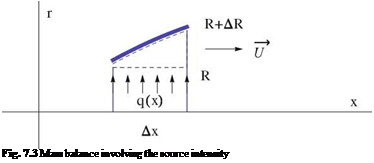
Assuming that all the fluid properties are constant on cones with common vertex at the tip of the cone, and using spherical coordinates, the equation of continuity, the definition of vorticity and Bernoulli’s law are given below (Shapiro [31]). Conservation of mass from control volume analysis, Fig.7.22, reads
|
|
|
|
Since д/дг = 0, then д/дш = d/dш and the above equation becomes
![]() dum dp
dum dp
2pur + рию cot ш + p + ию = 0
d ш d ш
Irrotationality, Fig. 7.22, yields
|
|
||
|
|||
|
|||
![]()
![]()

The integration of the above equation was first done by Busemann, using a graphical construction in the hodograph plane. Later, Taylor and Maccoll [30] used a straightforward numerical integration.
(i)
Begin with
(ii) Integrate the nonlinear O. D.E. stepwise, using small steps in a, by replacing the derivatives by finite differences.
(iii) After finding ur/ Vmax for each value of a, calculate ua/Vmax using the irrotationality condition in discrete form.
(iv) The final step is to find the shock angle в and the free stream velocity U/ Vmax. For each value of a during the integration, the downstream Mach number M of a shock with an angle в — a and turning angle в are compared with the value of M obtained from the integration process. If the two numbers agree, the limit of integration has been reached.
The incoming Mach number M0 can be found from the shock tables. The shock relations together with the isentropic relations for the conical flow region provide all the necessary information.
As in the wedge case, one may construct a shock polar in the hodograph plane.
For each value of M0 there exists a maximum value of the cone semi-angle e for which there is a solution to the conical flow equations, and vice-versa, for each value of e, there is a minimum M0. Also, for a given M0 and for e < emax, there are two solutions, with strong and weak shocks. Since the flow behind the strong shock is always subsonic, which cannot be conical, the strong shock is not possible and should be eliminated. On the other hand, the weak shock solution is possible with finite cones in supersonic flow because cutting off the downstream part of the cone cannot affect the upstream flow.
Notice for equal cone and wedge angles, the surface pressure rise and shock angle are smaller for cones due to the three dimensional effects.











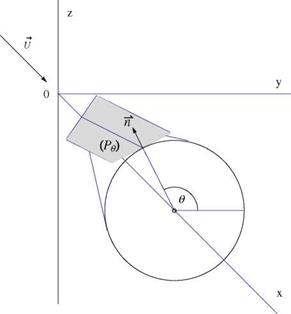
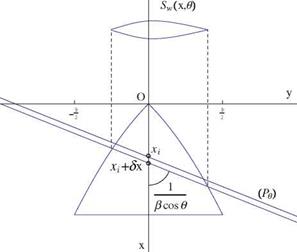
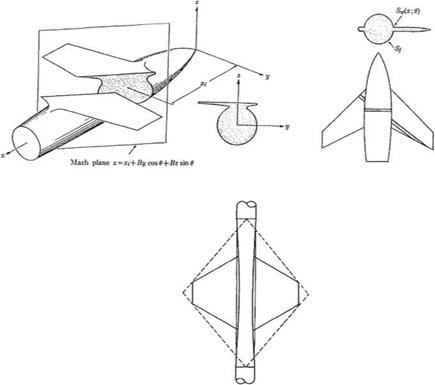
 Minimum wave drag (for non lifting configuration) can be achieved by choosing Se (x) to be an optimum shape, i. e. the Sears-Haaks body. Thus the fuselage will be indented in the region of the wing.
Minimum wave drag (for non lifting configuration) can be achieved by choosing Se (x) to be an optimum shape, i. e. the Sears-Haaks body. Thus the fuselage will be indented in the region of the wing.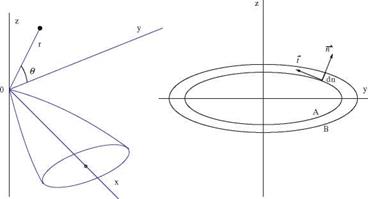
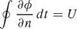
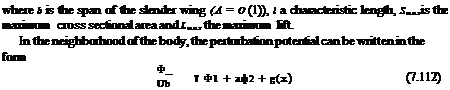

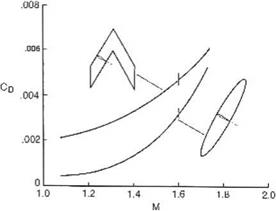
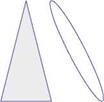 Fig. 7.12 Drag due to lift: oblique elliptic wing and delta wing, M = 2
Fig. 7.12 Drag due to lift: oblique elliptic wing and delta wing, M = 2
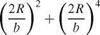 Lw+b Lw
Lw+b Lw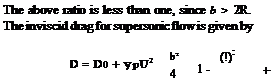
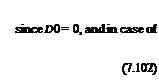 The drag for subsonic flow reduces to induced drag R = 0, it becomes
The drag for subsonic flow reduces to induced drag R = 0, it becomes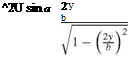

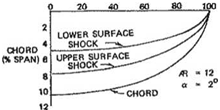
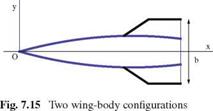
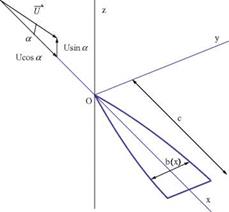 Fig. 7.10 Low aspect ratio flat wing
Fig. 7.10 Low aspect ratio flat wing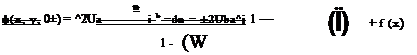



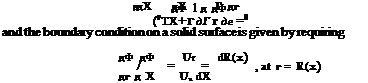

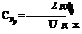
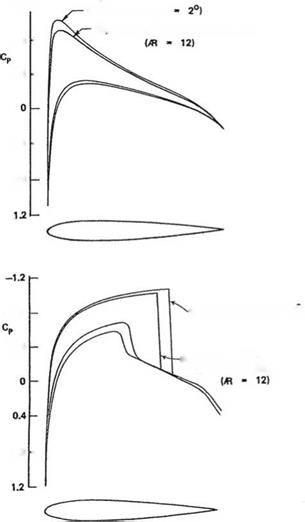 2D SOLUTION (a
2D SOLUTION (a