Forces
The momentum theorem applied to a large control volume surrounding the wing and bounded by a surface £, yields the resulting force
F =-J (pV(V. n) + pn) d£ (6.13)
When the flow on the wing does not present singularities, such as a leading edge singularity, thanks to an adapted leading edge, the surface £ can be shrunk to the surface of the wing and the force reduces to
F =- pndA (6.14)
wing
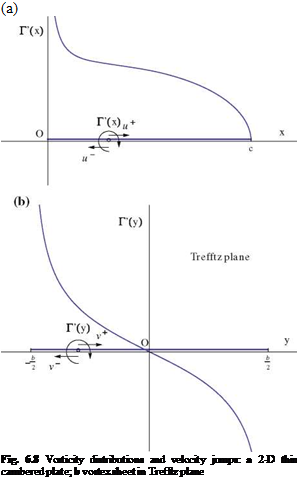
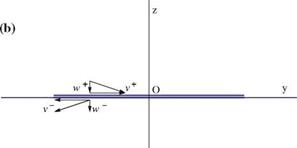
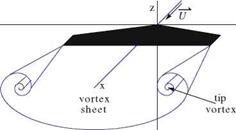
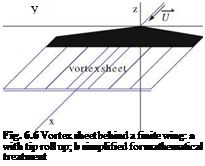
However, the flow is in general singular along the leading edge of the wing, even in supersonic flow if the leading edge sweep is large enough, and the integration of pressure will miss the contribution due to that singularity, the suction force. Hence it is best to integrate on a surface that stands away from the wing. Typically one uses a cylinder of large radius R, denoted £R, and two planes perpendicular to the x-axis to close the control volume, one far upstream where the flow is undisturbed, £0, and one far downstream treated as the Trefftz plane, £T, Fig. 6.11. The control volume surface is £ = £r U £0 U £T. On £0, the flow is uniform and V = {U, 0, 0}. Perturbations may be present on £R due to shock waves crossing the boundary in supersonic flow regime and u, v, w have jumps along the shock trace. In £T, far downstream, the flow will be perturbed in the vicinity of the vortex sheet. The pressure has returned to pro, i. e. u = 0, but v, w are different from zero, with v being discontinuous at the sheet and v, w tending to zero far from the x-axis.
The expression for F can be simplified by introducing a small perturbation assumption and expanding the dependent variables p, V and p with respect to a small parameter є, where є can represent relative thickness, camber or incidence, as
p = Pro + єр1 (x, y, z) + є2р2(х, y, z) +–
V = U i + єV1 + e2V2 + ■■■ =
{U + ємл(х, y, z) + є2иа(х, y, z) +—— ;
єvl(x, y, z) + є2г02(х, y, z) +— ; .
єwl(x, y, z) + €2w2(x, y, z) +— }
. p = Pro + ProU2 {ep1(x, y, z) + Є2Р2(Х, y, z) +– )
It has been established by Viviand [1] that, to first order, the following relations hold
P1 = ~МГО u1
![]() Vx = Уф, V2 = V Ф2
Vx = Уф, V2 = V Ф2
pi = U1
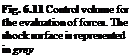 |
 |
which indicate that the flow remains irrotational at the first two orders, even in presence of shock waves (assumed to be weak). Rotation and entropy appear at third order. To find the forces, the expansions need to be carried to second order, but the result can be expressed in terms of the first order perturbations only.











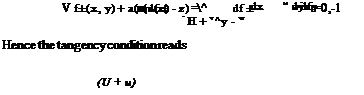
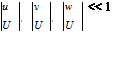

 (a)
(a)