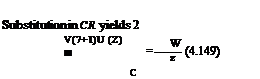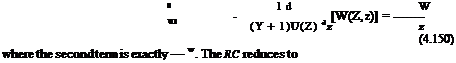The Transonic Small Disturbance Equation
The unsteady, transonic small disturbance equation (TSD) in Cartesian coordinates is given by
![]() (5.54)
(5.54)
![]()
![]()
where
K is the transonic similarity parameter. For an airfoil of chord length c, traveling with speed U with an oscillating frequency w, the reduced frequency is defined as
к = (5.56)
U
2
The perturbation potential in the above equation is scaled by є 3, where є is the small parameter representing the profile thickness, camber or incidence, while x, y
1
and t are scaled with c, с/є 3 and 1 /w, respectively.
2
For low reduced frequencies, when к = O(є3), the equation becomes
![]() д2ф д2ф д2ф
д2ф д2ф д2ф
2 p __ с
dt дх д x2 д у2
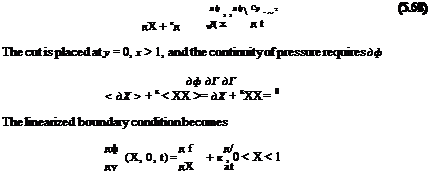 |
The pressure coefficient is
where the profile is given by у = є f (х, t).
The far field non-reflecting downstream boundary condition becomes
![]() дф дф
дф дф
дХ + k д =0
Notice, this condition is consistent with the treatment of the cut.
The shock jump condition for the unsteady TSD, low frequency approximation, is obtained from the conservation form of the equation [4]
and from the irrotationality condition д2ф/дхдy = д2ф/дудх
Here, we made use of < u2 >= 2u < u >, where U = (u1 + u2)/2, is the average of u across the shock. Also, nt/пх = —йхя/dt is the speed of the shock in the х-direction. With this, the shock equation becomes
2B (dt), < дф >> + (К — <Y + 1)M2 дф) < дф >2 + < д >2= 0
(5.65)
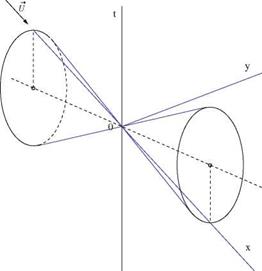
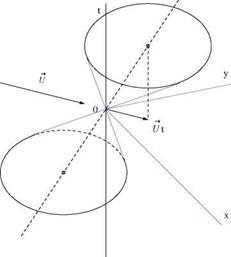
The equation is always of hyperbolic type. One family of characteristic surfaces through the origin comprises the plane t = 0 that corresponds to an infinite speed of propagation of the perturbations. The other family are planes that envelop a cone of equation
2 Bxt + Ct2 = (By)2 (5.66)
The cross section of the cone by a plane t = const is a parabola having the х-axis as axis of symmetry, Fig. 5.10. The origin is inside the parabola when M0 < 1, and outside when M0 > 1. The tangents to the parabola from the origin represent the characteristic lines of the steady flow.
Next, the sources of material of this section are summarized.
First, the linear theory for high frequency transonic flow is discussed by Landhal [5]. The more recent, nonlinear small disturbance theory is discussed by Cole and Cook [6]. The numerical treatment and numerical results can be found in the articles of Ballhaus and Lomax [7], Bailey and Ballhaus [4], Goorjian [8] and van der Vooren
 |
and Schippers [9]. Engquist and Majda covered the mathematics and numerics of absorbing boundary conditions in [3] and [10]. Applications of non-reflecting boundary conditions to unsteady transonic flow computations were reported by Kwak in Ref. [11]. Many others contributed to NASA codes for low frequency transonic flows and flutter analysis.











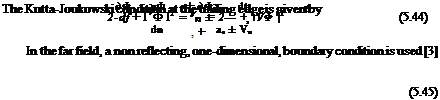
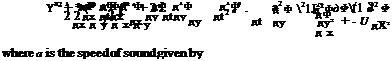

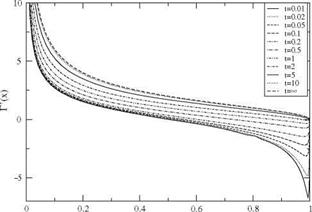
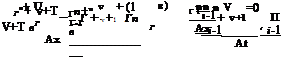
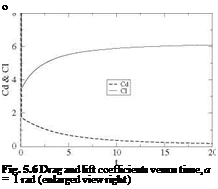
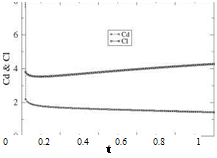
 finds Ci = 160.5 and Cd = 158.9. Then drag decreases monotonically to zero as steady-state is approached, whereas lift decreases then increases to its final value of n. If the term D’2 had been included, the result for drag would have been Cd (t) = Cl (t) since w(x, 0, t) = —Ua =—U and (xQ — x)da + d = 0. Enlarging the scale near t = 0 provides a better look at the early evolution of those coefficients, Fig. 5.6. One can see from the numerical results that, at the first time step, the suction force is not present, but with the second time step the suction force already cancels half of the drag.
finds Ci = 160.5 and Cd = 158.9. Then drag decreases monotonically to zero as steady-state is approached, whereas lift decreases then increases to its final value of n. If the term D’2 had been included, the result for drag would have been Cd (t) = Cl (t) since w(x, 0, t) = —Ua =—U and (xQ — x)da + d = 0. Enlarging the scale near t = 0 provides a better look at the early evolution of those coefficients, Fig. 5.6. One can see from the numerical results that, at the first time step, the suction force is not present, but with the second time step the suction force already cancels half of the drag.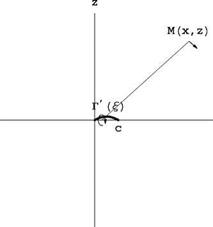 Fig. 5.3 Far field evaluation of potential
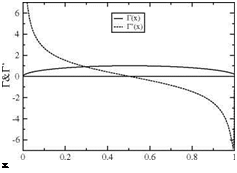
Fig. 5.3 Far field evaluation of potential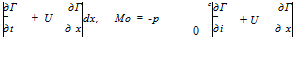
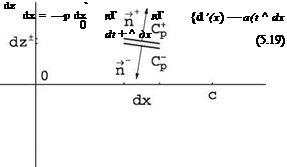
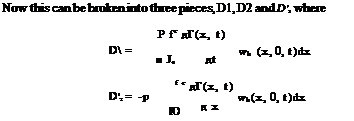


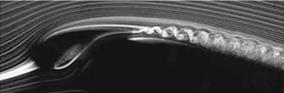
 Fig. 4.22 Problem 4.9.6: Shadowgraph of bullet at Mach = 1 (from https://en. wikipedia. org/wiki/File: Shockwave. jpg Author: Dpbsmith (Daniel P. B. Smith))
Fig. 4.22 Problem 4.9.6: Shadowgraph of bullet at Mach = 1 (from https://en. wikipedia. org/wiki/File: Shockwave. jpg Author: Dpbsmith (Daniel P. B. Smith))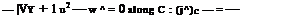
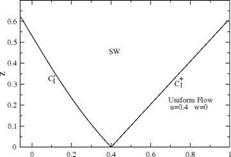 Fig. 4.21 Subdomain SW adjacent to uniform flow region
Fig. 4.21 Subdomain SW adjacent to uniform flow region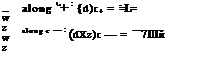
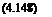 /zi(Z) (Y+1)U (Z)
/zi(Z) (Y+1)U (Z)