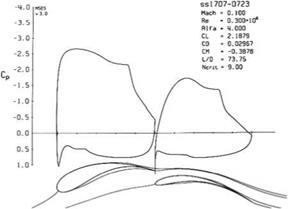
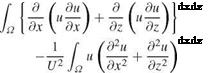Linearized Supersonic Flow
Let в — M2 – 1, when M0 > 1. The potential equation for linearized supersonic
flow is of hyperbolic type and models wave propagation. It is analogous to the wave equation that models the vibrations of a string. The PDE and boundary conditions read:
![]()
![]()
—0
ф(х, z) ^ 0, x2 + z2 ^ to, almost everywhere
The general solution of the PDE, the d’Alembert solution, is given by
ф(х, z) — F(x – ez) + G(x + ez) (4.23)
where F(ф) and G(Z) are arbitrary functions of a single argument. These unknown functions are uniquely determined by the boundary conditions. It is easy to verify
|
Fig. 4.4 D Alembert solution for the upper surface |
that such a solution satisfies the PDE with any functions F and G. The families of straight lines, £ = x – pz = const. and Z = x + pz = const. are the characteristic lines of the PDE. They represent, in this approximation, wave fronts of infinitesimal perturbations as well as shocks and expansion waves of finite strength. They have slopes dz/dx = ±1/p.
Consider a profile placed along the x-axis, 0 < x < c. The supersonic flow is from left to right. Upstream of the profile leading edge the flow is undisturbed. Perturbations will occur downstream of the two characteristics passing through the origin. Consider first the upper surface. The C+ characteristic through O and C+ through the trailing edge delimit a semi-infinite strip where the perturbation due to the profile affects the flow solution, see Fig.4.4.
The solution will be obtained once the expressions for F and G are found. In the undisturbed flow region, upstream of the C0+ characteristic, the solution for the perturbation potential is ф = const. = 0 (the potential is defined up to an arbitrary constant). In other words:
F(x – вz) + G(x + pz) = 0, Vx, z, z > 0, £ = x – pz < 0 (4.24)
which implies that F = G = 0. Furthermore, since G remains constant along the Z = x + pz = const., G = 0 in the semi-infinite strip 0 < £ = x — pz < c. The solution there reduces to ф(x, z) = F (x — pz). In order to apply the tangency condition, one needs to calculate the ш-component along the x-axis. It is
дф(x, z) , дф(x, 0+) , /,
= F (£)(—p) ^ =-pF'(x) = U(f +(x) – a) (4.25)
dz dz
The last equation can be readily integrated as an ODE to give
Finally, the constant is found by enforcing continuity of the potential at x = 0, hence the constant is zero. The above equation defines the functional form of F. Replacing x with £ extends the definition of ф from the axis to the semi-infinite strip as
ф(x, z) = – U (f + (x – вz) – a(x – вz) , z > 0, 0 < £ = x – вz < c (4.27)
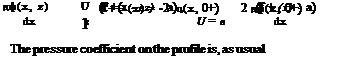 |
|
Note that, above the airfoil, the solution is only a function of £ = x – вz. It is also easy to see that the tangency condition for w(x, 0+) is satisfied. There remains to calculate the u-component on the profile and the pressure coefficient. The former is now obtained:
Proceeding in a similar way, one would find that, below the profile, the potential is ф(x, z) = G(x + pz) (i. e. F = 0 for z < 0, 0 < Z = x + вz < c) so that, upon satisfying the tangency condition w(x, 0-) = U(f -(x) – a), the perturbation potential is found to be
U
ф(x, z) = в (f (x + вz) – a(x + вz)), z < 0, 0 < Z = x + вz < c (4.30) The u-component of velocity on the profile is now
The expressions for C± (x) are known as Ackeret formulae.
Note that there was no reference to a Kutta-Joukowski condition, even when there is circulation and lift. Indeed, due to the wave character of supersonic flow, the
solution, hence the forces and moment on the profile, do not depend on the solution downstream of the trailing edge. It is interesting, however, to discuss the solution downstream of the profile. At the trailing edge the potential is discontinuous. Indeed, the solution in the two semi-infinite strips above and below the profile reads:
Г ф(х, z) = – Ц (f +(x ~ вz) – a(x – f3z)), z > 0, 0 < £ = x – f3z < c
ф(х, z) = Ц (f -(x + вz) – a(x + вz)), z < 0, 0 < Z = x + ez < c
(4.33)
At the trailing edge the jump of potential is < ф(с, 0) > = ф(с, 0+) – ф(с, 0-) = Г (с) = 2вас. The potential function for a lifting problem is multi-valued and a cut is introduced to regularize it. Although it could be any line £ > с, я > с, originating at the trailing edge, it is convenient to align the cut with the x-axis. The cut does not represent a physical surface, streamline or wall, therefore pressure and velocity are continuous across it. The continuity of pressure or u(x, z) is simply r'(x) =< u(x, 0) >= u(x, 0+) – u(x, 0-) = 0, x > с. This condition can be integrated along the x-axis from x = с to give < ф(x, 0) >= ф(x, 0+) – ф(x, 0-) = Г (с).
The same result can be obtained when the cut is an arbitrary line. Above the cut the solution is still of the form ф(x, z) = F(x – ez), whereas below the cut it is of the form ф(x, z) = G(x + вz). The condition along the cut is therefore
F (x) – G(x) = Г (с) (4.34)
The continuity of the ш-component leads to
дф(x, 0+) , дф(x, 0-)
= – вF (x) = = вG (x), ^ F (x) + G'(x) = 0 (4.35)
dz dz
This last ODE can be integrated to give
F (x) + G(x) = соті. = 0 (4.36)
where the constant is obtained for x = с. From these conditions the solution for F and G is obtained:
![]() F = сон8і. = Цсї G = wnsi. = – r2f)
F = сон8і. = Цсї G = wnsi. = – r2f)
The solution reads
ф(x, z) = Цвас, z > 0, с < £ = x – вz
ф(x, z) = —Цвас, z < 0, с < Z = x + вz
The flow field, downstream of the profile is the uniform, undisturbed flow V =
(U, 0).











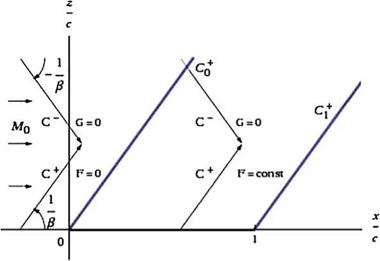

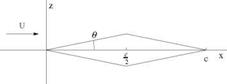
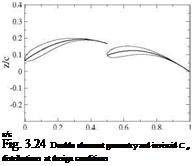
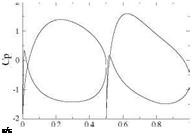
 Fig. 3.31 Problem 3.9.7: Flat plate with flap
Fig. 3.31 Problem 3.9.7: Flat plate with flap