Solution by the Time-Stepping Method
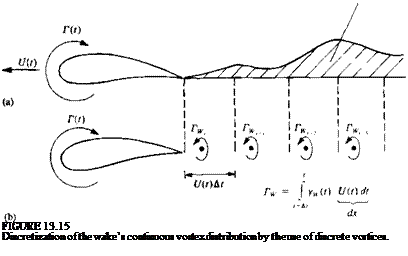
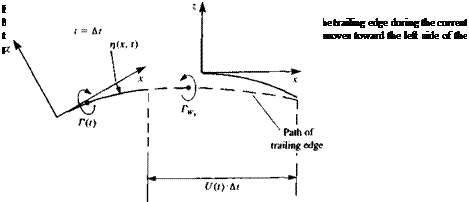
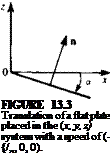
The above presentation of the thin-airfoil fluid dynamics is formulated as an initial-value problem. Typical initial conditions can be a steady-state motion or a start from rest. In the latter case there is no wake at t = 0 and the first wake element is formed at t = At. Consider the airfoil after the first time step At, as shown in Fig. 13.17a. The problem at this moment is to obtain the flow field details and to calculate the pressure difference across the airfoil, in the presence of one wake vortex—which represents the vorticity shed at the trailing edge since the initiation of the motion. To apply the results of the small-disturbance solutions of Sections 5.2-5.3, the airfoil’s camber and angle of attack are assumed to be small, rj/c «1, and the path curvature must be large (вс/и«1), so that the boundary conditions can be transferred to the z=0 plane. If the lifting thin airfoil is modeled by a chordwise vortex distribution y(x, t), then at the first time step this problem resembles exactly the model shown in Fig. 5.7, but with an additional wake vortex Гщ (Fig. 13.17a). The downwash induced by the airfoil bound circulation y(x, t) is
|
(a) |
|
Location of T. E. at t = 0 |
given by Eq. (5.38) (note that the boundary conditions are transferred to the 2 = 0 plane):
At any later time the downwash of the Nw discrete vortices of the wake (see Fig. 13.17b) on the airfoil can be summed numerically by using, for example, Eq. (11.1):
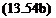 5Фіу, v _ v ^____________ X Xk_______
5Фіу, v _ v ^____________ X Xk_______
52 2n (x – xkf + (z-zkf
where к is the counter of the wake vortices. The downwash of the bound vortex distribution of Eq. (13.54a) must be equal to the right-hand side of the boundary condition in Eq. (13.50):
![]()
![]()
■ dn вх+ — dt
where the smaller terms were neglected. Substituting this approximate value of W(x, t) and dФв|dz from Eq. (13.54a) into the boundary condition (Eq.
|
0<*<c (13.56) |
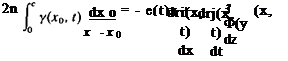 |
(13.50)) results in
which is the time-dependent equivalent of the steady-state boundary condition (Eq. (5.39)) and must hold for each point x on the airfoil’s chord. In addition, the Kutta condition is assumed to be valid for this flow (recall that вс/U « 1):
У(с,0 = 0 (13.57)
If the right-hand side of Eq. (13.56) is known then the solution for the vortex distribution is given in Section 5.3. In fact, all terms appearing in the right-hand side are known (will have numeric value) at any time t, excluding the latest wake vortex influence, which depends on the solution y(x, t). This difficulty can be overcome by assuming that the strength of the latest wake vortex is known, too, and adjusting for this assumption later.
The classical approach of Glauert, presented in Section 5.3, approximates y(x, t) by a chordwise trigonometric expansion at any time t. This requires the transformation of the equations into trigonometric variables as appear in Eq.
(5.45) :
![]() Q
Q
x = – (1 — cos d)
Based on this transformation, a solution similar to the vortex distribution of Eq. (5.48) is proposed for the time-dependent problem (at each frozen moment, t):
y(#, t) = 2U(t)[A0(t) ~ + C^ + 2 An(t) sin (nt?)l (13.59)
Substituting this proposed solution into the boundary condition (see details in Section 5.3, Eqs (5.49)-(5.53)) results in
= – Ло(0 + S An(t) cos (n#) (13.60)
Ut) n = l
 |
||
which is a trigonometric expansion of the momentary chordwise downwash. The coefficients An were found in Section 5.3 (Eqs. (5.51) and (5.52)) and are:
So at this point, if the momentary chordwise downwash W(де, t) is known then the momentary circulation distribution on the airfoil is known, too, from Eqs. (13.59), (13.61), and (13.62). However, as mentioned before, the strength of the latest vortex (Fig. 13.176) in the downwash term is unknown, but it can be calculated by using Kelvin’s condition (Eq. (13.51)). A simple iterative scheme to calculate the strength of this vortex is as follows: at a given time step assume that the strength of the latest vortex Гis known (0 or Г(ґ)/2 are reasonable initial assumptions). Then the total circulation (which must be zero for the converged solution) can be expressed as
,_i f for the ]
/(Г) = Г(/) + TW: + 2 TWk j =0 converged r (13.63) *-1 [_ solution J
where the first term is the airfoil’s circulation, the second term is the latest wake vortex, and the last term is the circulation of all the other wake vortices (which are known from the previous time steps). The circulation of the airfoil is obtained by using Eq. (5.58):
Г(0 = f y(x, t)dx= f y(0, t) ^ sin 0 dt?
Jo Jo 2
= 2U(t) f [a0(0 1 + C°^ + 2 A„(t)sin (ntf)l C-sin fldtf Jo L sin 17 n~ J 2
= (/(0ся[ло(0+^] (13.64)
The iterations for determining the strength of the latest vortex element (using a simple Newton-Raphson iteration) will have the form
(Ги’)у+і = (Гил)/ – 777^ (13.65)
/ l wjj
where j is the iteration counter and the derivative /'(Г) is approximated by
r(r) _№)>-/(Г)/-:]
‘ (^-(Г^
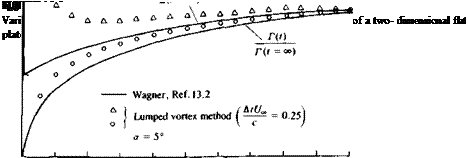
The solution of the momentary airfoil’s vortex distribution Г(г) can be summarized such that, first, at a given time step t, the downwash W(x, t) is calculated by Eq. (13.55). By assuming an initial vortex strength TWj for the most recently shed trailing edge vortex the wake influence is calculated via Eq. (13.546). So now the chordwise downwash W(jc, t) can be calculated at any point along the chord and, for example, can be evaluated at say 50 nodal points on the chordline. This allows the numerical computation of the coefficients An(t) and /(Г) (in Eqs. (13.61)-(13.63)). Then using Eq. (13.65) the next value of the latest wake vortex is obtained, and this short iterative process (beginning with the downwash calculation and ending with the value of
the chordwise vortex distribution) is repeated. This simple iteration scheme will usually converge within 3-5 iterations and this will conclude the solution of the vortex distribution for this time step.











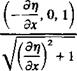 (13.44)
(13.44)
 (13.38)
(13.38)
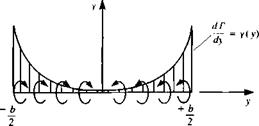 Spanwise circulation on a flat plate in a sinking motion.
Spanwise circulation on a flat plate in a sinking motion.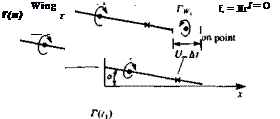

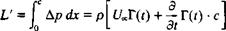 (13.36)
(13.36)
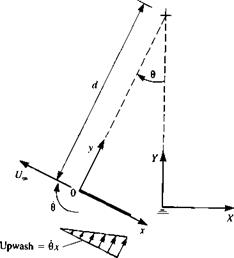 Motion of a flat plate along a circular arc with radius d.
Motion of a flat plate along a circular arc with radius d.
 (13.32)
(13.32)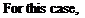 Similarly, the boundary condition for a statically spinning propeller blade can be established by rotating the blades at a rate ф about the x axis as shown in Fig. 13.6 (observe the definition of a in Fig. 13.6 for this example).
Similarly, the boundary condition for a statically spinning propeller blade can be established by rotating the blades at a rate ф about the x axis as shown in Fig. 13.6 (observe the definition of a in Fig. 13.6 for this example).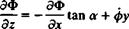 (13.33)
(13.33)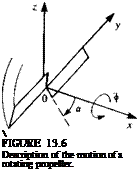
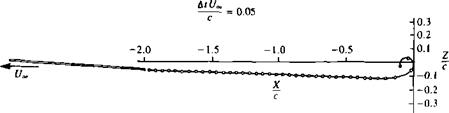
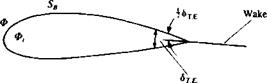 Possible assumption for wake shape near the trailing edge.
Possible assumption for wake shape near the trailing edge.