When treating time-dependent motions of bodies, the selection of the coordinate systems becomes very important. It is useful to describe the unsteady motion of the surface on which the “zero normal flow” boundary condition is applied in a body-fixed coordinate system (де, y, z), as shown for the example of a maneuvering wing in Fig. 13.1. The motion of the origin О of this coordinate system (x, y, z) is then prescribed in an inertial frame of reference (X, Y, Z) and is assumed to be known (as shown in Fig. 13.1). For simplicity, assume that at f = 0 the inertial frame (X, Y, Z) coincides with the frame (x, y, z). Then, at t > 0, the relative motion of the origin ( )0 of the body-fixed frame of reference is prescribed by its location Ro(f), and the instantaneous orientation of this frame is ©(f), where (ф, в, ip) are the rotation angles.
(X0, y0,Z0) = Ro(f) (13.1)
(<*>, в, xp) = 0(f) (13.2)
For example, in the case of a constant-velocity flow of speed in the positive x direction (in the wing’s frame of reference in Fig. 13.1) the function Ro(f)
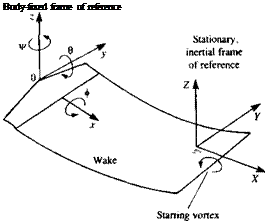 FIGURE 13.1
FIGURE 13.1
Inertial and body coordinates used to describe the motion of the body.
will be
(X0, Y0, Z„) = (~Uxt, 0, 0)
which means that the wing is being translated in the negative X direction.
The fluid surrounding the body is assumed to be inviscid, irrotational, and incompressible over the entire flow field, excluding the body’s solid boundaries and its wakes. Therefore, a velocity potential Ф(Л’, Y, Z) can be defined in the inertial frame and the continuity equation, in this frame of reference, becomes
V2<f> = 0 (in X, Y, Z coordinates) (13.3)
and the first boundary condition requiring zero normal velocity across the body’s solid boundaries is
(УФ + v) • n = 0 (in X, Y, Z coordinates) (13.4)
Here —v is the surface’s velocity and n = n(Ar, У, Z, f) is the vector normal to this moving surface, as viewed from the inertial frame of reference. (Note that v is defined with the minus sign so that the surface velocity will be positive in the body’s frame of reference.) Since Eq. (13.3) does not depend directly on time, the time dependency is introduced through this boundary condition (e. g., the location and orientation of n can vary with time). It is interesting to point out that Ф is the total velocity potential, but as a result of its definition in a frame that is attached to the undisturbed fluid its magnitude is small (in fact it is similar to the perturbation potential of Section 4.2).
The second boundary condition requires that the flow disturbance, due to the body’s motion through the fluid, should diminish far from the body (or wing in Fig. 13.1):
lim УФ = 0 (13.5)
|R-Rol—
where R = (X, Y, Z).
For the unsteady flow case the use of the Kelvin condition will supply an additional equation that can be used to determine the streamwise strength of the vorticity shed into the wake. In general, it states that in the potential flow region the angular momentum cannot change, thus the circulation Г around a fluid curve enclosing the wing and its wake is conserved:
jp
— = 0 (for any t) (13.6)
at
The solution of this problem, which becomes time-dependent because of the boundary condition (Eq. (13.4)), is easier in the body-fixed coordinate system. Consequently, a transformation f between the coordinate systems has to be established, based on the flight path information of Eqs. (13.1) and
(13.2) :
Such a transformation should include the translation and the rotation of the (x, y, z) system, and can be found in any basic dynamics text book and, for example, may have the form:
/x /1 0 0 / cos 0(f) 0 sin 0(f)
І у | = | 0 cos 0(f) – sin 0(f) If 0 1 О I
zj � sin 0(f) cos 0(f) /-sin0(f) 0 cos 0(f)/
cos 0(f) – sin 0(f) 0/X — X0 sin 0(f) cos 0(f) Ojl Y-Y0 I (13.7a)
0 0 l/Z-Zo/
Similarly, the kinematic velocity v of the surface due to the motion of the wing in Fig. 13.1, as viewed in the body frame of reference, is given by
v=—[Vo + fiXr] (13.8)
where V0 is the velocity of the (де, у, z) system’s origin, resolved into the instantaneous (x, y, z) directions
Уо = (ЛГ0, Y0,Z0) (13.9a)
Here r= (x, y, z) is the position vector and Q is the rate of rotation of the body’s frame of reference, as shown in Fig. 13.1,
П = (0,0,0) (13.9b)
In situations when an additional relative motion vre, within the (дг, у, z) system is desired (e. g., small-amplitude oscillation of a wing or its flap, in addition to the average motion of the body system) then Eq. (13.8) becomes
v= -[V0 + vrel + ftXr] (13.8a)
and
Vi = (x, y,z) (13.9c)
To an observer in the (x, y, z) frame, the velocity direction is opposite to the flight direction (as derived in the X, Y, Z frame) and therefore the minus sign appears in Eq. (13.8).
The proper transformation of Eqs. (13.3)-(13.5) into the body’s frame of reference requires the evaluation of the various derivatives in the (x, y, z) system. This can be found using the standard chain-rule differentiation and for example the 9/ dX term becomes
9 _ дх 9 ду 9 9z 9 ЭХ ~ 9X 9x + 9X Эу + ЭХ 9z
Here, 9x/9X, 9y/9X, 9z/9X include the information about the instantaneous orientation of the body-fixed frame of reference (it is also assumed that the time t is the same in both frames). For example, consider the case when the body frame of reference of Fig. 13.1 translates to the left and only one degree
But it is possible to transform Eqs. (13.3) and (13.4) into the body’s frame of reference without explicitly knowing Eq. (13.7) and still arrive at the same conclusions. For example, at any moment the continuity equation is independent of the coordinate system orientation and the mass should be conserved. Therefore, the quantity У2Ф is independent of the instantaneous coordinate system and the continuity equation in terms of (x, y, z) remains unchanged (the reader is encouraged to prove this by using the chain rule):
У2Ф = 0 (in x, y, z coordinates) (13.12)
Also, the two boundary conditions (Eqs. (13.4) and (13.5)) should state the same physical conditions. The gradient 7Ф will have the same magnitude and direction and the kinematic velocity v is given by Eq. (13.8) and therefore the zero-velocity normal to a solid surface boundary condition, in the body frame becomes
(УФ + v) • n = 0 (in jc, y, z coordinates) (13.13)
Here n is the normal to the body’s surface, in terms of the body coordinates (x, y, z).
By using Eq. (13.8a) with vrc, representing the motion of the body in the (x, y, z) coordinates, Eq. (13.13) becomes
(Уф — V0 – vre, – Я X r) • n = 0 (in x, y, z coordinates) (13.13a)
Note that this boundary condition can be derived directly by using Eq. (2.27) of Chapter 2. According to that terminology, the surface is defined in the body frame of reference by F as
F = z – r](x, y, t) = 0
Applying Eq. (2.24) (DF/Dt = 0) in the (X, Y, Z) coordinate system where the particles move with a velocity УФ yields
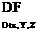 dF
dF
—-—(- УФ • V F = 0
dt
Transferring this expression into the (x, y, z) system requires the transformation of the dF/dt term by using Eq. (13.11) and with the second term remaining unchanged this becomes
9F
— – (V0 + ft X r) • VF + УФ • VF = 0
Recalling that in the body’s frame of reference dF/dt = – dr/dt and according to Eq. (2.26) VF/|VF| =n we get
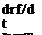 [УФ — (V0 + ft X r)]
[УФ — (V0 + ft X r)]
The last term represents the relative motion within the body’s frame of reference and by exchanging dr/dt/VF with a possible three-dimensional relative motion vrei • n we get
[УФ – (V0 + ft X r)] • n – vre| • n = 0
which is identical to the previous result of Eq. (13.13a).
In the case of more complex flowfields, when the modeling of nonzero velocity components across the boundaries is desired (e. g., engine inlet/exit flows or simulation of boundary layer displacement by blowing) a transpiration velocity VN can be added:
(УФ – V0- vrel – ft X r) • n= VN (13.136)
The most important conclusion from these results (Eqs. (13.12) and
(13.13) ) is that for incompressible flows the instantaneous solution is independent of time derivatives. That is, since the speed of sound is assumed to be infinite, the influence of the momentary boundary condition is immediately radiated across the whole fluid region. Therefore, steady-state solution techniques can be used to treat the time-dependent problem by substituting the instantaneous boundary condition (Eq. (13.13)) at each moment. The wake shape, however, does depend on the time history of the motion and consequently an appropriate vortex wake model has to be developed.
For many situations involving lifting problems the wake separation line has to be prescribed. As in the case of the steady-state flows the Kutta condition is assumed to be valid for the time-dependent case as well (for attached flows with reduced frequencies of less than 1 where the reduced a)L
frequency is defined in a manner similar to Eq. (1.52)). Therefore,
along trailing edges of lifting surfaces, the velocity has to be finite (to fix the
rear stagnation line) and
 УФ < oo (at trailing edges)
УФ < oo (at trailing edges)
![]() Ф(х, у, z) = – і – f цп • v(-) dS – j – [ a(-) dS (13.15)
Ф(х, у, z) = – і – f цп • v(-) dS – j – [ a(-) dS (13.15)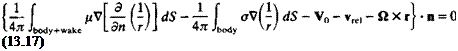











 FIGURE 13.1
FIGURE 13.1