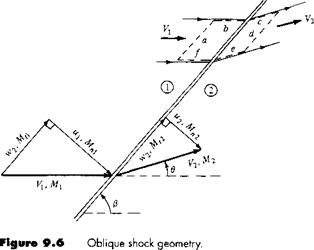
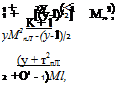Consider the oblique shock wave sketched in Figure 9.6. The angle between the shock wave and the upstream flow direction is defined as the wave angle, denoted by fl. The upstream flow (region 1) is horizontal, with a velocity V) and Mach number Mi – The downstream flow (region 2) is inclined upward through the deflection angle в and has velocity V2 and Mach number М2. The upstream velocity Vt is split into components tangential and normal to the shock wave, w and ji, respectively, with the associated tangential and normal Mach numbers Mtt and Mn,, respectively. Similarly, the downstream velocity is split into tangential and normal components W2 and /І2, respectively, with the associated Mach numbers M,2 and M„,2.
Consider the control volume shown by the dashed lines in the upper part of Figure 9.6. Sides a and d are parallel to the shock wave. Segments b and c follow the upper streamline, and segments e and / follow the lower streamline. Let us apply the integral form of the conservation equations to this control volume, keeping in mind that we are dealing with a steady, inviscid, adiabatic flow with no body forces. For these assumptions, the continuity equation, Equation (2.48), becomes
pV • dS = 0
s
This surface integral evaluated over faces a and d yields — pU A + p2u2A2, where A1 = A2 — area of faces a and d. The faces b, c, e, and / are parallel to the velocity,
and hence contribute nothing to the surface integral (i. e., V • dS = 0 for these faces). Thus, the continuity equation for an oblique shock wave is
PUA + P2U2A2 = 0
Keep in mind that u and U2 in Equation (9.2) are normal to the shock wave.
The integral form of the momentum equation, Equation (2.64), is a vector equation. Hence, it can be resolved into two components, tangential and normal to the shock wave. First, consider the tangential component, keeping in mind the type of flow we are considering:
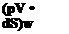
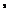
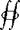
![Oblique Shock Relations Подпись: [9.3]](/img/3128/image143_2.png) (P d. S’)tangCntia|
(P d. S’)tangCntia|
In Equation (9.3), w is the component of velocity tangential to the wave. Since dS is perpendicular to the control surface, then (p dShangentiai over faces a and d is zero. Also, since the vectors p dS on faces b and / are equal and opposite, the pressure integral in Equation (9.3) involves two tangential forces that cancel each other over faces b and /. The same is true for faces c and e. Hence, Equation (9.3) becomes
![Oblique Shock Relations Подпись: [9.4]](/img/3128/image144_2.png) -(puxAx)w + (P2U2A2)w2 = 0
-(puxAx)w + (P2U2A2)w2 = 0
Dividing Equation (9.4) by Equation (9.2), we have
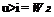 [9.5]
[9.5]
Equation (9.5) is an important result; it states that the tangential component of the flow velocity is constant across an oblique shock.
The normal component of the integral momentum equation is, from Equation (2.64),
![Oblique Shock Relations Подпись: [9.6]](/img/3128/image146_2.png) ’jlj’ (pV • dS)M = (pdS)normal
’jlj’ (pV • dS)M = (pdS)normal
s s
Here, the pressure integral evaluated over faces a and d yields the net sum —pA + P2A2. Once again, the equal and opposite pressure forces on b and / cancel, as do those on c and e. Hence, Equation (9.6) becomes, for the control volume shown in Figure 9.6,
-(ріИіАі)И] + (P2U2A2)U2 = -(-P1A1 + P2A2)
Since А і = A2, this becomes
Again, note that the only velocities appearing in Equation (9.7) are the components normal to the shock.
Finally, consider the integral form of the energy equation, Equation (2.95). For our present case, this can be written as
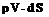
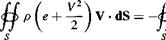 [9.8]
[9.8]
Again noting that the flow is tangent to faces b, c, /, and e, and hence V • dS = 0 on these faces, Equation (9.8) becomes, for the control volume in Figure 9.6,
~P (єі + у ^ щАх + P2 (e2 + y^ u2A2 = —{—pUA + P2U2A2) [9.9]
Collecting terms in Equation (9.9), we have
Dividing Equation (9.10) by (9.2), we have
V2 V2
hi + – j – = h2+ – j – [9.11]
Since h + V2/2 = h0, we have again the familiar result that the total enthalpy is constant across the shock wave. Moreover, for a calorically perfect gas, ho — cpTo‘, hence, the total temperature is constant across the shock wave. Carrying Equation
(9.11) a bit further, note from Figure 9.6 that V2 = u2 + w2. Also, from Equation
(9.5) , we know that иц = w2. Hence,
V2 — V22 = (и2 + w2) — (и2 + w) = u — u
Thus, Equation (9.11) becomes
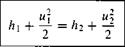 [9.12]
[9.12]
Let us now gather our results. Look carefully at Equations (9.2), (9.7), and (9.12). They are the continuity, normal momentum, and energy equations, respectively, for an oblique shock wave. Note that they involve the normal components only of velocity и і and u2, the tangential component w does not appear in these equations. Hence, we deduce that changes across an oblique shock wave are governed only by the component of velocity normal to the wave.
Again, look hard at Equations (9.2), (9.7), and (9.12). They are precisely the governing equations for a normal shock wave, as given by Equations (8.2), (8.6), and
(8.10) . Hence, precisely the same algebra as applied to the normal shock equations in Section 8.6, when applied to Equations (9.2), (9.7), and (9.12), will lead to identical expressions for changes across an oblique shock in terms of the normal component of the upstream Mach number Mn . Note that
![Oblique Shock Relations Подпись: [9.13]](/img/3128/image156_0.png) Mn. = M sin P
Mn. = M sin P
Hence, for an oblique shock wave, with Mn. given by Equation (9.13), we have, from Equations (8.59), (8.61), and (8.65),
The temperature ratio T2/T follows from the equation of state:
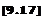 II – ElEL
II – ElEL
T pi p2
Note that Mn 2 is the normal Mach number behind the shock wave. The downstream Mach number itself, M2, can be found from Mn2 and the geometry of Figure 9.6 as
 Mn, 1
Mn, 1
sin(/l – 9)
Examine Equations (9.14) to (9.17). They state that oblique shock-wave properties in a calorically perfect gas depend only on the normal component of the upstream Mach number Mn.. However, note from Equation (9.13) that Mn. depends on both M and f. Recall from Section 8.6 that changes across a normal shock wave depend on one parameter only—the upstream Mach number M ,. In contrast, we now see that changes across an oblique shock wave depend on two parameters—say, M and
ft. However, this distinction is slightly moot because in reality a normal shock wave is a special case of oblique shocks where ft = ir/2.
Equation (9.18) introduces the deflection angle в into our oblique shock analysis; we need в to be able to calculate М2. However, 9 is not an independent, third parameter; rather, 9 is a function of M and ft, as derived below. From the geometry of Figure 9.6,
|
Mi
tan fi = —
|
[9.19]
|
|
Wi
|
|
|
and
|
М2
tan(£ – 0) = —
|
[9.20]
|
|
W2
|
|
Dividing Equation (9.20) by (9.19), recalling that wx = w2, and invoking the continuity equation, Equation (9.2), we obtain
tan(/l – 9) u2 pi
tan ft и і p2
![Oblique Shock Relations Подпись: [9.22]](/img/3128/image162.png) Combining Equation (9.21) with Equations (9.13) and (9.15), we obtain tan(/i – 9) 2+ (y — l)M2sin2/J
Combining Equation (9.21) with Equations (9.13) and (9.15), we obtain tan(/i – 9) 2+ (y — l)M2sin2/J
tan ft (y + l)Mf sin2 ft
which gives в as an implicit function of M and ft. After some trigonometric substitutions and rearrangement, Equation (9.22) can be cast explicitly for 9 as
Equation (9.23) is an important equation. It is called the в-fi-M relation, and it specifies 9 as a unique function of M and ft. This relation is vital to the analysis of oblique shock waves, and results from it are plotted in Figure 9.7 for у — 1.4. Examine this figure closely. It is a plot of wave angle versus deflection angle, with the Mach number as a parameter. The results given in Figure 9.7 are plotted in some detail—this is a chart which you will need to use for solving oblique shock problems.
Figure 9.7 illustrates a wealth of physical phenomena associated with oblique shock waves. For example:
1. For any given upstream Mach number M1, there is a maximum deflection angle 0max. If the physical geometry is such that 9 > 0max, then no solution exists for a straight oblique shock wave. Instead, nature establishes a curved shock wave, detached from the corner or the nose of a body. This is illustrated in Figure
9.8. Here, the left side of the figure illustrates flow over a wedge and a concave corner where the deflection angle is less than 0max for the given upstream Mach number. Therefore, we see a straight oblique shock wave attached to the nose of the wedge and to the comer. The right side of Figure 9.8 gives the case where the deflection angle is greater than 0max; hence, there is no allowable straight oblique shock solution from the theory developed earlier in this section. Instead, we have
|
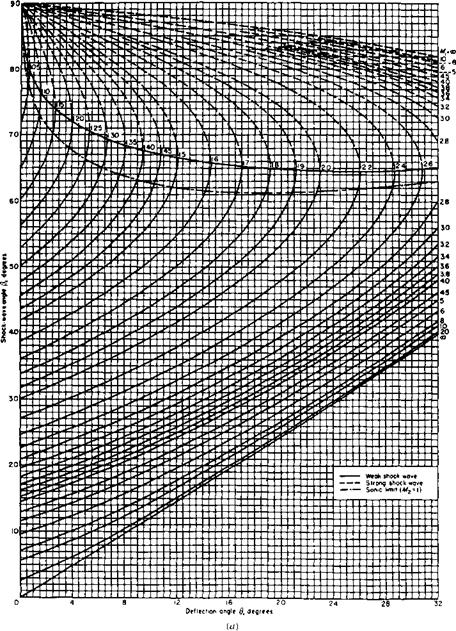
Figure 9.7 Oblique shock properties: у = 1.4. The в-fi-M diagram. (Source: NACA Report 1 135, Ames Research Staff, "Equations, Tables and Charts for Compressible Flow," 1953.)
|
|
Shock-wove angle 0, degree*
|
|
Figure 9.7 (continued) (Source: NACA Report 1 135, Ames Research Staff, "Equations, Tables and Charts for Compressible Flow," 1953.)
|
a curved shock wave detached from the nose of the wedge or from the comer. Return to Figure 9.7, and note that the value of 0max increases with increasing M. Hence, at higher Mach numbers, the straight oblique shock solution can exist at higher deflection angles. However, there is a limit; as M approaches infinity, #max approaches 45.5° (for у — 1.4).
2. For any given 9 less than 6>max, there are two straight oblique shock solutions for a given upstream Mach number. For example, if M = 2.0 and в = 15°, then from Figure 9.7, f5 can equal either 45.3 or 79.8°. The smaller value of f) is called the weak shock solution, and the larger value of fi is the strong shock solution. These two cases are illustrated in Figure 9.9. The classifications “weak” and “strong” derive from the fact that for a given M, the larger the wave angle, the larger the normal component of upstream Mach number МпЛ, and from Equation (9.16) the larger the pressure ratio pifp. Thus, in Figure 9.9, the higher-angle shock wave will compress the gas more than the lower-angle shock wave, hence the terms “strong” and “weak” solutions. In nature, the weak shock solution usually prevails. Whenever you see straight, attached oblique shock waves, such as sketched at the left of Figure 9.8, they are almost always the weak shock solution. It is safe to make this assumption, unless you have specific information to the contrary. Note in Figure 9.7 that the locus of points connecting all the values of 0max (the curve that sweeps approximately horizontally across the middle of Figure 9.7) divides the weak and strong shock solutions. Above
/
|
/
Figure 9.9 The weak and strong shock cases.
|
this curve, the strong shock solution prevails (as further indicated by the 9-fi-M curves being dashed); below this curve, the weak shock solution prevails (where the 9-fi-M curves are shown as solid lines). Note that slightly below this curve is another curve which also sweeps approximately horizontally across Figure 9.7. This curve is the dividing line above which М2 < 1 and below which М2 > 1. For the strong shock solution, the downstream Mach number is always subsonic M2 < 1. For the weak shock solution very near 0max, the downstream Mach number is also subsonic, but barely so. For the vast majority of cases involving the weak shock solution, the downstream Mach number is supersonic М2 > 1. Since the weak shock solution is almost always the case encountered in nature, we can readily state that the Mach number downstream of a straight, attached oblique shock is almost always supersonic.
3. If 9 = 0, then fi equals either 90° or /1. The case of /3 = 90° corresponds to a normal shock wave (i. e., the normal shocks discussed in Chapter 8 belong to the family of strong shock solutions). The case of fi — /z corresponds to the Mach wave illustrated in Figure 9.3b. In both cases, the flow streamlines experience no deflection across the wave.
4. (In all of the following discussions, we consider the weak shock solution exclusively, unless otherwise noted.) Consider an experiment where we have supersonic flow over a wedge of given semiangle 9, as sketched in Figure 9.10. Now assume that we increase the freestream Mach number M. As M increases, we observe that /1 decreases. For example, consider 9 — 20° and M = 2.0, as shown on the left of Figure 9.10. From Figure 9.7, we find that fi = 53.3°. Now assume M is increased to 5, keeping 9 constant at 20°, as sketched on the right of Figure 9.10. Here, we find that fi = 29.9°. Interestingly enough, although this shock is at a lower wave angle, it is a stronger shock than the one on the left. This is because Mn is larger for the case on the right. Although fi is smaller, which decreases Mn , the upstream Mach number M is larger, which increases M„ 1 by an amount which more than compensates for the decreased /3. For example, note the values of Mnд and Рг! P given in Figure 9.10. Clearly, the Mach 5 case on the right yields the stronger shock wave. Hence, in general for attached shocks with a fixed deflection angle, as the upstream Mach number M increases, the wave angle fi decreases, and the shock wave becomes stronger.
Going in the other direction, as Mi decreases, the wave angle increases, and the shock becomes weaker. Finally, if M is decreased enough, the shock wave will become detached. For the case of в = 20° shown in Figure 9.10, the shock will be detached for Mi < 1.84.
5. Consider another experiment. Here, let us keep M fixed and increase the deflection angle. For example, consider the supersonic flow over a wedge shown in Figure 9.11. Assume that we have M = 2.0 and в — 10°, as sketched at the left of Figure 9.11. The wave angle will be 39.2° (from Figure 9.7). Now assume that the wedge is hinged so that we can increase its deflection angle, keeping Mi constant. In such a case, the wave angle will increase, as shown on the right of Figure 9.11. Also, Mn will increase, and hence the shock will become stronger. Therefore, in general for attached shocks with a fixed upstream Mach number, as the deflection angle increases, the wave angle fi increases, and the shock becomes stronger. However, once в exceeds 0max, the shock wave will
become detached. For the case of M = 2.0 in Figure 9.11, this will occur when в > 23°.
The physical properties of oblique shocks just discussed are very important. Before proceeding further, make certain to go over this discussion several times until you feel perfectly comfortable with these physical variations.
Consider a supersonic flow with M = 2, p = 1 atm, and T = 288 K. This flow is deflected at a compression comer through 20°. Calculate M, p, T, p0, and T0 behind the resulting oblique shock wave.
Solution
From Figure 9.7, for Mi = 2 and в = 20°, ft = 53.4°. Hence, M„д = M sin ft = 2 sin 53.4° = 1.606. From Appendix B, for M„л = 1.60 (rounded to the nearest table entry),
Note: For oblique shocks, the entry for ро. г/P in Appendix В cannot be used to obtain po 2′, this entry in Appendix В is for normal shocks only and is obtained directly from Equation (8.80). In turn, Equation (8.80) is derived using (8.77), where M2 is the actual flow Mach number, not the normal component. Only in the case of a normal shock is this also the Mach number normal to the wave. Hence, Equation (8.80) holds only for normal shocks; it cannot be used for oblique shocks with Mi replaced by M„,i. For example, an incorrect calculation would be to use pop/Pi = 3.805 for МпЛ = 1.60. This gives />0 2 = 3.805 atm, a totally incorrect result compared with the correct value of 7.00 atm obtained above.
Example 9.2 | Consider an oblique shock wave with a wave angle of 30°. The upstream flow Mach number is 2.4. Calculate the deflection angle of the flow, the pressure and temperature ratios across the shock wave, and the Mach number behind the wave.
|
1. This is a fairly weak shock wave—only a 51 percent increase in pressure across the wave. Indeed, examining Figure 9.7, we find that this case is close to that of a Mach wave, where д = sin~'(l/M) = sin*1!^) = 24.6°. The shockwave angle of 30° is not much larger than д; the deflection angle of 6.5° is also small—consistent with the relative weakness of the shock wave.
2. Only two properties need to be specified in order to define uniquely a given oblique shock wave. In this example, M and fi were those two properties. In Example 9.1, the specified M and 9 were the two properties. Once any two properties about the oblique shock are specified, the shock is uniquely defined. This is analogous to the case of a normal shock wave studied in Chapter 8. There, we proved that all the changes across a normal shock wave were uniquely defined by specifying only one property, such as M. However, implicit in all of Chapter 8 was an additional property, namely, the wave angle of a normal shock wave is 90°. Of course, a normal shock is simply one example of the whole spectrum of oblique shocks, namely, a shock with /1 = 90°. An examination of Figure 9.7 shows that the normal shock belongs to the family of strong shock solutions, as discussed earlier.
|
Note: Once again, the oblique shock is uniquely defined by two properties, in this case fi and Pi/Pi-
Consider a Mach 3 flow. It is desired to slow this flow to a subsonic speed. Consider two separate ways of achieving this: (1) the Mach 3 flow is slowed by passing directly through a normal shock wave; (2) the Mach 3 flow first passes through an oblique shock with a 40° wave angle, and then subsequently through a normal shock. These two cases are sketched in Figure 9.12. Calculate the ratio of the final total pressure values for the two cases, that is, the total pressure behind the normal shock for case 2 divided by the total pressure behind the normal shock for case 1. Comment on the significance of the result.
Solution
For case 1, at M = 3, we have, from Appendix B,
() = 0.3283
V Po, ) case 1
For case 2, we have МпЛ = M, sin ft = 3 sin 40° = 1.93. From Appendix B,
= 0.7535 and Mn 2 = 0.588
Po, ‘
From Figure 9.7, for M, = 3 and ft = 40°, we have the deflection angle в = 22°. Hence,
From Appendix B, for a normal shock with an upstream Mach number of 1.9, we have Р03/Po2 = 0.7674. Thus, for case 2,
Figure 9.12 Illustration for Example 9.4.
The result of Example 9.4 shows that the final total pressure is 76 percent higher for the case of the multiple shock system (case 2) in comparison to the single normal shock (case 1). In principle, the total pressure is an indicator of how much useful work can be done by the gas; this is described later in Section 10.4. Everything else being equal, the higher the total pressure, the more useful is the flow. Indeed, losses of total pressure are an index of the efficiency of a fluid flow—the lower the total pressure loss, the more efficient is the flow process. In this example, case 2 is more efficient in slowing the flow to subsonic speeds than case 1 because the loss in total pressure across the multiple shock system of case 2 is actually less than that for case 1 with a single, strong, normal shock wave. The physical reason for this is straightforward. The loss in total pressure across a normal shock wave becomes particularly severe as the upstream Mach number increases; a glance at the P0.2/P0.1 column in Appendix В attests to this. If the Mach number of a flow can be reduced before passing through a normal shock, the loss in total pressure is much less because the normal shock is weaker. This is the function of the oblique shock in case 2, namely, to reduce the Mach number of the flow before passing through the normal shock. Although there is a total pressure loss across the oblique shock also, it is much less than across a normal shock at the same upstream Mach number. The net effect of the oblique shock reducing the flow Mach number before passing through the normal shock more than makes up for the total pressure loss across the oblique shock, with the beneficial result that the multiple shock system in case 2 produces a smaller loss in total pressure than a single normal shock at the same freestream Mach number.
A practical application of these results is in the design of supersonic inlets for jet engines. A normal shock inlet is sketched in Figure 9.13a. Here, a normal shock forms ahead of the inlet, with an attendant large loss in total pressure. In contrast, an oblique shock inlet is sketched in Figure 9. 3b. Here, a central cone creates an oblique shock wave, and the flow subsequently passes through a relatively weak normal shock at the lip of the inlet. For the same flight conditions (Mach number and altitude), the total pressure loss for the oblique shock inlet is less than for a normal shock inlet. Hence, everything else being equal, the resulting engine thrust will be higher for the oblique shock inlet. This, of course, is why most modem supersonic aircraft have oblique shock inlets.












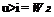 [9.5]
[9.5]