Fluid dynamics
1.1 Conservation laws

The conservation of mass for an infinitesimal material element of density p and volume V is given in the continuum approximation by [Batchelor (1967), Landau and Lifchitz (1987), Kundu (1990)]:
In integral form this equation becomes:
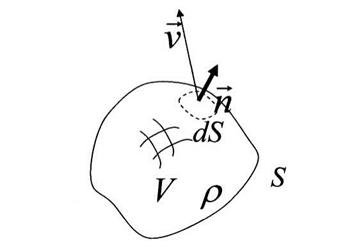
in which, V is a fixed control volume delimited by the surface S with outer unit normal П (Figure 1). The second law of Newton applied to an infinites-
![]()
|
imal material element is:
|
|
|
|
|
|
where f is the density of a force field acting on the bulk of the fluid and P is the stress tensor representing the surface interaction between the particle and its surroundings. Using the definition of the convective derivative (2) and the mass conservation law (5) we obtain the conservation form of the momentum equation:
where e is the internal energy of the fluid per unit of mass, v = |v| ,q the heat flux and Qw the energy production per unit volume.