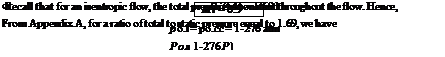Critical Mach Number
Return to the road map given in Figure 11.1. We have now finished our discussion of linearized flow and the associated compressibility corrections. Keep in mind that such linearized theory does not apply to the transonic flow regime, 0.8 < Мж <
1.2. Transonic flow is highly nonlinear, and theoretical transonic aerodynamics is a challenging and sophisticated subject. For the remainder of this chapter, we deal with several aspects of transonic flow from a qualitative point of view. The theory of transonic aerodynamics is beyond the scope of this book.
Consider an airfoil in a low-speed flow, say, with = 0.3, as sketched in Figure 11.5a. In the expansion over the top surface of the airfoil, the local flow Mach number M increases. Let point A represent the location on the airfoil surface
t Local MA
where the pressure is a minimum, hence where M is a maximum. In Figure 11.5a, let us say this maximum is MA = 0.435. Now assume that we gradually increase the freestream Mach number. As M^ increases, MA also increases. For example, if is increased to M = 0.5, the maximum local value of M will be 0.772, as shown in Figure 11.5b. Let us continue to increase Moo until we achieve just the right value such that the local Mach number at the minimum pressure point equals 1, that is, such that MA = 1.0, as shown in Figure 11.5c. When this happens, the freestream Mach number Mx is called the critical Mach number, denoted by Mcr. By definition, the critical Mach number is that freestream Mach number at which sonic flow is first achieved on the airfoil surface. In Figure 11.5c, Ma = 0.61.
One of the most important problems in high-speed aerodynamics is the determination of the critical Mach number of a given airfoil, because at values of Мж slightly above Mcr, the airfoil experiences a dramatic increase in drag coefficient (discussed in Section 11.7). The purpose of the present section is to give a rather straightforward method for estimating Mcr.
Let poo and pA represent the static pressures in the freestream and at point A, respectively, in Figure 11.5. For isentropic flow, where the total pressure po is constant, these static pressures are related through Equation (8.42) as follows:
Pa_ = Pa/Po = /1 + [(у-1)/2]Л^у/(у~П [11 56]
Рос Poc/Po l + [(y -)/2]Mj) *
The pressure coefficient at point A is given by Equation (11.22) as
Combining Equations (11.56) and (11.57), we have
Equation (11.58) is useful in its own right; for a given freestream Mach number, it relates the local value of Cp to the local Mach number. [Note that Equation (11.58) is the compressible flow analogue of Bernoulli’s equation, Equation (3.13), which for incompressible flow with a given freestream velocity and pressure relates the local pressure at a point in the flow to the local velocity at that point.] However, for our purposes here, we ask the question, What is the value of the local Cp when the local Mach number is unity? By definition, this value of the pressure coefficient is called the critical pressure coefficient, denoted by Cp. cr. For a given freestream Mach number Moo, the value of Cp. cr can be obtained by inserting MA = 1 into Equation (11.58):
Equation (11.59) allows us to calculate the pressure coefficient at any point in the flow where the local Mach number is 1, for a given freestream Mach number M^. For example, if Mx is slightly greater than Mcr, say, Mx = 0.65 as shown in Figure
11.5d, then a finite region of supersonic flow will exist above the airfoil; Equation
(11.59) allows us to calculate the pressure coefficient at only those points where M = 1, that is, at only those points that fall on the sonic line in Figure 11,5d. Now, returning to Figure 11.5c, when the freestream Mach number is precisely equal to the critical Mach number, there is only one point where M = 1, namely, point A. The pressure coefficient at point A will be Cp<cr, which is obtained from Equation (11.59). In this case, Moo in Equation (11.59) is precisely Mcr. Hence,
[1 1.60]
Equation (11.60) shows that Cpa is a unique function of Mcr; this variation is plotted as curve C in Figure 11.6. Note that Equation (11.60) is simply an aerodynamic relation for isentropic flow—it has no connection with the shape of a given airfoil. In this sense, Equation (11.60), and hence curve C in Figure 11.6, is a type of “universal relation” which can be used for all airfoils.
Equation (11.60), in conjunction with any one of the compressibility corrections given by Equations (11.51), (11.54), or (11.55), allows us to estimate the critical Mach number for a given airfoil as follows:
1. By some means, either experimental or theoretical, obtain the low-speed incompressible value of the pressure coefficient Cpq at the minimum pressure point on the given airfoil.
2. Using any of the compressibility corrections, Equation (11.51), (11.54), or
(11.55) , plot the variation of Cp with Moo■ This is represented by curve В in Figure 11.6.
Eq. (11.51), (11.54), or (11.55)
cr
3. Somewhere on curve B, there will be a single point where the pressure coefficient corresponds to locally sonic flow. Indeed, this point must coincide with Equation (11.60), represented by curve C in Figure 11.6. Hence, the intersection of curves В and C represents the point corresponding to sonic flow at the minimum pressure location on the airfoil. In turn, the value of M^ at this intersection is, by definition, the critical Mach number, as shown in Figure 11.6.
The graphical construction in Figure 11.6 is not an exact determination of MCT. Although curve C is exact, curve В is approximate because it represents the approximate compressibility correction. Hence, Figure 11.6 gives only an estimation of MCT. However, such an estimation is quite useful for preliminary design, and the results from Figure 11.6 are accurate enough for most applications.
Consider two airfoils, one thin and the other thick, as sketched in Figure 11.7. First consider the low-speed incompressible flow over these airfoils. The flow over the thin airfoil is only slightly perturbed from the freestream. Hence, the expansion over the top surface is mild, and Cp о at the minimum pressure point is a negative number of only small absolute magnitude, as shown in Figure 11.7. [Recall from Equation
(11.32) that Cp ос й; hence, the smaller the perturbation, the smaller is the absolute magnitude of Cp.] In contrast, the flow over the thick airfoil experiences a large perturbation from the freestream. The expansion over the top surface is strong, and Cp (t at the minimum pressure point is a negative number of large magnitude, as shown in Figure 11.7. If we now perform the same construction for each airfoil as given in Figure 11.6, we see that the thick airfoil will have a lower critical Mach number than
the thin airfoil. This is clearly illustrated in Figure 11.7. For high-speed airplanes, it is desirable to have Mcr as high as possible. Hence, modern high-speed subsonic airplanes are usually designed with relatively thin airfoils. (The development of the supercritical airfoil has somewhat loosened this criterion, as discussed in Section
11.8. ) For example, the Gates Lear jet high-speed jet executive transport utilizes a 9 percent thick airfoil; contrast this with the low-speed Piper Aztec, a twin-engine propeller-driven general aviation aircraft designed with a 14 percent thick airfoil.
Example 1 1 .3 I In this example, we illustrate the estimation of the critical Mach number for an airfoil using (a) the graphical solution discussed in this section, and (b) an analytical solution using a closed – form equation obtained from a combination of Equations (11.51) and (11.60). Consider the NACA 0012 airfoil at zero angle of attack shown at the top of Figure 11.8. The pressure coefficient distribution over this airfoil, measured in a wind tunnel at low speed, is given at the
|
c Figure 1 1.8 Low-speed pressure coefficient distribution over the surface of an NACA 0012 airfoil at zero angle of attack. Re = 3.65 x 106. (Source; R. J. Freuler and G. M. Gregorek, "An Evaluation of Four Single Element Airfoil Analytical Methods," in Advanced Technology Airfoil Research, NASA CP 2045, 1978, pp. 133-162.) |
Following step three, these values are plotted as Curve В in Figure 11.9. The intersection of curves В and C is at point D. The freestream Mach number associated with point D is the critical Mach number for the NACA 0012 airfoil. From Figure 11.9, we have
(.b) Analytical Solution. In Figure 11.9, curve В is given by Equation (11.61)
At the intersection point D, (Cp)mill in Equation (11.61) is the critical pressure coefficient and Moo is the critical Mach number
Cp a = 0,43 (at point D) [11.62]
Vі – Mcr
Also, at point D the value of Cp, cr is given by Equation (11.60). Hence, at point D we can equate the right-hand sides of Equations (11.62) and (11.60),
-0.43 _ _j?_ [( +[(y – 1)/2]МС2ГУ/У ‘
yi^Mj У Ml [ 1 + (y – l)/2 J
Equation (11.63) is one equation with one unknown, namely, Mcr. The solution of Equation (11.63) gives the value of Mcr associated with the intersection point D in Figure 11.9, that is, the solution of Equation (11.63) is the critical Mach number for the NACA 0012 airfoil. Since Mcr appears in a complicated fashion on both sides of Equation (11.63), we solve the equation by trial-and-error by assuming different values of Mcr, calculating the values of both sides of Equation (11.63), and iterating until we find a value of Ma that results in both the right and left sides being the same value.
м -0.43 2 ГП+[(у-])/2]МІу/г-‘ _ ~
СГ 1 + (к — l)/2 ) _
|
0.72 |
-0.6196 |
-0.6996 |
|
0.73 |
-0.6292 |
-0.6621 |
|
0.74 |
-0.6393 |
-0.6260 |
|
0.738 |
-0.6372 |
-0.6331 |
|
0.737 |
-0.6362 |
-0.6367 |
|
0.7371 |
-0.6363 |
-0.6363 |
To four-place accuracy, when Mcr = 0.7371, both the left and right sides of Equation (11.63) have the same value. Therefore, the analytical solution yields
Note: Within the two-place accuracy of the graphical solution in part (a), both the graphical and analytical solutions give the same value of Mcr.
Question: How accurate is the estimate of the critical Mach number in this example? To answer this question, we examine some experimental pressure coefficient distributions for the NACA 0012 airfoil obtained at higher freestream Mach numbers. Wind tunnel measurements of the surface pressure distributions for this airfoil at zero angle of attack in a high-speed flow are shown in Figure 11.10; for Figure 11.10a, Mx = 0.575, and for Figure ll. lOfc,
|
(a) |
|
(h) Figure 11.10 Wind tunnel measurements of surface pressure coefficient distribution for the NACA 0012 airfoil at zero angle of attack. Experimental data of Frueler and Gregorek, NASA CP 2045. (a) Мх = 0.575, (b) Moo = 0.725. |
Mx = 0.725. In Figure 11.10a, the value of Cpxr = -1.465 at = 0.575 is shown as the dashed horizontal line. From the definition of critical pressure coefficient, any local value of Cp above this horizontal line corresponds to locally supersonic flow, and any local value below the horizontal line corresponds to locally subsonic flow. Clearly from the measured surface pressure coefficient distribution at Mx = 0.575 shown in Figure 11.10a, the flow is
locally subsonic at every point on the surface. Hence, Mж = 0.575 is below the critical Mach number. In Figure 1 l. lOh, which is for a higher Mach number, the value of C pa = —0.681 at Moo = 0.725 is shown as the dashed horizontal line. Here, the local pressure coefficient on the airfoil is higher than Cpxr at every point on the surface except at the point of minimum pressure, where (Cp)mi„ is essentially equal to Cp, cl. This means that for = 0.725, the flow is locally subsonic at every point on the surface except the point of minimum pressure, where the flow is essentially sonic. Hence, these experimental measurements indicate that the critical Mach number of the NACA 0012 airfoil at zero angle of attack is approximately 0.73. Comparing this experimental result with the calculated value of Mcr = 0.74 in this example, we see that our calculations are amazingly accurate, to within about one percent.











 p = 0.9329po = 0.9329(2116)
p = 0.9329po = 0.9329(2116)
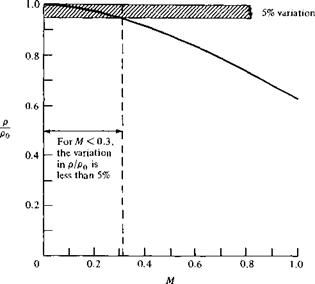
 M = 0.6
M = 0.6