Conclusion
[1]As mentioned in chapter 2, this assumption can not be done in the case of future large dimension transport aircrafts.
since the problem of computing the exact value of ц is known to be NP hard.
[2] We can now come back to the original problem, which is to transform the uncertain closed loop of Figure 1.3 into the standard interconnection structure M(s) – A(s) of Figure 1.1. This is very easy, since M(s) is simply the transfer matrix, which is seen by the model perturbation Д(я) on Figure 1.3 (i. e. the transfer between w and z).
[3] More generally, if the closed loop contains m neglected dynamics A{ (s), it can be transformed into the standard interconnection structure M(s) — A(s) with:
A(s) = diag(Ai(s),…, Am(s)) (1.10)
The unit ball ДДД is introduced in the space of transfer matricesA(s): BA(s) – {Д00 = diag(Ai(s),.. .,Am(s)) ||A(s)||oo < 1} (1-П)
‘The parametric uncertainties 5j may enter in practice in numerous other ways the (state – space or input/output) plant model. See chapter 3 for more details.
[4]the degree a of stability of a state-space matrix A is defined as a = max; Re(Xi(A)), where W) is an eigenvalue of A.
[5]An other reason for handling repeated complex scalars is historical: during the Eighties, the real repeated scalars were often assumed to be complex, because the real nature of parametric uncertainties could not be taken into account by existing computational algorithms.
[6] The usefulness of /X bounds is now explained. For the sake of clarity, we restrict our attention to the case of a real model perturbation
[7]For historical reasons, the special case of a complex model perturbation can be included in the general case of a mixed model perturbation.
[8]The LFT of equation (7.3) is assumed to be well-posed despite the uncertainties in Д2.
[9]See also chapter 11 (subsection 1.1) for the definition of a one-sided uncertainty.
[10] Condition (10.28) in the above Proposition can be simply rewritten as a {Hu) < 1, which is equivalent to the condition ст(Мц) < 1 in Lemma 4..1.
• Let Д2 = 6u>Im. The assumption к < І/^дЛМгг) in Lemma 4..1 means that the LFT Fi(H(u}o),8ujIm) (or equivalentlyi?;(fl’,8u>Im) since #22 = H22) is well-posed: see the discussion in subsection 4.2.
• Lemma 4..1 can thus be applied. Equation det{I — бшН) = Ocan be rewritten as det(l/8u>I – H) = 0, which means that the 8ш’s satisfying this last equation are the inverses of the eigenvalues of TL.
[11]It could also be interesting to consider the alternative problem, which is to compute the maximal size of the model uncertainties, for which a robust delay margin is guaranteed.
[12] The robust delay margin is to be computed, i. e. the minimal value of the MIMO delay margin when the model perturbation A belongs to its unit ball (see the end of subsection 1.2). With reference to equation (11.7), this reduces to the computation at each frequency of Ді is indeed to be maintained inside its unit ball J5Ai, while the rcj’s in A2 are to be expanded in [0, к]. Note indeed that xt є [0, k is equivalent to ті Є [0,r] in the relation:
[13] Alternatively, the singularity ofthe matrix I~P2i(jiL)A2 means that the LFT Р,(Р0’«).Да) is not well-posed.
[14] Some results in (Katebi and Zhang, 1995) are recalled here. See this reference for details. We come back to the problem of subsection 2.1 (see also Figure 12.1). The issue is to take into account the super har-
[15]The/i lower bound by (Dailey, 1990) is used in this section. Because the real model uncertainty Д2 ally contains 3 parametric uncertainties, this ^ lower bound coincides with the exact value of ц.
The general aim of this book was to emphasize the usefulness of the p approach for practical robustness analysis problems. The p and skewed p tools were first introduced. Their efficiency was then illustrated through realistic examples, namely a flight control system for a civil aircraft, a missile autopilot and a telescope mock-up.
Consider an LTI plant subject to LTI model uncertainties. These ones can be divided into two main categories, namely the parametric uncertainties (which more generally represent the uncertainties in the plant dynamics inside the control bandwidth) and the neglected dynamics (which represent the uncertainties outside the control bandwidth). Assuming that a controller was synthesized with the nominal model of the plant, the issue is to study the effect of these uncertainties on the closed loop stability and performance properties.
It was shown in chapters 1 and 7 that the s. s.v. P and its skewed version z’ provide a general framework for treating most of the robust stability and performance problems. The only requirement is to transform the closed loop with all its uncertainties into a standard interconnection structure: in this context, the main problem is to account for the parametric uncertainties, which may enter the open loop plant model in numerous ways. It is most generally possible to transform the plant model with its parametric uncertainties into a standard form, namely an LFT (part 2).
In chapter 7, it was emphasized that large classes of p problems, such as robust performance analysis, are skewed p problems, i. e. a single application of the /z tool provides in these cases just a robustness test. A recursive application of the /z tool is thus necessary to compute the robustness margin. Because of the practical usefulness of these skewed p problems, a much more efficient solution is to directly compute a bound
of the skewed s. s.v. u.
Various methods were thus presented in chapter 8 for computing bounds of the skewed s. s.v. v, while chapter 5 described methods for computing bounds of the classical 5.5. v. p. These techniques can be classified according to 3 different criteria:
■ nature of the result: upper and lower bounds of the (skewed) s. s.v. are generally computed instead of the exact value, the main reason being the computational requirement.
■ nature of the model uncertainties: when the problem only contains parametric uncertainties, the associated model perturbation is said to be real. On the contrary, this model perturbation is complex if there are only neglected dynamics. In the general case of parametric uncertainties and neglected dynamics, the associated model perturbation is said to be mixed. A great deal of work has been devoted to the computation of (a bound of) the real s. s.v.. On the other hand, methods for computing bounds of the complex s. s.v. have been lately extended to the mixed case.
■ Computational requirement: the algorithms are either polynomial time, or exponential time, i. e. the computational burden is a polynomial or exponential function of the size of the problem.
All methods in chapters 5 and 8 were evaluated on the aeronautical examples, and it was illustrated that the robustness margin can be computed with a satisfactory accuracy, even for large dimension problems: in the context of a problem involving a large number of uncertainties, our approach was to compute lower and upper bounds of this margin using polynomial time algorithms. Even if the gap between these bounds can not be guaranteed a priori, it appears reasonable in our realistic examples.
As a final point, the usefulness of the p and skewed p tools was briefly illustrated in part 5 for three non standard problems:
■ A computationally efficient method was proposed, for directly computing an interval of the maximal s. s.v. over a frequency interval. Good results were obtained in the examples, and an accurate estimate of the robustness margin was computed.
■ The issue was then to analyze the robustness properties of a closed loop in the face of parametric uncertainties, neglected dynamics and uncertain time delays. This is not a classical problem, since delays do not correspond to classical LTI finite-dimensional transfer functions.
It is nevertheless possible to parameterize the frequency response of these delays in order to reduce the problem to a standard // problem.
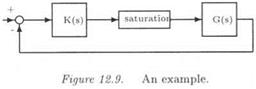
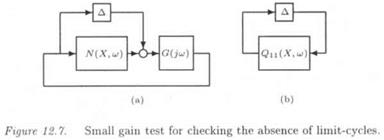
■ Let a linear closed loop system with additional separable nonlinearities (e. g. saturations). Classical methods exist for detecting the presence or the absence of limit-cycles in this closed loop. The /л approach enables to extend these classical methods to the case of parametric uncertainties entering the linear part of the closed loop.











 s2 + 1.4s + 1
s2 + 1.4s + 1
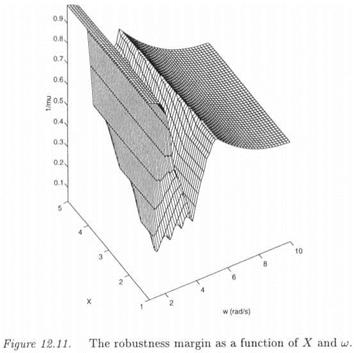
 Remark: remember first that r(X, ui) represents the minimal size of the model perturbation Д 2 , for which a limit-cycle is obtained at [Х, ш) (see definition 3..2). In the context of the above design problem, a limit-cycle is obtained for the nominal value of the controller, and this controller is retuned in order to move the limit-cycle at a point (X, u>): it is thus interesting to use the minimal size model perturbation associated to r(X, w). Indeed, the corresponding controller can be considered as the controller, which is the closest to the nominal one, and which moves the limit-cycle at (X, ci).
Remark: remember first that r(X, ui) represents the minimal size of the model perturbation Д 2 , for which a limit-cycle is obtained at [Х, ш) (see definition 3..2). In the context of the above design problem, a limit-cycle is obtained for the nominal value of the controller, and this controller is retuned in order to move the limit-cycle at a point (X, u>): it is thus interesting to use the minimal size model perturbation associated to r(X, w). Indeed, the corresponding controller can be considered as the controller, which is the closest to the nominal one, and which moves the limit-cycle at (X, ci).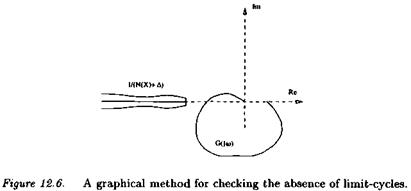
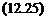 -ГТ = max_ /j, A2{Fu{P(ju>),N{X, u>))) r(u) xe[x, x]
-ГТ = max_ /j, A2{Fu{P(ju>),N{X, u>))) r(u) xe[x, x]
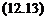 l-Fi(P(ju>),A2)N(X, u) =0
l-Fi(P(ju>),A2)N(X, u) =0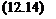 det(I – Fl(P(juJ),A2)N(X, u)) = 0
det(I – Fl(P(juJ),A2)N(X, u)) = 0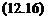 det(I — P22{juj)A2) ф 0 УД2 Є kD2
det(I — P22{juj)A2) ф 0 УД2 Є kD2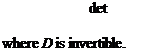 {c d) = det(D)det(A ~ BD~lC) (12.12)
{c d) = det(D)det(A ~ BD~lC) (12.12)