DESIGNING NEW AEROFOILS
A mathematical method of working out new ordinates, starting from a chosen camber line and a symmetrical thickness form, is given in the standard text, Theory of Wing Sections by Abbott and Von Doenhoff. Although not a quick procedure, the calculations required are not difficult Failing this method, a modeller may devise his own wing sections by the graphical method outlined in Fig. A 8. The camber line is plotted first then at each station a circle is drawn, the radius being taken from the ordinates for the thickness form, and the centre being on the camber line at the appropriate point Finally a smooth curve is drawn tangentially to aU the circles and the nose radius to produce the aerofoil.
WORKING OUT THE CAMBER
Many aerofoil designations contain information about camber and thickness. The NACA systems are described in Chapter 7, with further information in Abbott and Von
Doenhoff as above. The Benedek Aerofoils give the camber, in percent of chord in the last digit, thus В 10355 is cambered 5 percent, 8356, 6 percent and so on. The first figure gives the profile thickness, the central figure or figures the position of the maximum thickness point, hence Benedek В 12355 is 12% thick at 35%, and cambered 5%.
In other cases it is sometimes possible to work out the maximum camber arithmetically. This is applicable only where the aerofoil ordinates are based on a chord • line running through the leading edge and trailing edge. In these cases, by finding the thickness of the profile at a number of stations and subtracting half this figure, at each place, from the upper surface ordinate, the approximate ordinate for the camber line is found and the maximum value then easily discovered. Note that in finding the profile thickness in this way, minus signs below the chord line must be allowed for. This method of halving the thickness will not produce accurate ordinates for the aerofoil camber line, especially near the nose and trailing edge, but it will produce a correct figure for the maximum camber and its location.
The camber of other aerofoils, plotted on tangential chord lines or on other arbitrary reference lines, may be estimated by measuring from the plotted profile. The true chord line, nose to trailing edge, must first be drawn in, then the half thickness plotted as accurately as possible, and the camber measured.
More accurate estimates of camber from the ordinates may – be carried out by somewhat more complex arithmetic, but this is seldom necessary.
Fig. A8 Fig. A8
|
i take ordinates of desired camber line, and plot. ii take radii ot circles from desired thickness and draw on arc as shown. Hi draw smooth curved lines tangential to circles. INDEX OF AEROFOILS |
Mean lines, low drag bodies and symmetrical profiles are grouped at the beginning of this section. The N. A. C. A. ‘6’ thickness forms are arranged in order of increasing laminar flow (min. pressure point at 30, 40, 50% chord etc), and in increasing thickness (6, 9, 10, 12, 15, 18% etc.) In the section devoted to cambered profiles, the N. A. C. A. 6 series aerofoils are arranged in order of increasing thickness (9 to 18%), then by increasing camber (shown by the third figure from the right which indicates the ‘ideal’ ci in tenths -.2, .3, .4, .6 etc), and then by increasing proportion of laminar flow (given by the second digit from the left, 30%, 40%, 50% etc.) The various letters and other additions indicate minor modifications to the profiles (e. g., A =0.5 indicates the use of A = 0.5 mean line instead of the usual A = 1).
|
MEAN LINES
|
|
REFLEX MEAN LINE FOR ZERO PITCHING MOMENT SCALE TO REQUIRED CAMBER |
NACA 210 MEAN LINE CL IDEAL 0.3
NACA A ** 0.0 MEAN LINE
|
NACA A – 0.6 MEAN LINE |
0.9 MEAN LINE
|
NACA A – 1.0 MEAN LINE |
МАСА 0010 L. E. radius
1.10 Percent
МАСА 0009 L E. radius
0.89 Percent
|
Chord |
Upper |
Chord Lower |
|
Station Surface |
Station Surface |
|
|
XU |
vu |
XL YL |
|
.000 |
.000 |
.000 .000 |
|
.500 |
.749 |
.500 -.749 |
|
.750 |
.906 |
.750 -.906 |
|
1.350 |
U151 |
1.350 -1.151 |
|
3.500 |
1.583 |
3.500 -1.583 |
|
5.000 |
3.196 |
5.000 -3.198 |
|
7.500 |
3.655 |
7.500 -3.655 |
|
10.000 |
3.034 |
10.000 -3.034 |
|
15.000 |
3.591 |
15.000 -3.591 |
|
30.000 |
3.997 |
30.000 -3.997 |
|
30.000 |
4.443 |
30.000 -4.443 |
|
40.000 |
4.447 |
40.000 -4.447 |
|
50.000 |
4.056 |
50.000 -4.056 |
|
60.000 |
3.358 |
60.000 -3.358 |
|
70.000 |
3.458 |
70.000 -3.458 |
|
80.000 |
1.471 |
80.000 -1.471 |
|
90.000 |
.550 |
90.000 -.550 |
|
95.000 |
.196 |
95.000 -.196 |
|
100.000 |
.000 |
100.000 .000 |
|
Chord |
Upper |
Chord |
Lower |
|
Station Surface |
Station |
Surface |
|
|
XU |
YU |
XL |
YL |
|
.000 |
.000 |
.000 |
.000 |
|
.050 |
.160 |
.050 |
-.160 |
|
.100 |
.340 |
.100 |
-.240 |
|
.300 |
.350 |
.300 |
-.350 |
|
.400 |
.500 |
.400 |
-.500 |
|
.500 |
.503 |
.500 |
-.503 |
|
.750 |
.609 |
.750 |
-.609 |
|
1350 |
.771 |
1.250 |
-.771 |
|
3.500 |
1.057 |
2.500 |
-1.057 |
|
5.000 |
1.463 |
5.000 |
-1.462 |
|
7.500 |
1.766 |
7.500 |
-1.766 |
|
10.000 |
3.010 |
10.000 |
-2.010 |
|
15.000 |
3.386 |
15.000 |
-2386 |
|
30.000 |
3.656 |
20.000 |
-2.656 |
|
30.000 |
3.954 |
30.000 |
-2.954 |
|
40.000 |
2.971 |
40.000 |
-2.971 |
|
50.000 |
2.723 |
60.000 |
-2.723 |
|
60.000 |
2.267 |
60.000 |
-2.267 |
|
70.000 |
1.670 |
70.000 |
-1.670 |
|
80.000 |
1.008 |
80.000 |
-1.008 |
|
90.000 |
.383 |
90.000 |
-.383 |
|
95.000 |
.138 |
95.000 |
-.138 |
|
100.000 |
.000 |
100.000 |
.000 |
|
Chord |
Upper |
Chord Lower |
|
Station |
Surface |
Station Surface |
|
XU |
YU |
X ■< r |
|
.000 |
.000 |
.000 .000 |
|
300 |
.620 |
300 -.620 |
|
.400 |
.910 |
.400 -.910 |
|
.600 |
1.130 |
.600′ -1.120 |
|
900 |
1.350 |
.800 -1.250 |
|
1350 |
1.578 |
1.350 -1.578 |
|
2.500 |
2.178 |
2.500 -2.178 |
|
5.000 |
2.962 |
5.000 -3.962 |
|
7.500 |
3.500 |
7.500 -3.SOO |
|
10.000 |
3.902 |
10.000 -3.902 |
|
15.000 |
4.455 |
15.000 -4.455 |
|
20.000 |
4.782 |
30.000 -4.782 |
|
25.000 |
4.952 |
35.000 -4.953 |
|
30.000 |
5.002 |
30.000 -5.003 |
|
40.000 |
4337 |
40.000 -4337 |
|
50.000 |
4.412 |
50.000 -4.412 |
|
60.000 |
3303 |
60.000 -3303 |
|
70.000 |
3.053 |
70.000 -3.053 |
|
80.000 |
2.187 |
80.000 -2.187 |
|
90.000 |
1.207 |
90.000 -1.207 |
|
95.000 |
.672 |
95.000 -.672 |
|
100.000 |
.105 |
100.000 -.105 |
|
Chord |
Upoer |
Chord |
Lower |
|
Stanon! |
Surface |
Station Surface |
|
|
XU |
YU |
XL |
YL |
|
.000 |
.000 |
000 |
000 |
|
.200 |
490 |
.700 |
– 490 |
|
.400 |
.870 |
400 |
– 870 |
|
.600 |
1 010 |
.600 |
■1 0Ю |
|
.800 |
1.170 |
BOO |
-1 170 |
|
1 250 |
1.420 |
1.750 |
-1 470 |
|
3.500 |
1.961 |
2500 |
-1 961 |
|
s. ooo |
3666 |
5.000 -7666 |
|
|
7.500 |
3.150 |
7 500 -3 150 |
|
|
10.000 |
3512 |
10.000 – 3517 |
|
|
15.000 |
4.009 |
15.000 -4.009 |
|
|
20.000 |
4.303 |
30.000 -4 303 |
|
|
25.000 |
4.456 |
25.000 -4.456 |
|
|
30.000 |
4.501 |
30.000 -4.501 |
|
|
40.000 |
4.352 |
40000 -4 357 |
|
|
50.000 |
3.971 |
50.000 -3.971 |
|
|
60.000 |
3.423 |
60.000 -3.473 |
|
|
70.000 |
2.748 |
70.000 – 2.748 |
|
|
80.000 |
1.967 |
80.000 -1.967 |
|
|
90.000 |
1.086 |
90.000 -1.086 |
|
|
95.000 |
.605 |
95.000 -.605 |
|
|
100.000 |
.095 |
100.000 -.095 |
NACA 63 009
XL YL.000 .000 M0 – IMS.7» -1.837
1.350 -3.537
3.500 -3.577
5.0 -5.0S5
7.600 -5.183
10.0 -7880
15.0 -8.441
30.0 -9410
30.0 -10413
40.0 -10.398
50.0 -9JOS
80.0 -7441
70.0 -5390
80800 -3.064
90.0 -1.113
95.0 -.392
100.000 .000
NACA 64 0Ю LE RADIUS 0.720 PERCENT
NACA 64 000 LE RA0IUS 0.576 PERCENT
|
NACA 65 A 006 |
NACA 65 006 |
NACA 64 2 016 L. E. rebut 1.590 Percent |
NACA 64 1012 |
|||||||||
|
Chord |
Upper |
Chord Lower |
Chord |
Upper |
Chord |
Lower |
Chord |
Upper |
Chord Lower |
Chord |
Upper |
Chord Lower |
|
Station |
Surface |
Station Surface |
Station Surface |
Station |
Surface |
Station |
Surface |
Station Surface |
Station |
Surface |
Station Surface |
|
|
XU |
YU |
XL YL |
XU |
YU |
XL |
YL |
XU |
YU |
XL YL |
XU |
YU |
XL YL |
|
800 |
.000 |
.000 .000 |
800 |
.000 |
.000 |
.000 |
800 |
800 |
800 .000 |
.000 |
.000 |
800 800 |
|
.500 |
.615 |
800 -815 |
800 |
.476 |
.500 |
-.476 |
800 |
1808 |
800 -1808 |
800 |
878 |
800 -878 |
|
.750 |
.746 |
.750 -.746 |
.750 |
874 |
.750 |
-.574 |
.750 |
1.456 |
.750 -1/456 |
750 |
1.179 |
.750 -1.179 |
|
1.260 |
851 |
1850 -851 |
I860 |
.717 |
1850 |
-.717 |
I860 |
1842 |
1850 -1842 |
I860 |
1.490 |
I860 -1.490 |
|
2800 |
1.303 |
2800 -1803 |
2800 |
.956 |
2800 |
-856 |
2800 |
2828 |
2800 -2828 |
2800 |
2.035 |
2800 -2835 |
|
5.000 |
1.749 |
5.000 -1.749 |
5.000 |
1.310 |
5.000 |
-1810 |
5800 |
3804 |
5800 -3.604 |
6.000 |
2810 |
5800 -2810 |
|
7800 |
2.120 |
7.500 -2.120 |
7800 |
1869 |
7800 |
-1.589 |
7800 |
4840 |
7800 -4840 |
7800 |
3894 |
7800 -3894 |
|
10.000 |
2.432 |
10.000 -2.432 |
10800 |
1824 |
10.000 |
-1824 |
10.000 |
4842 |
10.000 -4842 |
10800 |
3871 |
10800 -3871 |
|
15.000 |
2826 |
16800 -2826 |
15.000 |
2.197 |
16800 |
-2.197 |
15800 |
5.786 |
15800 -6.785 |
15800 |
4820 |
15.000 -4820 |
|
20800 |
3.301 |
20.000 -3.301 |
20.000 |
2.482 |
20.000 |
-2.482 |
20800 |
6.480 |
20.000 -6.480 |
20800 |
6.173 |
20800 -5.173 |
|
30800 |
3.791 |
30.000 -3.791 |
30800 |
2852 |
30.000 |
-2852 |
30800 |
7819 |
30800 -7819 |
30.000 |
5844 |
30800 -5844 |
|
40.000 |
3895 |
40800 -3.995 |
40.000 |
2888 |
40800 |
-2888 |
40800 |
7.473 |
40.000 -7.473 |
40800 |
5881 |
40800 -5881 |
|
50.000 |
3895 |
60.000 -3895 |
50800 |
2800 |
50.000 |
.-2800 |
50800 |
6810 |
50800 -6810 |
50.000 |
5.480 |
50800 -5.480 |
|
60800 |
3.456 |
60800 -3.456 |
60800 |
2818 |
60.000 |
-2818 |
60800 |
6820 |
60800 -8820 |
60800 |
4848 |
60.000 -4.548 |
|
70.000 |
2.763 |
70.000 -2.763 |
70800 |
1835 |
70.000 |
-1835 |
70.000 |
4.113 |
70800 -4.113 |
70800 |
3850 |
70.000 -3860 |
|
80.000 |
1898 |
80.000 -1898 |
80800 |
1833 |
80800 |
-1833 |
80800 |
2.472 |
80.000 -2.472 |
80800 |
2.029 |
80800 -2.009 |
|
90.000 |
860 |
90.000 -860 |
90800 |
810 |
90800 |
-810 |
90.000 |
850 |
90800 -.950 |
90800 |
.786 |
90800 -.785 |
|
95.000 |
.489 |
96800 -.489 |
95.000 |
.195 |
95800 |
-.195 |
95800 |
846 |
95800 -845 |
95800 |
286 |
95.000 -886 |
|
100.000 |
818 |
100800 -.018 |
100.000 |
800 |
100.000 |
.000 2 |
100.000 93 |
800 |
100.000 800 > |
100.000 |
800 |
100800 800 |
|
NACA 65 3 018 L. E. radtu* |
|
XL YL.000 .000 600 – 765 .750 *628 1650 -1.163 2600 -1.673 5.000 -2.182 7600 -2.650 10.0 -3.040 15.0 -3658 20.0 -4.127 30.0 -4.742 40.0 -4.995 50.0 -4663 60.0 -4604 70600 -3.432 80.0 -2.332 90.0 -1.188 95.0 – 604 100.000 -.021 |
Wortmenn FX LIIM42/K 25
For 25 percent flep
CLARK Y
Gottingen 548
(1930 to 1950 period)
Gottingen 804 (Eppler EA 8 (-11
-12 06) L. E. radius.5 camber 0.67
at SO
|
Chord |
Upper |
Chord |
Lamar |
Chard |
Upper |
Chord Lower |
|
Station Surface |
Station |
Surface |
Station |
Surface |
Station Surface |
|
|
XU |
YU |
XL |
YL |
XU |
YU |
XL YL |
|
.000 |
OOO |
.000 |
.000 |
.000 |
OOO |
OOO OOO |
|
.000 |
050 |
.200 |
*.430 |
OOO |
1000 |
000 – ooo |
|
200 |
1050 |
.400 |
-000 |
.400 |
1060 |
OOO -.770 |
|
MO |
2000 |
.600 |
‘040 |
OOO |
.1800 |
OOO ‘050 |
|
Я00 |
2.270 |
OOO |
‘060 |
OOO |
0060 |
OOO ‘1.120 |
|
1250 |
1730 |
1050 |
-1030 |
1050 |
2.440 |
1060 -1.430 |
|
2.S00 |
3000 |
2000 |
‘1040 |
2000 |
3.390 |
2000 -1060 |
|
SJOOO |
6060 |
5000 |
-1.990 |
5.000 |
4.730 |
6.000 -2.490 |
|
7900 |
6.570 |
7000 |
‘2050 |
7000 |
5.780 |
7000 ‘2.740 |
|
10900 |
7080 |
10.000 |
‘1090 |
10.000 |
8090 |
10000 -2060 |
|
15.000 |
9.180 |
15.000 |
‘1070 |
15000 |
7080 |
15000 -2080 |
|
20.000 |
10040 |
20000 |
-1060 |
20000 |
8000 |
20.000 ‘2.740 |
|
»j000 |
11.140 |
25000 |
-.780 |
25000 |
9010 |
25000 ‘2000 |
|
30.000 |
11050 |
30000 |
-080 |
30000 |
9.780 |
30000 -2060 |
|
40900 |
IIOOO |
40000 |
OOO |
40000 |
9000 |
40.000 -1000 |
|
50000 |
11.180 |
50000 |
050 |
80000 |
9.190 |
50000 ‘1.400 |
|
60Л00 |
9050 |
60000 |
.780 |
80000 |
9.140 |
60.000 -1.000 |
|
70.000 |
8030 |
70000 |
050 |
70.000 |
6080 |
70000 -050 |
|
80000 |
6030 |
80000 |
.730 |
80000 |
4080 |
80000 – 090 |
|
90.000 |
Э. ЗЭ0 |
90.000 |
.390 |
90.000 |
2.710 |
90000 *230 |
|
95.000 |
1.790 |
95.000 |
.180 |
95000 |
1.470 |
95000 -130 |
|
100000 |
.120 |
100000 |
-.120 |
100.000 |
.130 |
100.000 -.180 |
|
Chord |
Upper |
Chord Lower |
Chord |
Upper |
Chord |
Lower |
|
Station |
Surface |
Station Surface |
Station |
Surface |
Station |
Surface |
|
XU |
YU |
XL YL |
XU |
YU |
XL |
YL |
|
OOO |
OOO |
OOO.000 |
.000 |
OOO |
.000 |
.000 |
|
OOO |
020 |
OOO ‘.610 |
1008 |
1094 |
1.402 |
-1.448 |
|
.400 |
1.280 |
OOO ‘OOO |
2.297 |
2.411 |
2.703 |
-1027 |
|
OOO |
1010 |
OOO ‘1.100 |
4.742 |
3.420 |
5058 |
-2.462 |
|
OOO |
1.730 |
OOO ‘1091 |
7317 |
4.168 |
7.783 |
-2009 |
|
1.260 |
2.150 |
1050 -1060 |
9.710 |
4.786 |
10090 |
-3.016 |
|
2.600 |
2080 |
2000 ‘2070 |
14.722 |
5065 |
15078 |
-3.227 |
|
5000 |
4.130 |
5.000 -3.010 |
19.781 |
6076 |
20039 |
-3076 |
|
7000 |
4080 |
7000 ‘3.480 |
24014 |
6.668 |
25.166 |
-3.230 |
|
10000 |
6030 |
10.000 -3.750 |
29076 |
6075 |
30.125 |
-3.125 |
|
15000 |
6010 |
15000 -4.100 |
40000 |
6037 |
40.000 |
-2037 |
|
20.000 |
7060 |
20.000 ‘4030 |
50.049 |
6.356 |
49051 |
-2.468 |
|
25.000 |
7070 |
25.000 -4.220 |
60.005 |
5.580 |
59015 |
-2.024 |
|
30000 |
7080 |
30.000 -4.120 |
79.W2 |
4.551 |
89098 |
‘1.551 |
|
40.000 |
7000 |
40000 ‘3000 |
80087 |
3.296 |
79003 |
-1 074 |
|
60000 |
7040 |
50000 -3040 |
90087 |
1016 |
89033 |
-.594 |
|
60000 |
6080 |
80000 ‘2.780 |
95.041 |
090 |
94059 |
-.352 |
|
70.000 |
5.180 |
70.000 ‘2.140 |
100000 |
.105 |
IOOOOO |
-.105 |
|
80000 |
3.750 |
80.000 -1.600 |
||||
|
90000 |
2.080 |
90000 -020 |
||||
|
95000 |
1.140 |
96.000 -.480 |
||||
|
100.000 |
.130 |
100.000 -.130 |
|
NACA 4415 LE RAOIUS 2.49 PERCENT
|
|
Chord |
Upper |
Chord |
Lower |
Chord |
Upper |
Chord Lower |
Chord |
Tppar |
Chord |
14МЄГ |
Chord |
Upper |
Chord |
Lower |
|
Station |
Surface |
Station |
Surface |
Station Surface |
Station Surface |
Station Surface Station |
urface |
Station |
Surface |
Station |
Surface |
|||
|
XU |
YU |
XL |
YL |
XU |
YU |
XL YL |
XU |
YU |
XL |
YL |
XU |
YU |
XL |
YL |
|
.000 |
.000 |
.000 |
.000 |
.000 |
.000 |
.000 .000 |
.000 |
.000 |
.000 |
.000 |
.000 |
400 |
400 |
.000 |
|
450 |
402 |
450 |
-478 |
499 |
473 |
401 -.723 |
.424 |
466 |
470 |
-.744 |
.423 |
468 |
477 |
-756 |
|
М2 |
1.112 |
418 |
-.796 |
.638 |
1.068 |
462 -458 |
4S5 |
1444 |
.035 |
-488 |
464 |
1.058 |
436 |
-.900 |
|
1.0S9 |
1.451 |
1.441 |
-409 |
1.123 |
1.379 |
1.377 -1.067 |
1.153 |
1442 |
1447 |
-1.100 |
1.151 |
1487 |
1449 |
-1.125 |
|
2476 |
2495 |
2.724 |
-1451 |
2.353 |
1461 |
2447 -1.403 |
2457 |
1455 |
2413 |
-1.473 |
2454 |
1444 |
2416 |
-1422 |
|
4.740 |
3.034 |
5451 |
-1492 |
4437 |
2.759 |
5.163 -1447 |
4474 |
2465 |
6.126 |
-1463 |
4405 |
2.769 |
5.131 |
-2.047 |
|
7.230 |
3465 |
7.770 |
-1419 |
7432 |
3.436 |
7468 -2.164 |
7469 |
3455 |
7.931 |
-2416 |
7464 |
3.400 |
7453 |
-2.428 |
|
9.737 |
4490 |
10463 |
-1496 |
9432 |
3.970 |
10.168 -2.420 |
9459 |
3.792 |
10.132 |
-2400 |
•463 |
3417 |
10.137 |
-2.725 |
|
14.748 |
5466 |
15452 |
-2444 |
14442 |
4419 |
15.158 -2409 |
14474 |
4482 |
20.116 |
-3430 |
14469 |
4.729 |
15.131 |
-3.157 |
|
10.770 |
6.126 |
20430 |
-2.406 |
19459 |
6.464 |
20.141 -3475 |
19485 |
5400 |
10.116 |
-3440 |
19482 |
5428 |
20.118 |
-3.469 |
|
24,800 |
6.705 |
25400 |
-2.499 |
24479 |
6446 |
25.121 -3462 |
24400 |
5456 |
25.100 |
-3464 |
24498 |
5.764 |
25.102 |
-3462 |
|
29434 |
7.13» |
30.166 |
-2437 |
29.902 |
6494 |
30498 -3478 |
29417 |
5.994 |
30.083 |
-3.688 |
29.916 |
6.060 |
30.064 |
-3.764 |
|
34471 |
7.414 |
35.129 |
-2.518 |
34427 |
6413 |
35473 -3.423 |
34435 |
6.192 |
35405 |
-3.744 |
34436 |
6419 |
36465 |
-3.771 |
|
39410 |
7452 |
40.090 |
-2.436 |
39452 |
6401 |
40.048 -3489 |
35455 |
6474 |
40.045 |
-3.718 |
39456 |
9447 |
40.045 |
-3489 |
|
44450 |
7422 |
46.050 |
-2.266 |
44477 |
6436 |
45.023 -3452 |
44475 |
6406 |
46.026 |
-3.680 |
44.976 |
9.151 |
45425 |
-3423 |
|
40009 |
7444 |
50.011 |
-2424 |
50.000 |
6434 |
50.000 -3.030 |
45475 |
6414 |
50405 |
-3464 |
49.994 |
5443 |
50.005 |
-3483 |
|
60.067 |
6424 |
69443 |
-1.418 |
60.039 |
5427 |
69461 -2.415 |
50425 |
6423 |
59472 |
-2.719 |
90.029 |
5445 |
50472 |
-2.641 |
|
70.108 |
5.490 |
69492 |
-.760 |
70.063 |
4.584 |
69437 -1468 |
70454 |
4410 |
•9445 |
-1.944 |
70.052 |
4427 |
09448 |
-1461 |
|
90.151 |
3.967 |
79449 |
-429 |
80470 |
3496 |
79.930 -.908 |
50.076 |
3407 |
79424 |
-1.167 |
90.074 |
2.974 |
79426 |
-1.104 |
|
90.104 |
2438 |
90496 |
-.076 |
90466 |
1436 |
89444 -.296 |
80.062 |
1.551 |
85445 |
-471 |
90.090 |
1419 |
•9460 |
-439 |
|
95.053 |
1428 |
94447 |
-.048 |
96.038 |
1414 |
94482 -485 |
96427 |
.795 |
94474 |
-405 |
95.029 |
.769 |
94.974 |
-479 |
|
100.000 |
421 |
100.000 |
-.021 |
100.000 |
.021 |
100.000 -.021 |
100.000 |
421 |
100.000 |
-421 |
100.000 |
.021 |
100.000 |
-.021 |
|
МАСА 63-1-212 |
г 2 2 о |
e 1 |
МАСА 94-A410 ІАЦ>4МОО) |
|||||||||||
|
Chord |
Upper |
Chord |
Lower |
Chord |
Upper |
Chord Lower |
Chord |
Upper |
Chord |
Lower |
Chord |
Upper |
Chord |
Lower |
|
Station Surface |
Station |
Surface |
Station |
Surface |
Station Surface |
Station |
Surface |
Station |
Surface |
Station Surface |
Station |
Surface |
||
|
XU |
YU |
XL |
YL |
XU |
YU |
XL YL |
XU |
YU |
XL |
YL |
XU |
YU |
XL |
YL |
|
.000 |
.000 |
.000 |
.000 |
400 |
400 |
400 400 |
.000 |
.000 |
400 |
.000 |
400 |
400 |
.000 |
.000 |
|
.417 |
1.032 |
.583 |
-432 |
.435 |
419 |
485 -.712 |
415 |
477 |
.795 |
-427 |
414 |
479 |
.786 |
-426 |
|
JS57 |
1460 |
443 |
-1.120 |
478 |
499 |
422 -459 |
494 |
1461 |
1418 |
-499 |
481 |
1j550 |
1419 |
-.666 |
|
1.145 |
1422 |
1.355 |
-1.408 |
1.169 |
1473 |
1431 -1469 |
2472 |
2.470 |
2428 |
-.799 |
2.084 |
2.476 |
2439 |
-.767 |
|
2478 |
2494 |
2422 |
-1412 |
2.408 |
1.757 |
2492 -1485 |
4420 |
3405 |
5.480 |
-466 |
4408 |
3.719 |
5.494 |
-432 |
|
4453 |
3438 |
5.137 |
-2406 |
4498 |
2.491 |
5.102 -1469 |
7403 |
4450 |
7497 |
-453 |
8484 |
4.703 |
8419 |
-411 |
|
7458 |
3463 |
7442 |
-3.115 |
7494 |
3489 |
7406 -2421 |
9403 |
5.457 |
10.457 |
-.434 |
9.479 |
6441 |
10421 |
-.771 |
|
9459 |
4454 |
10.141 |
-3420 |
9494 |
3456 |
10.106 -2421 |
14430 |
6414 |
16.470 |
-.756 |
14.500 |
•402 |
16400 |
-456 |
|
14488 |
5.470 |
15.132 |
-4.124 |
14499 |
4438 |
16.101 -2492 |
10479 |
7433 |
20.422 |
-496 |
16443 |
7468 |
20.457 |
-.526 |
|
19482 |
6.137 |
20.118 |
-4445 |
19409 |
4438 |
20491 -3446 |
24439 |
6420 |
25451 |
-.595 |
24401 |
8.795 |
25499 |
-483 |
|
34400 |
6.606 |
25.100 |
-4416 |
24421 |
6497 |
26479 -3407 |
29.707 |
0402 |
30 493 |
-.454 |
29468 |
9.420 |
30432 |
-432 |
|
29420 |
6401 |
30490 |
-4457 |
29436 |
5.732 |
30484 -3.788 |
34.790 |
9.596 |
35420 |
-.328 |
34.742 |
9457 |
35459 |
-.065 |
|
34441 |
7430 |
35450 |
-4470 |
34451 |
6454 |
35.049 -3494 |
39455 |
9413 |
40.145 |
-.174 |
38420 |
10.107 |
40.190 |
.123 |
|
39482 |
6491 |
40438 |
-4449 |
39.966 |
8467 |
40432 -3425 |
44430 |
9422 |
45470 |
.034 |
44.900 |
10.150 |
45.100 |
.354 |
|
44482 |
9.799 |
45.018 |
-4409 |
44494 |
6488 |
45418 -3488 |
50400 |
9449 |
60400 |
400 |
49477 |
10405 |
80.023 |
437 |
|
90.000 |
6.473 |
50400 |
-4467 |
50.000 |
5416 |
50400 -3.709 |
00.117 |
9439 |
50453 |
401 |
•0.114 |
9425 |
89496 |
1.187 |
|
80429 |
5.491 |
59471 |
-3449 |
80427 |
6417 |
59473 -3476 |
70.150 |
7.496 |
50411 |
1453 |
70415 |
7450 |
69.795 |
1410 |
|
70443 |
4.182 |
69457 |
-2438 |
70443 |
4.128 |
89457 -2.194 |
•0405 |
6475 |
79.792 |
1.495 |
•0400 |
5419 |
79.700 |
1457 |
|
80442 |
2498 |
79.958 |
-1.109 |
90444 |
2.793 |
79458 -1.191 |
50.166 |
3475 |
•9435 |
1477 |
90404 |
3.004 |
89.799 |
420 |
|
90425 |
1.224 |
99.975 |
-.190 |
90428 |
1427 |
89472 -493 |
•6.112 |
1451 |
94488 |
493 |
•5.104 |
1412 |
•4499 |
.450 |
|
95.012 |
468 |
94498 |
496 |
95414 |
422 |
94496 410 |
100400 |
.009 |
100.000 |
400 |
100.000 |
421 |
100400 |
-.021 |
|
100400 |
400 |
100.000 |
.000 |
100.000 |
400 |
100400 400 |
|
МАСА 64-А-410 |
|
МАСА 64^910 |
|
МАСА 64^.210 |
|
МАСА вЗА-210 |
Chord Lower Station Surface
XL VL.000 300
MO -.350 .400 -.410 300 -.560 1.250 -500 2.500 -1500
5.0 -2300
10.0 -3300
20.0 -4.000 30300 -5.000
40.0 -4.900
50.0 -4.500
60.0 -4300 70300 -3.500
80.0 -2300 90300 -1.500
100.000 .000
Sigurd Isaacson 53507 L. E. radius 0.5 percent
Sigurd Isaacson 64009 L. E. radius 0.3 percent
Sigurd Isaacson 73508 L. E. radius 0.4 percent
Sigurd Isaacson 53009 L. E. radius 0.8 percent
|
Benedek 894OSB LE. radio* |
|
Benedek В669вС L. E. radius |
Benedek 995668 LE. radios |
Benedek 984S6F |
Benedek 8635568 L. E. radius |
||||||||||||
|
0Л Percent |
0.7 Percent |
0.7 Percent |
|||||||||||||
|
Chord |
Ifooer |
Chord |
Lower |
Chord |
Upper |
Chord |
Lower |
Chord |
Upper |
Chord |
.ewer |
Chord Upper Chord Lower |
|||
|
Station Surface |
Station |
Surface |
Station |
Surface |
Station |
Surface |
Station Surface Station Surface |
Station Surface Station Surface |
|||||||
|
XU |
YU |
XL |
YL |
XU |
YU |
XL |
YL |
XU |
YU |
XL |
YL |
XU |
YU |
XL |
YL |
|
.000 |
1.000 |
.000 |
1.000 |
300 |
1.000 |
.000 |
1300 |
.000 |
.760 |
.000 |
.750 |
.000 |
.700 |
.000 |
.700 |
|
.200 |
1.450 |
.200 |
.590 |
300 |
(300 |
300 |
300 |
.200 |
1310 |
.200 |
.320 |
.200 |
1.200 |
.200 |
320 |
|
.400 |
1.700 |
.400 |
.440 |
.400 |
1.770 |
300 |
360 |
.400 |
1300 |
.400 |
.160 |
.400 |
1.400 |
.400 |
.080 |
|
jBOO |
1.900 |
.900 |
.480 |
.600 |
1.960 |
300 |
300 |
300 |
1330 |
300 |
.090 |
300 |
1300 |
.700 |
.000 |
|
JBOO |
2.100 |
300 |
.330 |
300 |
2.150 |
300 |
.280 |
300 |
2.100 |
300 |
.030 |
300 |
1.800 |
.800 |
310 |
|
1.250 |
2.500 |
1.250 |
350 |
1350 |
2300 |
1350 |
300 |
1.250 |
2.600 |
1.250 |
.000 |
1.250 |
2.180 |
1.250 |
.030 |
|
2.800 |
3.400 |
2300 |
.000 |
2300 |
3300 |
2300 |
.000 |
2.500 |
3.900 |
2.500 |
.200 |
2.500 |
3.140 |
2.500 |
.150 |
|
5.000 |
4.600 |
5.000 |
.200 |
5.000 |
4.280 |
5300 |
360 |
5.000 |
4.950 |
6300 |
.500 |
6.000 |
4.550 |
6.000 |
.420 |
|
7.800 |
5.400 |
7.500 |
.450 |
7.500 |
5300 |
7300 |
.400 |
7300 |
6.000 |
7.500 |
300 |
7300 |
5350 |
7.500 |
.780 |
|
10.000 |
9.160 |
10.000 |
.750 |
10.000 |
5.750 |
10300 |
.700 |
10300 |
6.900 |
10.000 |
1.100 |
10.000 |
6.530 |
10.000 |
1.120 |
|
15.000 |
7.250 |
15.000 |
1.300 |
15,000 |
6300 |
15300 |
1.200 |
15300 |
8300 |
15.000 |
1.500 |
16.000 |
7.780 |
16000 |
1.850 |
|
30.000 |
8.000 |
20.000 |
1300 |
20.000 |
7.700 |
20.000 |
1.750 |
20.000 |
8.700 |
20.000 |
2.200 |
20.000 |
8.550 |
20.000 |
2.450 |
|
25.000 |
9.550 |
25.000 |
2.350 |
25.000 |
8300 |
25300 |
2.250 |
25.000 |
8.950 |
25.000 |
2300 |
25.000 |
9.000 |
25.000 |
2.920 |
|
30.000 |
8.980 |
30.000 |
2.700 |
30.000 |
8.750 |
30300 |
2300 |
30300 |
9.000 |
30300 |
3.250 |
30.000 |
9.150 |
30.000 |
3350 |
|
40.000 |
9.400 |
40300 |
3360 |
40300 |
9.150 |
40300 |
3300 |
40300 |
8.900 |
40.000 |
4.000 |
40.000 |
8.990 |
40.000 |
3370 |
|
80.000 |
9.300 |
50.000 |
3300 |
50.000 |
9.100 |
50300 |
3.750 |
50.000 |
8300 |
50300 |
4.500 |
50.000 |
8.230 |
50.000 |
3350 |
|
00.000 |
8.750 |
60.000 |
4.000 |
60.000 |
8350 |
60300 |
3360 |
60.000 |
7.500 |
50.000 |
4.500 |
60.000 |
7.100 |
80.000 |
3.500 |
|
70.000 |
7.950 |
70.000 |
3300 |
70300 |
7300 |
76.000 |
3300 |
70.000 |
6.400 |
70.000 |
4.050 |
70.000 |
3750 |
70.000 |
3.000 |
|
80.000 |
5.900 |
80.000 |
2350 |
80.000 |
6.000 |
80.000 |
3.000 |
80.000 |
5.060 |
80300 |
3.300 |
80.000 |
4.080 |
80.000 |
2.220 |
|
90.000 |
3.550 |
90.000 |
1.500 |
90.000 |
3.700 |
90300 |
1.750 |
90.000 |
3.700 |
90.000 |
2.000 |
90.000 |
2.230 |
90.000 |
1.190 |
|
96.000 |
2.000 |
95.000 |
300 |
98300 |
2.100 |
95300 |
350 |
95.000 |
2.600 |
95300 |
1.100 |
100.000 |
320 100.000 |
.000 |
|
|
100.000 |
.400 |
100.000 |
.000 |
100.000 |
.450 |
100.000 |
.000 |
100.000 |
.500 |
100.000 |
.000 |
||||
|
Benedek 993569 L. E. radius |
Benedek 883068 L. E. radius |
Benedek 974560 |
Benedek 87406F |
||||||||||||
|
0 A Percent |
0.9 Percent |
||||||||||||||
|
Chord |
Upper |
Chord |
Lower |
Chord Upper |
Chord |
Lower |
Chord |
Upper |
Chord |
Lower |
Chord |
Upper |
Chord |
Lower |
|
|
Station |
Surface |
Station |
Surface |
Station Surface Station |
Surface |
Station |
Surface |
Station |
Surface |
Station |
Surface |
Station |
Surface |
||
|
XU |
YU |
XL |
YL |
XU |
YU |
XL |
YL |
XU |
YU |
XL |
YL |
XU |
YU |
XL |
YL |
|
.000 |
1.110 |
300 |
1.110 |
.000 |
1.180 |
.000 |
1.180 |
.000 |
350 |
.000 |
350 |
.000 |
300 |
.000 |
.900 |
|
.000 |
1.400 |
.200 |
.MO |
.200 |
1.740 |
.200 |
300 |
.200 |
1350 |
.200 |
350 |
.200 |
1.500 |
.200 |
.420 |
|
.200 |
1.810 |
.400 |
Ж |
.400 |
2.050 |
.400 |
.420 |
.400 |
1320 |
.400 |
350 |
.400 |
1.900 |
.400 |
.300 |
|
.400 |
2.070 |
300 |
.390 |
.900 |
2.310 |
.600 |
320 |
.600 |
1330 |
300 |
.ISO |
.600 |
2.200 |
300 |
.220 |
|
300 |
2.530 |
300 |
.300 |
300 |
2350 |
.800 |
.270 |
300 |
2.080 |
.800 |
.030 |
300 |
2.490 |
300 |
.170 |
|
1.250 |
3.000 |
1.250 |
.170′ |
1.250 |
3.020 |
1.260 |
.170 |
1350 |
2.500 |
1.250 |
.000 |
1350 |
2.950 |
1.250 |
.100 |
|
2.500 |
4.150 |
2300 |
.030 |
2300 |
4.110 |
2.500 |
.000 |
2.500 |
3.480 |
2.500 |
.200 |
2.500 |
3.950 |
2.500 |
.100 |
|
5.000 |
5330 |
5.000 |
.050 |
5.000 |
5330 |
5.000 |
.070 |
5.000 |
4.900 |
5.000 |
.450 |
5.000 |
5.800 |
5.000 |
.450 |
|
7.500 |
7.090 |
7.600 |
.250 |
7.500 |
7.130 |
7.500 |
380 |
7.500 |
5.950 |
7.500 |
.700 |
7300 |
8.800 |
7.500 |
300 |
|
10.000 |
8.000 |
10.000 |
.500 |
ta. ooo |
8.180 |
10.000 |
.960 |
10.000 |
6.700 |
10.000 |
350 |
10.000 |
7.400 |
10.000 |
1.000 |
|
18.000 |
9.150 |
15300 |
1.190 |
15300 |
9.500 |
16.000 |
1.470 |
15.000 |
8.000 |
15.000 |
1.450 |
16.000 |
8.550 |
16000 |
1.500 |
|
20.000 |
9370 |
20.000 |
1370 |
20.000 |
10.220 |
20.000 |
2.130 |
20.000 |
8.700 |
20.000 |
1350 |
20.000 |
8.200 |
20.000 |
1.950 |
|
25.000 |
10380 |
25300 |
2350 |
25.000 |
10310 |
25.000 |
2.560 |
25.000 |
9.000 |
25.000 |
2.600 |
25300 |
9.580 |
25.000 |
2.400 |
|
30.000 |
10.370 |
30.000 |
2.700 |
30.000 |
10300 |
30.000 |
2.830 |
30.000 |
9350 |
30.000 |
3.000 |
30.000 |
9.850 |
30.000 |
2300 |
|
40.000 |
9.910 |
40.000 |
3.050 |
40.000 |
9.900 |
40.000 |
3.000 |
40.000 |
8300 |
40.000 |
4.000 |
40.000 |
9.300 |
40.000 |
3.400 |
|
60.000 |
8380 |
50.000 |
2.980 |
«0.000 |
8330 |
50.000 |
2.900 |
50.000 |
8.000 |
50.000 |
4.500 |
50.000 |
9.800 |
50.000 |
3300 |
|
90.000 |
7.500 |
90.000 |
2.670 |
60.000 |
7.470 |
60.000 |
2.820 |
60.000 |
6300 |
60.000 |
4.000 |
60.000 |
7.700 |
60.000 |
3.750 |
|
70.000 |
5.900 |
70.000 |
2.220 |
70.000 |
5350 |
70.000 |
2.170 |
70.000 |
5.500 |
70.000 |
3.000 |
70.000 |
8350 |
70.000 |
3.400 |
|
80.000 |
4.200 |
80.000 |
1320 |
80.000 |
4.150 |
80.000 |
1.530 |
60.000 |
3.950 |
80.000 |
2.000 |
80.000 |
5.400 |
80.000 |
2350 |
|
90.000 |
2320 |
90.000 |
390 |
90.000 |
2.330 |
90.000 |
.830 |
90.000 |
2350 |
90.000 |
1.000 |
90.000 |
3.950 |
90.000 |
1.600 |
|
100.000 |
.330 |
100.000 |
.000 |
100.000 |
.350 |
100.000 |
.000 |
95.000 |
1.400 |
95.000 |
.500 |
95.000 |
2.900 |
95.000 |
.900 |
|
100.000 |
.500 |
100300 |
.000 |
100.000 |
.500 |
100.000 |
.000 |
|
Benedek 885578 I E. rediu* 0.6 Percent |
|
Banadak 883088 LE. radiu* 0.7 Percent |
|
.000 .400 .000 .790 .200 1.000 .400 1.220 800 1800 1.290 1.970 2800 3.000 9.000 4.730 7.900 8.170 10.0 7830 19.0 9.*20 20.0 10890 29800 10.470 30.0 10830 40800 10830 90.0 9.470 90.0 8.200 70.0 8.800 80800 4870 90.0 2.900 100.000 .100 |
|
Pfenning Laminar 11 LE. radiu* 08 Percent |
|
AIRFOIL |
64 |
6.45* |
2*00 |
e. oo |
AIRFOIL 65 |
e |
•88« |
6.00 |
|||
|
N |
A |
Y |
N |
A |
T |
||||||
|
V-DISTR. FOR |
the above |
ALPHA REL |
. ZERO-LIFT LINE |
||||||||
|
0 |
00000 |
0.0000Q |
0*862 |
0*854 |
0 |
1.00006 |
0 |
00000 |
J7»19 |
0.S7T |
|
|
l |
99679 |
0*00076 |
0*891 |
0*888 |
1 |
0.99660 |
0 |
00070 |
0.699 |
0.895 |
|
|
2 |
98761 |
0*00311 |
0*947 |
0*948 |
2 |
0.96762 |
0 |
00260 |
0.969 |
0.951 |
|
|
Э |
9t324 |
0*00686 |
1*006 |
1*013 |
3 |
0.97319 |
0 |
00639 |
1.005 |
1.012 |
|
|
4 |
95409 |
0*01145 |
1*042 |
1.05S |
4 |
0.95367 |
0 |
01060 |
1.035 |
1.066 |
|
|
5 |
93022 |
0*01659 |
1*057 |
1.077 |
5 |
0.92963 |
0 |
01563 |
1.062 |
1.061 |
|
|
6 |
90185 |
0*02223 |
1*073 |
1*099 |
6 |
0.90067 |
0 |
02079 |
1.0S1 |
1.077 |
|
|
7 |
86942 |
0*02829 |
1*090 |
1*123 |
7 |
0.06763 |
0 |
02075 |
1.063 |
1.09S |
|
|
8 |
8ЭЭЭ6 |
0*03455 |
1*105 |
1*146 |
8 |
0.03062 |
0 |
03321 |
1.076 |
1.116 |
|
|
9 |
79408 |
0*04081 |
1*119 |
1*167 |
9 |
0.79010 |
0 |
06006 |
1.092 |
1.139 |
|
|
10 |
75200 |
0*04691 |
1*132 |
1*188 |
10 |
0,76727 |
9 |
06713 |
1.110 |
1,166 |
|
|
11 |
70756 |
0*05267 |
1*143 |
1*208 |
11 |
0.70230 |
0 |
05621 |
1.130 |
1.195 |
|
|
12 |
66122 |
0*05793 |
1*153 |
1*228 |
12 |
0.65560 |
0 |
06100 |
1.1S2 |
1.227 |
|
|
13 |
61344 |
0*06257 |
1*161 |
1*246 |
13 |
0.00056 |
0 |
06739 |
1.170 |
1.262 |
|
|
14 |
56469 |
0*06646 |
1*168 |
1*264 |
14 |
0.56091 |
0 |
07286 |
1.201 |
1.300 |
|
|
15 |
51543 |
0*06950 |
1*173 |
1*281 |
15 |
0.51352 |
9 |
07697 |
1.229 |
1.362 |
|
|
16 |
46615 |
0*07162 |
1*177 |
1*298 |
16 |
0.60626 |
0 |
07915 |
1.222 |
1.366 |
|
|
17 |
41731 |
0*07275 |
1 • 1179 |
1.315 |
17 |
0.61697 |
0 |
07976 |
1.215 |
1.356 |
|
|
18 |
36938 |
0*07288 |
1*180 |
1*331 |
18 |
0.37226 |
9 |
07905 |
1.206 |
1.361 |
|
|
19 |
32280 |
0.07197 |
1*178 |
1*348 |
19 |
0.32656 |
9 |
07716 |
1.197 |
1.369 |
|
|
ao |
27803 |
0*07004 |
1*175 |
1*365 |
20 |
0.26233 |
9 |
07622 |
1.165 |
1.377 |
|
|
U |
23547 |
0*06710 |
1*168 |
1*382 |
21 |
0.26007 |
9 |
07026 |
1.171 |
1.385 |
|
|
22 |
19553 |
0*06322 |
1*159 |
1.401 |
22 |
0.20017 |
9 |
06530 |
1.154 |
1.395 |
|
|
23 |
15858 |
0*05844 |
1*145 |
1*420 |
23 |
0.16305 |
9 |
05966 |
1.133 |
1.605 |
|
|
24 |
12494 |
0*05285 |
1*124 |
1*441 |
24 |
0.12905 |
9 |
05326 |
1.100 |
1.617 |
|
|
25 |
09490 |
0*04653 |
1*095 |
1*464 |
25 |
0.09651 |
9 |
06627 |
1.070 |
1.630 |
|
|
26 |
06872 |
0*03960 |
1*052 |
1*487 |
26 |
0.07170 |
9 |
03680 |
1.022 |
1.666 |
|
|
27 |
04658 |
0*03221 |
0*986 |
1*511 |
27 |
0.06660 |
9 |
03119 |
0.956 |
1.661 |
|
|
28 |
0?863 |
0*02453 |
0*861 |
1*531 |
28 |
0.03022 |
9 |
02363 |
0.652 |
1.660 |
|
|
29 |
Of 496 |
0*01680 |
0.70S |
1.543 |
29 |
0.01569 |
9 |
01563 |
0.686 |
1.502 |
|
|
30 |
0<) 560 |
0*00931 |
0*382 |
1*525 |
30 |
0.00600 |
9 |
00605 |
0.361 |
1.519 |
|
|
31 |
06056 |
0.002S8 |
0*286 |
1*429 |
31 |
0.00061 |
9 |
00261 |
0.306 |
1.519 |
|
|
32 |
00075 |
•0*00255 |
1*503 |
0.752 |
32 |
0.00079 |
•9 |
00236 |
1.506 |
0.752 |
|
|
33 |
06675 |
•0*00664 |
1*390 |
0*199 |
33 |
0.00693 |
•9 |
00629 |
1.390 |
0.199 |
|
|
34 |
01818 |
-0*01038 |
1*318 |
0.S29 |
34 |
0.01636 |
•9 |
00993 |
1.316 |
0.5Э0 |
|
|
35 |
03477 |
-0*01348 |
1*260 |
0*683 |
35 |
O. OSSOO |
-9 |
01295 |
1.260 |
0.663 |
|
|
36 |
05640 |
-0*01582 |
1*215 |
0*766 |
36 |
0.05066 |
-9 |
01522 |
1.216 |
0.766 |
|
|
37 |
08293 |
-0*01735 |
1*178 |
0*814 |
37 |
0.06317 |
-9 |
01670 |
1.178 |
0.616 |
|
|
38 |
11415 |
•0*01810 |
1*146 |
0*843 |
38 |
0.11639 |
•9 |
01761 |
1.166 |
0,663 |
|
|
39 |
14979 |
•0*01809 |
1*118 |
0*861 |
39 |
0.15006 |
•9 |
01730 |
1.116 |
0.661 |
|
|
60 |
18954 |
-0*01740 |
1*093 |
0*872 |
40 |
0.16979 |
-9 |
01006 |
1.096 |
0.673 |
|
|
41 |
23300 |
-0*01610 |
1*071 |
0!* 879 |
41 |
0.23325 |
•9 |
01533 |
1.071 |
0,679 |
|
|
42 |
27973 |
-0*01431 |
1*051 |
0*882 |
42 |
0.27990 |
•9 |
01352 |
1.05І |
0.663 |
|
|
4*% |
32924 |
-0*01212 |
1*032 |
0*884 |
43 |
0.32950 |
•9 |
01131 |
1.033 |
0.666 |
|
|
44 |
38098 |
-0*00965 |
1*01S |
0*883 |
44 |
0.36126 |
•9 |
00866 |
1.0І6 |
0.6*6 |
|
|
45 |
43439 |
-0*00701 |
0*999 |
0*882 |
45 |
0.6Э66Т |
•9 |
00021 |
0.999 |
0,6*2 |
|
|
46 |
48884 |
-0*00434 |
0*984 |
0*879 |
46 |
0.66912 |
•9 |
00356 |
0.966 |
o. tao |
|
|
47 |
54370 |
-0*00173 |
0*970 |
0*876 |
47 |
0.56399 |
-9 |
00095 |
0.970 |
0.876 |
|
|
48 |
59831 |
0*00069 |
0*956 |
0*873 |
48 |
0.59661 |
9 |
00165 |
0.956 |
0.673 |
|
|
49 |
65199 |
0*00284 |
0*943 |
0*869 |
49 |
0.05230 |
9 |
00357 |
0.963 |
0.669 |
|
|
50 |
70409 |
0*00461 |
0..9Э0 |
0*864 |
50 |
0.70660 |
9 |
00531 |
0.930 |
0.666 |
|
|
51 |
75392 |
0*00595 |
0*918 |
0*859 |
51 |
0.75626 |
9 |
00661 |
0.916 |
0.660 |
|
|
52 |
80082 |
0*00678 |
0*906 |
0*8S5 |
52 |
0.60115 |
9 |
00760 |
0.906 |
0.655 |
|
|
53 |
84416 |
0*00709 |
0*894 |
0*849 |
S3 |
0.06650 |
9 |
00705 |
0.696 |
0.650 |
|
|
54 |
88331 |
0*00686 |
0*883 |
0*844 |
54 |
0.06305 |
9 |
00730 |
0.663 |
0,666 |
|
|
55 |
91770 |
0*00612 |
0*871 |
0*839 |
55 |
0.91603 |
9 |
00656 |
0.672 |
0.639 |
|
|
56 |
94675 |
0*00491 |
0*861 |
0*833 |
56 |
0.96709 |
9 |
00522 |
0.661 |
0.636 |
|
|
57 |
96990 |
0*00333 |
0*857 |
0*83$ |
57 |
0.97019 |
9 |
00350 |
0.660 |
0.637 |
|
|
58 |
98661 |
0*00169 |
0*861 |
0*843 |
58 |
0.98660 |
9 |
00175 |
0.670 |
0.652 |
|
|
59 |
99665 |
0*00046 |
0*865 |
0*853 |
59 |
0.99071 |
9 |
00066 |
0.660 |
0.667 |
|
|
60 |
00000 |
0*00000 |
0*862 |
0*854 |
60 |
1.00000 |
9 |
00000 |
0.679 |
0.871 |
|
|
ALPHAO « |
4«SS |
DEGREES |
CMO a-0*1222 |
ALPNAt * 6.56 oegrees |
CNO >«0.1206 |
||||||
|
ETA « |
1*071 |
ETA « |
1.072 |
|
WARNING * SUBROUTINE SMOOTH HAS SLOPES WARNING – SUBROUTINE SMOOTH HAS SLOPES •0.3B0 *N0-0*482 BETWEEN POINTS 32 ANO 3 «0.406 ANO-0.691 BETWEEN POINTS 32 AND |
EPPLER 205 EPPLER 207 EPPLER 209
PROF1L E 205 10.484b PROFIL E 207 12.04% PROFIL E209 13.78%
|
N |
X |
Y |
X |
Y |
X |
Y |
|
0 |
100.000 |
0.000 |
100.000 |
0.000 |
100.000 |
0.000 |
|
1 |
99.655 |
.039 |
99.647 |
.045 |
99.639 |
.052 |
|
2 |
98.649 |
.174 |
98.625 |
.202 |
98.600 |
.232 |
|
3 |
97.049 |
.427 |
97.011 |
.489 |
96.969 |
.557 |
|
4 |
94.916 |
.778 |
94.870 |
.881 |
94.821 |
.992 |
|
5 |
92.285 |
1.196 |
92.238 |
1.337 |
92.187 |
1.488 |
|
6 |
89.175 |
1.668 |
89.128 |
1.841 |
89.077 |
2.027 |
|
7 |
85.624 |
2.199 |
85.576 |
2.400 |
85.523 |
2.615 |
|
8 |
81.684 |
2.786 |
81.633 |
3.011 |
81.577 |
3.253 |
|
9 |
77.412 |
3.419 |
77.357 |
3.666 |
77.295 |
3.930 |
|
10 |
72.866 |
4.088 |
72.806 |
4.352 |
72.738 |
4.634 |
|
11 |
68.108 |
4.777 |
68.043 |
5.055 |
67.968 |
5.352 |
|
12 |
63.204 |
5.470 |
63.132 |
5.759 |
63.049 |
6.065 |
|
13 |
58.218 |
6.147 |
58.139 |
6.441 |
58.047 |
6.753 |
|
14 |
53.217 |
6.782 |
53.129 |
7.079 |
53.028 |
7.393 |
|
15 |
48.265 |
7.342 |
48.169 |
7.638 |
48.058 |
7.949 |
|
16 |
43.410 |
7.785 |
43.306 |
8.075 |
43.185 |
8.380 |
|
17 |
38.680 |
8.081 |
38.567 |
8.362 |
38.436 |
8.657 |
|
18 |
34.101 |
8.214 |
33.981 |
8.483 |
33.841 |
8.764 |
|
19 |
29.699 |
8.177 |
29.573 |
8.430 |
29.424 |
8.694 |
|
20 |
25.496 |
7.970 |
25.363 |
8.205 |
25.208 |
8.448 |
|
21 |
21.508 |
7.606 |
21.371 |
7.819 |
21.211 |
8.037 |
|
22 |
17.764 |
7.111 |
17.626 |
7.300 |
17.461 |
7.490 |
|
23 |
14.302 |
6.507 |
14.162 |
6.669 |
13.997 |
6.830 |
|
24 |
11.157 |
5.811 |
11.018 |
5.944 |
10.854 |
6.073 |
|
25 |
8.360 |
5.040 |
8.225 |
5.143 |
8.065 |
5.237 |
|
26 |
5.937 |
4.211 |
5.808 |
4.282 |
5.656 |
4.341 |
|
27 |
3.909 |
3.344 |
3.791 |
3.383 |
3.651 |
3.406 |
|
28 |
2.292 |
2.461 |
2.189 |
2.468 |
2.066 |
2.454 |
|
29 |
1.097 |
1.589 |
1.015 |
1.565 |
.916 |
1.517 |
|
30 |
.331 |
.766 |
.279 |
.714 |
.216 |
.635 |
|
31 |
.002 |
.055 |
.000 |
-.015 |
.007 |
-.106 |
|
32 |
.233 |
-.506 |
.304 |
-.626 |
.398 |
-.775 |
|
33 |
1.065 |
-.988 |
1.212 |
-1.204 |
1.379 |
-1.467 |
|
34 |
2.419 |
-1.420 |
2.628 |
-1.750 |
2.852 |
-2.140 |
|
35 |
4.291 |
-1.776 |
4.543 |
-2.234 |
4.804 |
-2.765 |
|
36 |
6.669 |
-2.053 |
6.943 |
-2.649 |
7.219 |
-3.329 |
|
37 |
9.534 |
-2.252 |
9.807 |
-2.991 |
10.073 |
-3.821 |
|
38 |
12.864 |
-2.378 |
13.109 |
-3.257 |
13.340 |
-4.233 |
|
39 |
16.627 |
-2.436 |
16.817 |
-3.448 |
16.986 |
-4.561 |
|
40 |
20.783 |
-2.435 |
20.893 |
-565 |
20.974 |
-4.799 |
|
41 |
25.290 |
-2.384 |
25.292 |
-3.611 |
25.258 |
-4.943 |
|
42 |
30.097 |
-2.292 |
29.966 |
-3.586 |
29.793 |
-4.985 |
|
43 |
35.149 |
-2.168 |
34.861 |
-3.487 |
34.524 |
-4.909 |
|
44 |
40.388 |
-2.021 |
39.937 |
-3.302 |
39.430 |
-4.683 |
|
45 |
45.751 |
-1.859 |
45.165 |
-3.044 |
44.516 |
-4.322 |
|
46 |
51.174 |
-1.689 |
50.495 |
-2.744 |
49.749 |
-3.884 |
|
47 |
56.591 |
-1.516 |
55.860 |
-2.425 |
55.057 |
-3.409 |
|
48 |
61.938 |
-1.345 |
61.189 |
-2.102 |
60.368 |
-2.923 |
|
49 |
67.149 |
-1.180 |
66.414 |
-1.787 |
65.609 |
-2.446 |
|
50 |
72.160 |
-1.023 |
71.467 |
-1.488 |
70.708 |
-1.993 |
|
51 |
76.911 |
-.876 |
76.283 |
-1.212 |
75.594 |
-1.576 |
|
52 |
81.343 |
-.740 |
80.796 |
-.963 |
80.197 |
-1.205 |
|
53 |
85.400 |
-.614 |
84.948 |
-.744 |
84.451 |
-.884 |
|
54 |
89.034 |
-.380 |
91.942 |
-.390 |
91.665 |
-.400 |
|
55 |
92.195 |
-.380 |
91.942 |
-.390 |
91.665 |
-.400 |
|
56 |
94.860 |
-.252 |
94.699 |
-.239 |
94.522 |
-.222 |
|
57 |
97.017 |
-.125 |
96.930 |
-.108 |
96.834 |
-.089 |
|
58 |
98.635 |
-.036 |
98.598 |
-.026 |
98.558 |
-.014 |
|
59 |
99.651 |
-.003 |
99.643 |
-.000 |
99.633 |
.003 |
|
60 |
100.000 |
.000 |
100.000 |
.000 |
100.000 |
-.000 |
|
CM = |
-.0460 fi « |
2.37° |
CM = -.0499 fi |
= 2.33е |
CM * -.0547 fi |
= 2.28° |
|
XU |
YU |
|
.000 |
900 |
|
.026 |
.190 |
|
.466 |
.915 |
|
1.344 |
1.740 |
|
2.652 |
2906 |
|
4.363 |
3.487 |
|
6.525 |
4.352 |
|
9.061 |
5.161 |
|
11.957 |
5.957 |
|
15.218 |
5.663 |
|
19780 |
7.284 |
|
22920 |
7905 |
|
26.595 |
6.213 |
|
30.967 |
8.487 |
|
39403 |
8.603 |
|
39.979 |
8951 |
|
44973 |
8.332 |
|
49.458 |
7.954 |
|
54.305 |
7.438 |
|
59.186 |
8908 |
|
64.052 |
8.112 |
|
56939 |
6.381 |
|
73.484 |
4.842 |
|
77.923 |
3.914 |
|
82.096 |
3.214 |
|
85.945 |
2.558 |
|
89.414 |
1957 |
|
92.452 |
1.415 |
|
95.023 |
932 |
|
97.106 |
.522 |
|
98.674 |
.220 |
|
99.661 |
.051 |
|
100.000 |
.000 |
XL YL.000 000 .129 -.375 919 -.938 2.044 -1.252 3.791 -1.598 6.049 -1841 8901 -2.010 12.026 -2.098 15.697 -2.112 19.778 -2.061 24.227 -1.955 28.998 -1.807 34.035 -1.628 39.280 -1.430 44.672 -1.244 50.145 -1.019 55.630 – 824 61.059 -.645 66.384 -.486 71.479 -950 76.339 -.239 80982 -.153 85.050 -.091 88.788 -.048 92.048 -.018 94.794 .010
97.003 .032
98.640 .034
99.655 .014
100.000 .000
|
Wortmann FX 38*153 Camber 2.1 fercant |
|
AIRFOIL |
0008 10 |
.80X |
AIRFOIL |
12 |
9.27X |
AIRFOIL 14 |
8.47X |
|||
|
N |
X |
Y |
N |
К |
Y |
N |
X |
Y |
||
|
0 |
100.000 |
0. |
0 |
0 |
100. |
.000 |
0.0 |
0 |
100.000 |
0.0 |
|
1 |
99.664 |
0. |
082 |
1 |
99. |
.665 |
0.052 |
1 |
99.667 |
0.045 |
|
2 |
98.714 |
0. |
338 |
2 |
98. |
.701 |
0.219 |
2 |
98.707 |
0.195 |
|
3 |
97.253 |
0. |
740 |
3 |
97, |
.190 |
0.497 |
3 |
97.194 |
0.446 |
|
4 |
95.321 |
1. |
211 |
4 |
95 |
.174 |
0 .837 |
4 |
95.169 |
0.760 |
|
5 |
92.908 |
1. |
712 |
5 |
92 |
.660 |
1.213 |
5 |
92.645 |
1.112 |
|
6 |
90.028 |
2. |
250 |
6 |
89 |
.671 |
1.629 |
6 |
89.647 |
1.506 |
|
7 |
86.722 |
2. |
819 |
7 |
86. |
.251 |
2.080 |
7 |
86.218 |
1.937 |
|
8 |
83.033 |
3. |
407 |
8 |
82 |
.447 |
2.557 |
8 |
82.405 |
2.394 |
|
9 |
79.007 |
4. |
001 |
9 |
78 |
.304 |
3.047 |
9 |
78.255 |
2.867 |
|
10 |
74.689 |
4. |
586 |
10 |
73 |
.875 |
3.538 |
10 |
73.817 |
3.344 |
|
11 |
70.131 |
5. |
147 |
11 |
69 |
.209 |
4.018 |
11 |
69.145 |
3.811 |
|
12 |
65.381 |
5. |
672 |
12 |
64 |
.361 |
4.472 |
12 |
64.292 |
4.256 |
|
13 |
60.492 |
6. |
147 |
13 |
59 |
. 384 |
4.889 |
13 |
59.310 |
4.666 |
|
14 |
55.516 |
6. |
558 |
14 |
54 |
.331 |
5.256 |
14 |
54.254 |
5.029 |
|
15 |
50.504 |
6. |
895 |
15 |
49 |
.257 |
5.562 |
15 |
49.178 |
5.334 |
|
16 |
45.508 |
7. |
146 |
16 |
44 |
.213 |
5.795 |
16 |
44.133 |
5.570 |
|
17 |
40.577 |
7. |
303 |
17 |
39 |
.251 |
5.948 |
17 |
39.172 |
5.727 |
|
18 |
35.760 |
7. |
359 |
18 |
34 |
.419 |
6.013 |
18 |
34.343 |
5.800 |
|
19 |
31.103 |
7. |
309 |
19 |
29 |
. 765 |
5.984 |
19 |
29.692 |
5.780 |
|
20 |
26.649 |
7. |
149 |
20 |
25 |
.331 |
5.857 |
20 |
25.262 |
5.666. |
|
21 |
22.440 |
6. |
878 |
21 |
21 |
.158 |
5.631 |
21 |
21.095 |
5.456i |
|
22 |
18.512 |
6. |
498 |
22 |
17 |
.282 |
5.308 |
22 |
17.226 |
5.151 |
|
23 |
14.898 |
6. |
013 |
23 |
13 |
.>36 |
4.892 |
23 |
13.689 |
4.755 |
|
24 |
11.627 |
5. |
431 |
24 |
10 |
.551 |
4.391 |
24 |
10.513 |
4.275 |
|
25 |
8.724 |
4. |
763 |
25 |
7 |
.750 |
3.815 |
25 |
7.725 |
3.721 |
|
26 |
6.211 |
4. |
023 |
26 |
5 |
.357 |
3.176 |
26 |
5.344 |
3.104 |
|
27 |
4.105 |
3. |
230 |
27 |
3 |
.389 |
2.492 |
27 |
3.388 |
2.439 |
|
28 |
2.421 |
2. |
405 |
28 |
1 |
.859 |
1.779 |
28 |
1.867 |
1.744 |
|
29 |
1.169 |
1. |
577 |
29 |
0 |
.772 |
1.067 |
29 |
0.786 |
1.048 |
|
30 |
0.360 |
0. |
779 |
30 |
0 |
.140 |
0.393 |
30 |
0.150 |
0.390 |
|
31 |
0.004 |
0. |
079 |
31 |
0. |
.026 |
-0.161 |
31 |
0.022 |
-0.139 |
|
32 |
0.219 |
-0. |
521 |
32 |
0. |
.486 |
-0.652 |
32 |
0.465 |
-0.595 |
|
33 |
1.024 |
-1. |
097 |
33 |
1 |
.483 |
-1.155 |
33 |
1.447 |
-1.055 |
|
34 |
2.328 |
-1. |
645 |
34 |
2 |
.985 |
-1.618 |
34 |
2.938 |
-1.468 |
|
35 |
4.124 |
-2. |
137 |
35 |
4 |
.983 |
-2.030 |
35 |
4.931 |
-1.824 |
|
36 |
6.398 |
*2. |
559 |
36 |
7 |
.462 |
-2.382 |
36 |
7.412 |
-2.116 |
|
37 |
9.136 |
-2. |
903 |
37 |
10 |
.404 |
-2.673 |
37 |
10.363 |
-2.346 |
|
38 |
12.318 |
-3. |
170 |
38 |
13 |
.781 |
-2.903 |
38 |
13.756 |
-2.515 |
|
39 |
15.914 |
•3. |
363 |
39 |
17 |
.558 |
-3.074 |
39 |
17.559 |
-2.629 |
|
40 |
19.884 |
-3. |
484 |
40 |
21 |
.697 |
-3.190 |
40 |
21.730 |
-2.690 |
|
41 |
24.185 |
-3. |
538 |
41 |
26, |
.153 |
-3.252 |
41 |
26.227 |
-2.705 |
|
42 |
28.769 |
-3. |
525 |
42 |
30. |
.876 |
-3.266 |
42 |
30.998 |
-2.680 |
|
43 |
33.580 |
-3. |
.446 |
43 |
35. |
.813 |
-3.235 |
43 |
35.989 |
-2.619 |
|
44 |
38.562 |
-3. |
.299 |
44 |
40. |
.907 |
-3.161 |
44 |
41.144 |
-2.527 |
|
45 |
43.655 |
-3. |
.069 |
45 |
46. |
.098 |
-3.046 |
45 |
46.401 |
-2.409 |
|
46 |
48.825 |
-2. |
.728 |
46 |
51. |
.327 |
-2.891 |
46 |
51.701 |
-2.267 |
|
47 |
54.071 |
-2. |
.287 |
47 |
56. |
.530 |
-2.694 |
47 |
56.979 |
-2.105 |
|
48 |
59.361 |
-1. |
.802 |
48 |
61. |
.646 |
-2.448 |
48 |
62.175 |
-1.921 |
|
49 |
64.626 |
►1. |
.317 |
49 |
66. |
.629 |
-2.128 |
49 |
67.227 |
-1.718 |
|
50 |
69.792 |
-0, |
.862 |
50 |
71. |
.476 |
-1.732 |
50 |
72.073 |
-1.480 |
|
51 |
74.784 |
-0. |
.463 |
51 |
76. |
.164 |
-1.318 |
51 |
76.689 |
-1.194 |
|
52 |
79.524 |
-0. |
.138 |
52 |
80. |
.621 |
-0.934 |
52 |
81.057 |
-0.890 |
|
53 |
83.934 |
0. |
.102 |
53 |
84. |
.773 |
-0.604 |
53 |
85.121 |
-0.612 |
|
54 |
87.940 |
0. |
.252 |
54 |
88. |
.550 |
-0.342 |
54 |
88.811 |
-0.382 |
|
55 |
91.469 |
0. |
.315 |
55 |
91. |
.881 |
-0.155 |
55 |
92.063 |
-0.209 |
|
56 |
94.456 |
0. |
.302 |
56 |
94. |
705 |
-0.039 |
56 |
94.817 |
-0.091 |
|
57 |
96.845 |
0. |
.233 |
57 |
96. |
.969 |
0.020 |
57 |
97.026 |
-0.019 |
|
58 |
98.586 |
0. |
.133 |
58 |
98. |
‘632 |
0.032 |
58 |
98.654 |
0.012 |
|
59 |
99.645 |
0. |
.040 |
59 |
99. |
654 |
0.014 |
59 |
99.659 |
0.008 |
|
60 |
100.000 |
0. |
.000 |
60 |
160. |
000 |
0.0 |
60 |
100.000 |
0.0 |
|
ALPHAO CMO = – |
= 3.74 DEGREES 0.1028 |
ALPHAO cno |
s 2. =-0. |
07 0527 |
DEGREES |
ALPHAO cno |
и и i Є N* ** V» |
DEGREES |
|
JANOVEC 8*12 |
|
888*388**38 |
x у
|
1 . иисюи |
U. UUU1M |
|
.99674 |
.00039 |
|
.99707 |
.00150 |
|
.97126 |
.00367 |
|
.94970 |
.00699 |
|
.92292 |
.01150 |
|
.69147 |
.01713 |
|
.69594 |
.02373 |
|
.6169Э |
.03107 |
|
.77501 |
.03666 |
|
.73070 |
.04669 |
|
.66454 |
.05479 |
|
.63700 |
.06231 |
|
.96656 |
.06920 |
|
.53965 |
.07526 |
|
.49073 |
.06029 |
|
.44220 |
.06416 |
|
.39450 |
.06677 |
|
.34605 |
.06605 |
|
.30323 |
.06794 |
|
.26043 |
.06644 |
|
.22002 |
.06356 |
|
.16232 |
.07934 |
|
.14769 |
.07362 |
|
.11622 |
.06706 |
|
.06623 |
.05927 |
|
.06364 |
.05060 |
|
.04320 |
.04130 |
|
.02649 |
.03166 |
|
. 01374 |
.02205 |
|
.00517 |
.01269 |
|
.00077 |
.00401 |
|
.00056 |
*.00312 |
|
.00579 |
*.00664 |
|
.01662 |
-.01315 |
|
.03263 |
-.01645 |
|
.05397 |
-.01644 |
|
.06063 |
-.01936 |
|
.11236 |
-.01939 |
|
.14663 |
-.01673 |
|
.16960 |
-.01750 |
|
.23417 |
-.01561 |
|
.26205 |
-.01374 |
|
.33271 |
-.01142 |
|
.36555 |
-.00694 |
|
.43995 |
-.00643 |
|
.49526 |
•.00396 |
|
.99066 |
-.00171 |
|
.60605 |
.00029 |
|
.66009 |
.00162 |
|
.71216 |
.00296 |
|
.76166 |
.00367 |
|
.60795 |
.00397 |
|
.65036 |
.00391 |
|
.66634 |
.00354 |
|
.92140 |
.00299 |
|
.94911 |
.00222 |
|
.67109 |
.00144 |
|
.96709 |
.00073 |
|
.99674 |
.00020 |
|
1.00000 |
-.00000 |
|
X |
У |
X |
У |
X |
У |
X |
У |
|
00000 |
0.00000 |
1.00000 |
0.00000 |
1.Ос000 |
0.00000 |
1.00000 |
0.ооооо |
|
99679 |
.00126 |
.99662 |
.00093 |
.99679 |
.00034 |
.99677 |
.00099 |
|
96799 |
.00901 |
.96666 |
.00231 |
.96709 |
.00147 |
.96736 |
.00226 |
|
97456 |
.01036 |
.97193 |
.00936 |
.97129 |
.00363 |
.97242 |
.00921 |
|
99696 |
.01636 |
.99119 |
.00939 |
.94976 |
.00696 |
.99237 |
.00906 |
|
93361 |
.02299 |
.92601 |
.01361 |
.92304 |
.*01 199 |
.92746 |
.01399 |
|
90692 |
.03009 |
.69611 |
.01677 |
.69170 |
.01729 |
.69794 |
.01666 |
|
67910 |
.03766 |
.86192 |
.021*22 |
.69637 |
.02403 |
.66424 |
.02430 |
|
63996 |
.04997 |
.62393 |
.03011 |
.61764 |
.03191 |
.82669 |
.03033 |
|
60196 |
.09396 |
.76266 |
.03632 |
.77610 |
.03949 |
.76630 |
.03697 |
|
76043 |
.06192 |
.73669 |
.04271 |
.73227 |
.04792 |
.74310 |
.04262 |
|
71703 |
.06914 |
.69260 |
.04911 |
.66669 |
.09941 |
.69771 |
.04663 |
|
67169 |
.07619 |
.64900 |
.09931 |
.63971 |
.06283 |
.69062 |
.09439 |
|
62932 |
.06241 |
.99647 |
.06102 |
.99169 |
.06990 |
.60229 |
.09934 |
|
97762 |
.06760 |
.94793 |
.06992 |
.94399 |
.07320 |
.99306 |
.06392 |
|
92979 |
.09167 |
.49693 |
.06973 |
.49922 |
.07974 |
.90349 |
.06663 |
|
46196 |
.09493 |
.44977 |
.07232 |
.44716 |
.06302 |
.49401 |
.06922 |
|
43371 |
.09606 |
.40160 |
.07366 |
.39979 |
.06492 |
.40907 |
.07062 |
|
38660 |
.09626 |
.39444 |
.07363 |
.39346 |
.06943 |
.39714 |
.07102 |
|
34064 |
.09912 |
.30666 |
.07280 |
.30862 |
.06494 |
.31066 |
.07042 |
|
29623 |
.09296 |
.26476 |
.07066 |
.26999 |
.06226 |
.26612 |
.06669 |
|
29373 |
.06671 |
.22310 |
.06749 |
.22460 |
.07676 |
.22394 |
.06631 |
|
21390 |
.06361 |
.16409 |
.06333 |
. 6620 |
.07414 |
.18493 |
.06269 |
|
17967 |
.07741 |
.14613 |
.09626 |
.19074 |
.06649 |
.14630 |
.09649 |
|
14120 |
.07023 |
.11991 |
.09243 |
.11699 |
.06166 |
.11999 |
.09326 |
|
10960 |
.06229 |
.06699 |
.04966 |
.06966 |
.09436 |
.06699 |
.04729 |
|
06196 |
.09361 |
.06147 |
.03679 |
.06493 |
.04617 |
.06167 |
.04060 |
|
09792 |
.04491 |
.04093 |
.03131 |
.04366 |
.03741 |
.04093 |
03323 |
|
03769 |
.03919 |
.02366 |
.02360 |
.02677 |
.02839 |
.02437 |
.02936 |
|
02206 |
.02979 |
.01163 |
.01964 |
.01380 |
.01936 |
.01204 |
.01730 |
|
01090 |
.01649 |
.00377 |
.00623 |
.00903 |
.01069 |
.00400 |
.00939 |
|
00313 |
.00776 |
.00013 |
.00131 |
.00046 |
.00263 |
.00021 |
.00191 |
|
00001 |
.00038 |
.00192 |
-.00392 |
.00079 |
•.00320 |
.00119 |
-.00406 |
|
00246 |
-.00902 |
.00676 |
-.00761 |
.00681 |
-.00767 |
.00799 |
•.00692 |
|
01117 |
•.00919 |
.02169 |
-.01116 |
.01639 |
-.01209 |
.01909 |
-.01317 |
|
02993 |
-.01267 |
.03990 |
-.01368 |
.03499 |
-.01946 |
.03994 |
-.01630 |
|
04922 |
-.01994 |
.06334 |
-.01992 |
.09666 |
-.01760 |
.09723 |
-.01620 |
|
07000 |
-.01634 |
.09177 |
-.01729 |
.06326 |
-.01906 |
.06413 |
-.01911 |
|
09999 |
•.02006 |
.12494 |
-.01606 |
.11474 |
-.01932 |
. 1999 |
-.01920 |
|
13368 |
-.02111 |
.16249 |
-.01640 |
.19069 |
-.01669 |
.19247 |
-.01669 |
|
17169 |
-.02192 |
.20391 |
-.01629 |
.19129 |
-.01724 |
.19313 |
-.01797 |
|
21376 |
-.02129 |
.24679 |
-.01771 |
.23969 |
-.01926 |
.23791 |
-.01609 |
|
29666 |
•.02044 |
.29*61 |
-.01671 |
.26349 |
-.01292 |
.26909 |
-.01417 |
|
30669 |
-.01697 |
.34696 |
-.01941 |
.33413 |
-.01034 |
.33937 |
-.01202 |
|
39670 |
-.01689 |
.39927 |
-.01392 |
.36706 |
-.00772 |
.36774 |
-.00970 |
|
40636 |
-.01409 |
..49266 |
-.01231 |
.44199 |
-. 009,16 |
.44162 |
•.00726 |
|
46124 |
-.01061 |
.90711 |
-.01064 |
.49702 |
•.00279 |
.49640 |
-.00467 |
|
91493 |
-.00639 |
.96136 |
•.00696 |
.99269 |
•.00069 |
.99149 |
•.00296 |
|
96931 |
-.00192 |
.61907 |
-.00731 |
.60776 |
.00107 |
.60606 |
•.00093 |
|
62394 |
.00324 |
.66792 |
’-. 00979 |
.66163 |
.00249 |
.69997 |
.00121 |
|
67603 |
.00747 |
.71609 |
-.00443 |
.71396 |
.00342 |
.71127 |
.00260 |
|
73071 |
.0.1064 |
.76614 |
•.00326 |
.76267 |
.00400 |
.76091 |
.00360 |
|
76110 |
.01311 |
.61109 |
•.00236 |
.60693 |
.00420 |
.60669 |
.00416 |
|
62629 |
.01419 |
.69226 |
-.00169 |
.69114 |
.00406 |
.64906 |
.00436 |
|
87139 |
.01390 |
.68923 |
-.00113 |
.66693 |
.00364 |
.66717 |
.00416 |
|
90999 |
.01242 |
.92149 |
•.00079 |
.92163 |
.00301 |
.92046 |
.00363 |
|
94190 |
.00962 |
.94694 |
-.00041 |
.94939 |
.00229 |
.94643 |
.00269 |
|
96749 |
.00646 |
.97026 |
-.00003 |
.97126 |
.00146 |
.97066 |
.00193 |
|
96969 |
.00321 |
.96646 |
.00016 |
.96713 |
.00074 |
.96666 |
.00102 |
|
99649 |
.00069 |
.99699 |
.00010 |
.99677 |
.00020 |
.99670 |
.00029 |
|
006oo |
.OCOOO |
1*00046 |
•40000 |
1 • 00006 |
,йОлло |
І. ОоООО |
• 04000 |
|
X |
У |
X |
У |
X |
У |
X |
У |
|
00000 |
0.00000 |
1.ooooo |
0.00000 |
1.оооос |
0.00000 |
1.00000 |
0.00000 |
|
99694 |
.00023 |
.99694 |
.00036 |
.99690 |
.00042 |
.99669 |
.00043 |
|
96621 |
.00111 |
.99746 |
.00196 |
.99619 |
.00196 |
.99679 |
.00194 |
|
96929 |
.00307 |
.97209 |
.00376 |
.96949 |
.00461 |
.97069 |
.00444 |
|
94604 |
.*00694 |
.99106 |
.00702 |
.94697 |
.00991 |
.94993 |
.00834 |
|
91742 |
.01192 |
.92493 |
.01132 |
.91927 |
.01444 |
.92202 |
.01391 |
|
•6429 |
.01990 |
.99394 |
.01661 |
.99703 |
.02139 |
.99094 |
.01994 |
|
94791 |
.02797 |
.99961 |
.02279 |
.99099 |
.02939 |
.99907 |
.02714 |
|
90901 |
.03749 |
.91971 |
.02971 |
.91146 |
.03917 |
.91616 |
.03916 |
|
76666 |
.04799 |
.77769 |
.03719 |
.76933 |
.04740 |
.77439 |
.04369 |
|
72424 |
.09930 |
.73313 |
.04497 |
.72903 |
.09674 |
.73029 |
.09230 |
|
9909Э |
.06722 |
.69661 |
.09290 |
.67907 |
.06996 |
.69439 |
.06064 |
|
63993 |
.07442 |
.63999 |
.06042 |
.63196 |
.07443 |
.63721 |
.06996 |
|
99999 |
.06029 |
.99961 |
.06762 |
.99414 |
.09219 |
.99923 |
.07640 |
|
94234 |
.09492 |
.94019 |
.07420 |
.93609 |
.09991 |
.94091 |
.08299 |
|
49464 |
.06909 |
.49093 |
.07997 |
.49920 |
.09406 |
.49269 |
.08606 |
|
44690 |
.09996 |
.44204 |
.09472 |
.44079 |
.09770 |
.44477 |
.09187 |
|
39997 |
.09097 |
.39427 |
.09929 |
.39411 |
.09969 |
.39761 |
.09421 |
|
39312 |
.09992 |
.34799 |
.09090 |
.34997 |
.10001 |
.39194 |
.09904 |
|
.30909 |
.09904 |
.30399 |
.09119 |
.30490 |
.09667 |
.30694 |
.09439 |
|
29499 |
.09496 |
.26126 |
.09019 |
.26227 |
.09971 |
.26416 |
.09231 |
|
22379 |
.09044 |
.22127 |
.09791 |
.22219 |
.09119 |
.22361 |
.06809 |
|
19912 |
.07499 |
.19393 |
.09329 |
.19497 |
.09923 |
.16969 |
.06419 |
|
.14939 |
.06997 |
.14916 |
.07770 |
.14971 |
.07799 |
.19073 |
.07922 |
|
.11693 |
.06137 |
.11797 |
.07099 |
.11799 |
.06963 |
. 1999 |
.07113 |
|
09909 |
.09342 |
.09939 |
.06323 |
.09939 |
.06040 |
.09072 |
.06303 |
|
.09297 |
.04494 |
.06476 |
.09469 |
.06437 |
.09096 |
.06611 |
.Q9406 |
|
.04177 |
.03994 |
.04399 |
.04993 |
.04320 |
.04033 |
.04930 |
.04443 |
|
.02474 |
.02697 |
.02726 |
.03996 |
.02602 |
.03000 |
.02940 |
.03437 |
|
.01209 |
.01914 |
.01467 |
.02606 |
.01301 |
.01997 |
.01946 |
.02416 |
|
.00392 |
.00969 |
.00607 |
.01606 |
.00433 |
.01032 |
.00643 |
.01419 |
|
00019 |
.00199 |
.00129 |
.00643 |
.00017 |
.00193 |
.00130 |
.00909 |
|
00127 |
•.00429 |
.00016 |
•.00200 |
.00196 |
-.00466 |
.00030 |
-.00210 |
|
00901 |
-.00994 |
.00377 |
-.00914 |
.00916 |
-.01099 |
.00499 |
-.00721 |
|
.02093 |
•.01294 |
.01306 |
•.01234 |
.02237 |
-.01621 |
.01603 |
-.01117 |
|
0394S |
•.01613 |
.02779 |
-.01923 |
.04069 |
•.02144 |
.03260 |
-.01434 |
|
.06167 |
•.01949 |
.04791 |
-.01670 |
■ .06399 |
•.02609 |
.09491 |
-.01664 |
|
09001 |
•.02012 |
.07391 |
-.01690 |
.09171 |
•.03004 |
.06196 |
-.01907 |
|
12317 |
•.02113 |
.10493 |
-.01964 |
.12392 |
-.03322 |
.11392 |
-.01669 |
|
.16079 |
•.02160 |
.14069 |
-.01417 |
.16019 |
-.03999 |
.19011 |
-.01897 |
|
20229 |
•.02199 |
.16140 |
-.01202 |
.20012 |
-.03714 |
.19099 |
-.01764 |
|
24730 |
-.02109 |
.22624 |
-.00997 |
.24337 |
•.03762 |
.23962 |
-.01661 |
|
29934 |
-.02016 |
.27499 |
•.00696 |
.29990 |
-.03766 |
.29362 |
-.01903 |
|
.34990 |
-.01999 |
.32999 |
-.00433 |
.*33902 |
•.03672 |
.33437 |
-.01323 |
|
39639 |
-.01739 |
.37936 |
-.00176 |
.39946 |
-.03497 |
.39726 |
-.01133 |
|
49219 |
-.01969 |
.43UM9 |
.00060 |
.44031 |
-.03249 |
.44162 |
-.00942 |
|
90667 |
-.01399 |
.49043 |
.00273 |
.49309 |
-.02934 |
.49677 |
-.00799 |
|
96120 |
-.01202 |
.94699 |
.00499 |
.94629 |
-.02999 |
.89203 |
-.00999 |
|
61911 |
-.01022 |
.60221 |
.00601 |
.99939 |
-.02139 |
.60671 |
-.00429 |
|
66779 |
•.00992 |
.69660 |
.00709 |
.69199 |
-.07703 |
.66013 |
-.00291 |
|
71949 |
-.00696 |
.70909 |
.00774 |
.70341 |
-.01296 |
.71162 |
-.00179 |
|
76666 |
•;00996 |
.79997 |
.00900 |
.79299 |
-.00910 |
.76093 |
-.00079 |
|
61169 |
-.00437 |
.60964 |
.00796 |
.*79966 |
-.00991 |
.80627 |
.00001 |
|
69297 |
•.00337 |
.64947 |
.00739 |
.64299 |
-.00337 |
.94833 |
.00067 |
|
99999 |
•.00297 |
.69692 |
.00692 |
.99219 |
-.00149 |
.66622 |
.00114 |
|
92229 |
-.00193 |
.92046 |
.00946 |
.91664 |
-.00026 |
.91946 |
.00139 |
|
94931 |
-.00140 |
.94962 |
.00407 |
.94976 |
.0004^ |
.94797 |
.00137 |
|
97093 |
•.00097 |
.97093 |
.00262 |
.96909 |
.00099 |
.97009 |
.00110 |
|
99669 |
•.00039 |
.99703 |
.00131 |
.99609 |
.00043 |
.96699 |
.00069 |
|
99699 |
-.00009 |
.99674 |
.00039 |
.99649 |
.00014 |
.99661 |
.00020 |
|
OOO0O |
фОСООО |
1.00090 |
.ООбо* |
|.90 000 |
•Од ООО |
. воем |
.00ооо |
|
49 0.66752 -.0.01108 50 0.7)001 *0.01000 51 0.71171 *0.00000 52 0.02490 *0.00705 5) 0.00900 *0.00072 54 0.09707 *0.00557 55 0.92707 >0.00440 SO 0.95270 *0.00917 57 0.97279 *0.00108 50 0.90709 *0.00079 59 0.99000 – O. OGOIO 00 1.00001 *0.00000 ALPHAO – 0.02 DECREES CMO • 0.0004 |
AIRFOIL SSOlO-Rt К X Y
0 1.00000 0.0
1 0.99674 0.00001
2 0.90707 0.00007
9 0.9710] 0.000jo
4 0.94070 0.00108
5 0.92041 0.00256
6 0.00667 0.00516
7 0.04820 0.00903
0 0.80600 0.01406
9 0.76076 0.02000
10 0.71907 0.02600
11 0.66377 0.09420
12 0.61355 0.04163
19 0.56296 0.04077
14 0.51247 0.05529
15 0.46251 0.06099
16 0.41940 0.06546
17 0.96576 0.06879
10 0.91969 0.07069
19 0.27560 0.07113
20 0.23303 0.07023
21 0.19473 0.06799
22 0.15060 0.06445
29 0.12579 0.05960
24 0.09697 0.03377
25 0.07071 0.04600
26 0.04009 0.09915
27 0.03102 0.03001
20 0.01710 0.02214
29 0.00799 0.01940
90 0.00167 0.00533
91 0.00015 -0.00140
92 0.00424 *0.00650
33 0.01456 *0.01004
94 0.09020 *0.01471
95 0.05129 *0.01004
36 0.07710 *0.02002
37 0.I070S -0.02906
30 0.14291 -0.02401
39 0.10194 -0.02609
40 0.22440 -0.02600
41 0.27000 *0.02715
42 0.91029 *0.02691
43 0.96064 -0.02629
44 0.42035 -0.02517
45 0.47345 -0.02301
46 .0.52673 -0.02219
47 0.37983 -0.02039
40 0.69209 *0.01046
49 0.60292 *0.01645
50 0.73179 -0.01449
51 0.77792 -0.01243
52 0.82095 -0.01049
59 0.06090 -0.00065
54 0.09547 -0.00691
55 0.92603 *0.0052′
56 0.95163 *0.00967
57 0.97211 -0.00212
58 0.90790 -0.00000
59 0.99670 -0.00019
40 1.00001 -0.00000
ЛГ. РКАО «0.64 DECREES
CMO * 0.0006
|
X(i) |
Yo |
Yu |
X(i ) |
Yo |
Yu |
||
|
1 |
0.0000 1 |
0.OOUO |
0.0000 |
1 |
0.0000 |
0.0000 |
0.0000 |
|
г |
.0050 |
.0076 |
-.0054 |
2 |
. 0050 |
. 0084 |
-.0062 |
|
3 |
.0125 |
.0115 |
-.0088 |
3 |
.0125 |
. 0128 |
-.0101 |
|
4 |
.0250 |
.0177 |
-.0128 |
4 |
.0250 |
.0195 |
-.0147 |
|
5 |
.0500 |
.0253 |
-.0175 |
5 |
.0500 |
.0280 |
-.0202 |
|
6 |
.1000 |
.0349 |
-.0229 |
6 |
.1000 |
. 0385 |
-.0265 |
|
7 |
.1500 |
.0414 |
-.0266 |
7 |
.1500 |
. 0456 |
-.0309 |
|
8 |
.2000 |
.0448 |
-.0284 |
8 |
.2000 |
. 0494 |
-.0325 |
|
9 |
.2500 |
. 0473 |
-.0297 |
9 |
.2500 |
.0521 |
-.0345 |
|
10 |
.3000 |
.0488 |
-.0302 |
10 |
.3000 |
.0537 |
-.0351 |
|
11 |
.3500 |
. 04V6 |
-.0304 |
11 |
.3500 |
. 0546 |
-.0354 |
|
12 |
.4000 |
. 0490 |
-.0295 |
12 |
.4009 |
. 0540 |
-.0344 |
|
13 |
.5000 |
. 0463 |
-.0263 |
13 |
.5000 |
.0508 |
-.0308 |
|
14 |
.6000 |
.0402 |
-.0208 |
14 |
.6000 |
. 0440 |
-.0246 |
|
15 |
.7000 |
.0312 |
-.0136 |
15 |
.7000 |
. 0340 |
-.0164 |
|
lb |
.8000 |
. 0208 |
-.0069 |
16 |
.8000 |
.0225 |
-.0Д87 |
|
17 |
.8500 |
.0153 |
-.0042 |
17 |
.8500 |
.0165 |
-.0054 |
|
18 |
.9000 |
.0101 |
-.0021 |
18 |
.9000 |
.0109 |
-.0029 |
|
1? |
.9500 |
.0047 |
-.0006 |
19 |
.9500 |
. 0050 |
-.0009 |
|
20 |
1.0000 |
0.0000 |
0.0000 |
20 |
1.0000 |
0.0000 |
0.0000 |
|
HQ-1,0/10 |
HQ-1,5/8 |
||||||
|
X(i) |
Yo |
Yu |
_ |
X(i> |
Yo |
Yu |
|
|
0.0000 |
0 . UUOO |
1 |
0.0000 |
U. 0001) |
0 . OOUO |
||
|
2 |
.0050 |
. 0092 |
– .0070 |
2 |
.0050 |
. 0082 |
– .0048 |
|
3 |
.0125 |
.0141 |
-.0114 |
3 |
.0125 |
.0128 |
– .0082 |
|
4 |
.0250 |
. 0214 |
-.0166 |
4 |
.0250 |
.0189 |
-.0115 |
|
5 |
. 0500 |
. 0307 |
-.0228 |
5 |
.0500 |
. 0273 |
-.0156 |
|
6 |
. 1000 |
.0421 |
-.0301 |
6 |
.1000 |
. 037V |
-.0199 |
|
7 |
. 1500 |
. 0499 |
-.0351 |
7 |
.1500 |
. 0451 |
– . 0229 |
|
8 |
.2000 |
. 0540 |
-.0375 |
8 |
.2000 |
.0489 |
– . 0243 |
|
V |
.2500 |
. 0569 |
-.0393 |
9 |
.2500 |
. 0517 |
-.Ubjj |
|
10 |
.3000 |
. 0586 |
-.0400 |
10 |
.3000 |
.0534 |
-.0255 |
|
11 |
.3500 |
. 0596 |
-.0404 |
11 |
.350 0 |
. 0544 |
-.0256 |
|
12 |
.4000 |
.0589 |
-.0393 |
12 |
.4000 |
.0534 |
-.0246 |
|
13 |
.5000 |
.0554 |
-.0354 |
13 |
.5000 |
.0513 |
-.0213 |
|
14 |
.6000 |
. 0478 |
-.0284 |
14 |
.6000 |
. 0450 |
– . 0159 |
|
15 |
.7000 |
.0368 |
-.0192 |
15 |
.7000 |
.0356 |
-.0092 |
|
16 |
.8000 |
.0243 |
-.0104 |
16 |
.8000 |
.0243 |
-.0035 |
|
17 |
.8500 |
.0177 |
-.0066 |
17 |
.8500 |
.0181 |
-.0014 |
|
18 |
.9000 |
.0117 |
-.0037 |
18 |
.9000 |
.0121 |
-.0002 |
|
19 |
.9500 |
.0054 |
-.0013 |
19 |
.9500 |
.0057 |
-.0004 |
|
20 |
1.0000 |
0.0000 |
0.0000 |
20 |
1.0000 |
0.0000 |
0.0000 |
U5/» І7І —
HQ-1,5/9 HQ-1,5/10
X (i) Yo Yu X(l) Yo Yu
HQ-2^/8
SD7032
SD7037
|
1 |
1.00000 |
0.00000 |
17 |
0.44745 |
0.07211 |
33 |
0.00127 |
-.00393 |
49 |
0.60914 |
-.00549 |
|
2 |
0.99672 |
0.00042 |
18 |
0.39862 |
0.07410 |
34 |
0.00806 |
-.00839 |
50 |
0.66197 |
-.00349 |
|
3 |
0.98707 |
0.00180 |
19 |
0.35101 |
0.07504 |
35 |
0.02038 |
-.01227 |
51 |
0.71305 |
-.00168 |
|
4 |
0.97146 |
0.00436 |
20 |
0.30508 |
0.07488 |
36 |
0.03800 |
-.01541 |
52 |
0.76178 |
-.00014 |
|
5 |
0.95041 |
0.00811 |
21 |
0.26125 |
0.07358 |
37 |
0.06074 |
-.01777 |
53 |
0.80752 |
0.00104 |
|
6 |
0.92450 |
0.01295 |
22 |
0.21989 |
0.07113 |
38 |
0.08844 |
-.01934 |
54 |
0.84964 |
0.00182 |
|
7 |
0.89425 |
0.01865 |
23 |
0.18137 |
0.06754 |
39 |
0.12084 |
-.02017 |
55 |
0.88756 |
0.00220 |
|
8 |
0.86015 |
0.02490 |
24 |
0.14601 |
0.06286 |
40 |
0.15765 |
-.02032 |
56 |
0.92071 |
0.00218 |
|
9 |
0.82261 |
0.03141 |
25 |
0.11410 |
0.05715 |
41 |
0.19850 |
-.01987 |
57 |
0.94859 |
0.00185 |
|
10 |
0.78201 |
0.03788 |
26 |
0.08586 |
0.05049 |
42 |
0.24296 |
-.01891 |
58 |
0.97077 |
0.00132 |
|
11 |
0.73865 |
0.04413 |
27 |
0.06146 |
0.04300 |
43 |
0.29055 |
-.01754 |
59 |
0.98690 |
0.00071 |
|
12 |
0.69294 |
0.05011 |
28 |
0.04102 |
0.03486 |
44 |
0.34071 |
-.01586 |
60 |
0.99671 |
0.00021 |
|
13 |
0.64539 |
0.05572 |
29 |
0.02462 |
0.02632 |
45 |
0.39288 |
-.01396 |
61 |
1.00001 |
0.00000 |
|
14 |
0.59655 |
0.06085 |
ЗО |
0.01232 |
0.01770 |
46 |
0.44643 |
-.01190 |
|||
|
15 |
0.54693 |
0.06538 |
31 |
0.00418 |
0.00936 |
47 |
0.50074 |
-.00976 |
|||
|
16 |
0.49706 |
0.06917 |
32 |
0.00021 |
0.00185 |
48 |
0.55519 |
-.00760 |
SD7090
|
1 |
1.00000 |
0.00000 |
17 |
0.43649 |
0.06457 |
33 |
0.00345 -.00734 |
49 |
0.61442 |
-.01948 |
|
2 |
0.99655 |
0.00050 |
18 |
0.38699 |
0.06674 |
34 |
0.01238 -.01318 |
50 |
0.66605 |
-.01658 |
|
3 |
0.98664 |
0.00219 |
19 |
0.33890 |
0.06795 |
35 |
0.02624 -.01834 |
51 |
0.71605 |
-.01363 |
|
4 |
0.97113 |
0.00512 |
20 |
0.29269 |
0.06814 |
36 |
0.04514 -.02262 |
52 |
0.76381 |
-.01083 |
|
5 |
0.95062 |
0.00882 |
21 |
0.24878 |
0.06724 |
37 |
0.06903 -.02605 |
53 |
0.80869 |
-.00829 |
|
6 |
0.92522 |
0.01284 |
22 |
0.20759 |
0.06522 |
38 |
0.09771 -.02873 |
54 |
0.85007 |
-.00609 |
|
7 |
0.89500 |
0.01718 |
23 |
0.16945 |
0.06206 |
39 |
0.13087 -.03067 |
55 |
0.88735 |
-.00426 |
|
8 |
0.86036 |
0.02188 |
24 |
0.13467 |
0.05780 |
40 |
0.16817 -.03188 |
56 |
0.92001 |
-.00279 |
|
9 |
0.82176 |
0.02691 |
25 |
0.10352 |
0.05249 |
41 |
0.20926 -.03240 |
57 |
0.94757 |
-.00160 |
|
10 |
0.77972 |
0.03218 |
26 |
0.07624 |
0.04621 |
42 |
0.25371 -.03229 |
58 |
0.96974 |
-.00066 |
|
11 |
0.73479 |
0.03760 |
27 |
0.05297 |
0.03907 |
43 |
0.30106 -.03161 |
59 |
0.98622 |
-.00009 |
|
12 |
0.68754 |
0.04304 |
28 |
0.03384 |
0.0312S |
44 |
0.35077 -.03046 |
60 |
0.99650 |
0.00004 |
|
13 |
0.63860 |
0.04834 |
29 |
0.01891 |
0.02298 |
45 |
0.40227 -.02889 |
61 |
1.00001 |
0.00000 |
|
14 |
0.58850 |
0.05329 |
ЗО |
0.00827 |
0.01458 |
46 |
0.45499 -.02696 |
|||
|
15 |
0.53777 |
0.05773 |
31 |
0.00196 |
0.00637 |
47 |
0.50832 -.02472 |
|||
|
16 |
0.48692 |
0.06153 |
32 |
0.00005 |
-.00097 |
48 |
0.56166 -.02221 |
SD8000
[1] N. A.C. A., National Advisory Committee for Aeronautics, U. S.A., now replaced by N. A.S. A.
[2] For explanation of the first, second and third digits of these aerofoils, see Chapter 9.
[3] The author is grateful to Andy Lennon for drawing his attention to this work and for subsequent discussions of it.











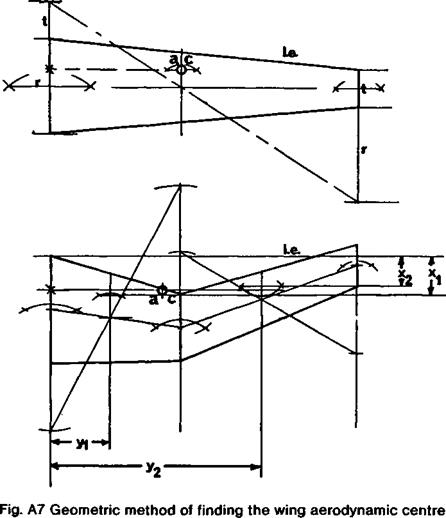
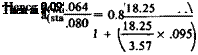
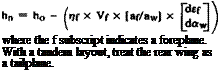
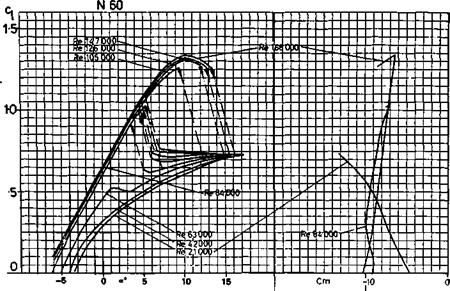
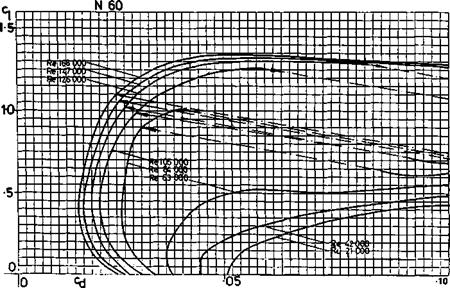
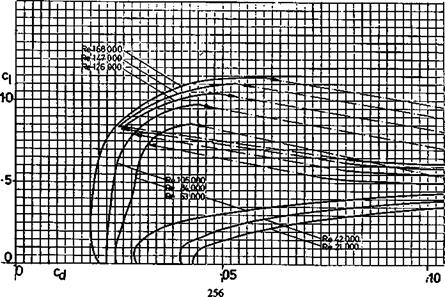
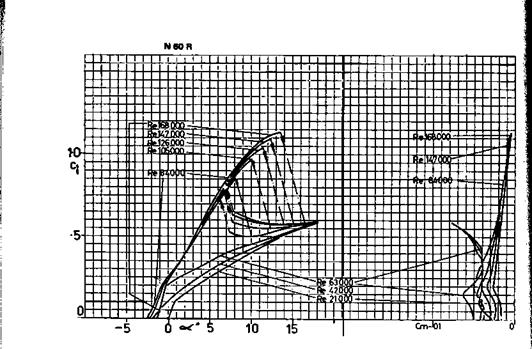
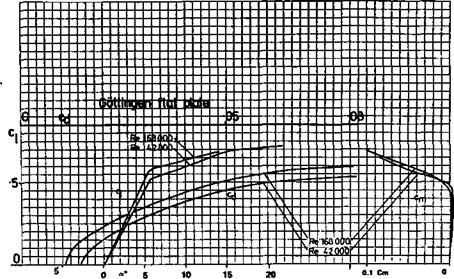
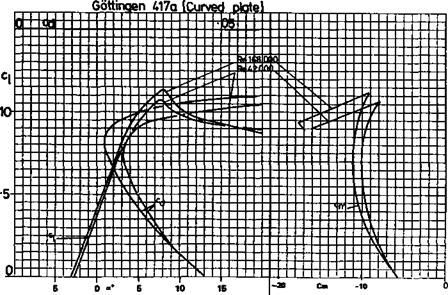
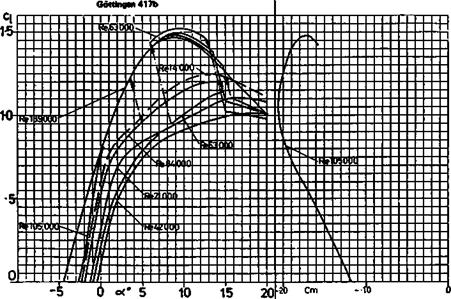
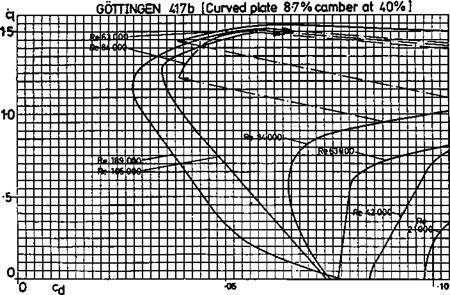
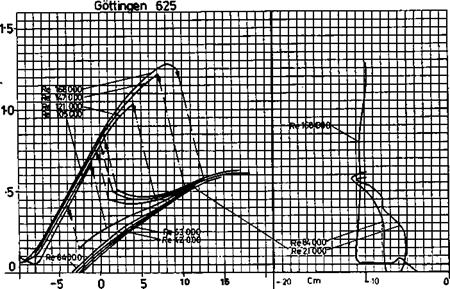
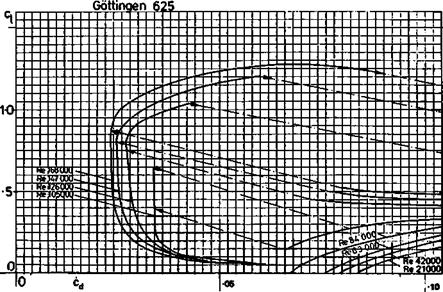
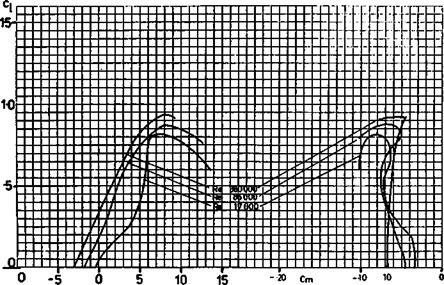
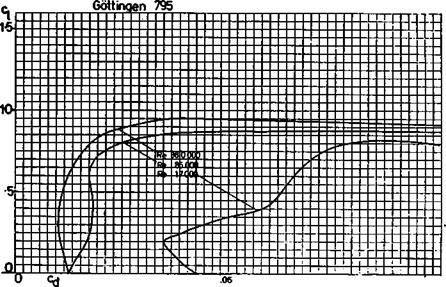
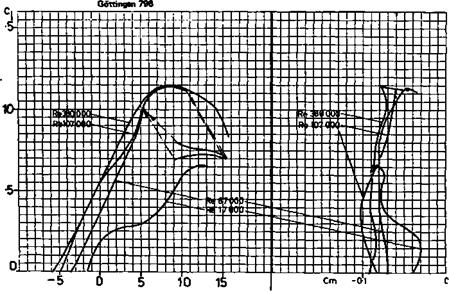
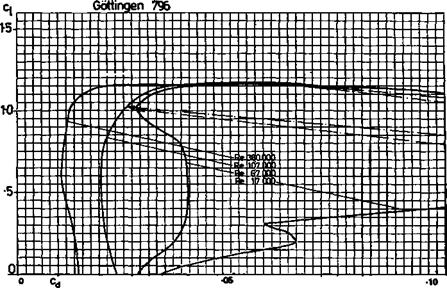
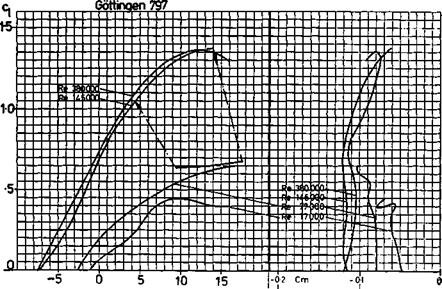
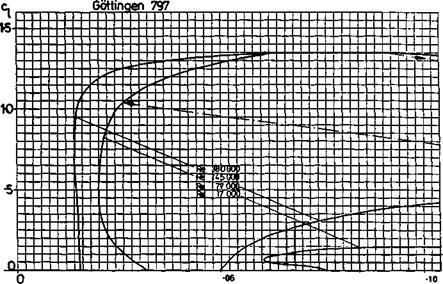
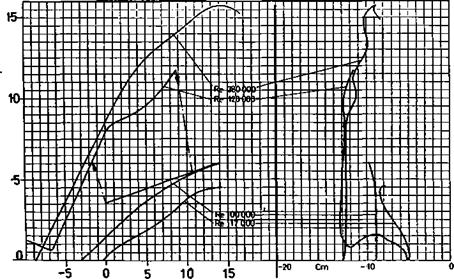
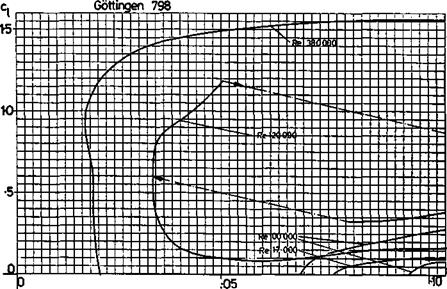
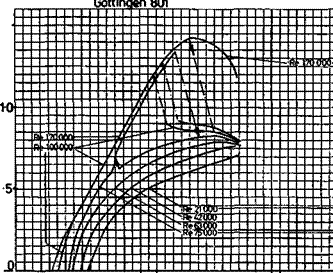
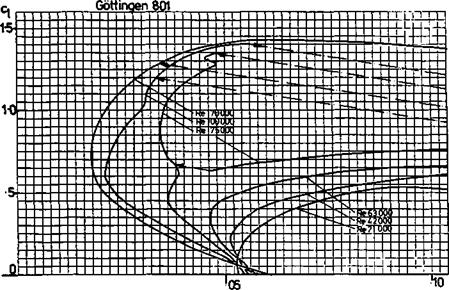
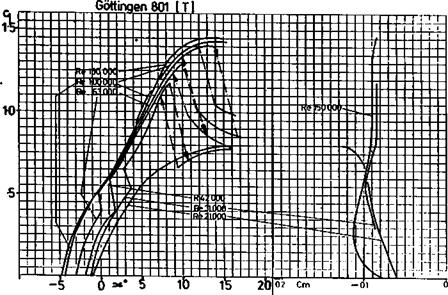
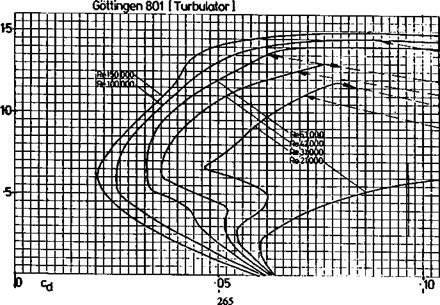
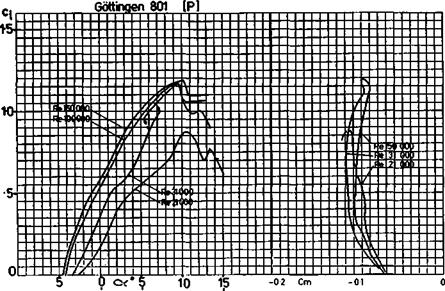
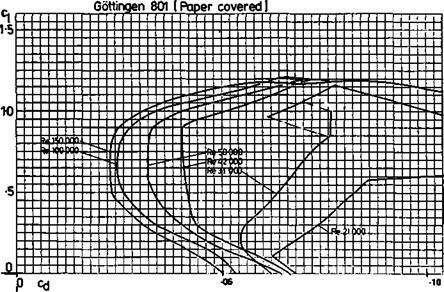
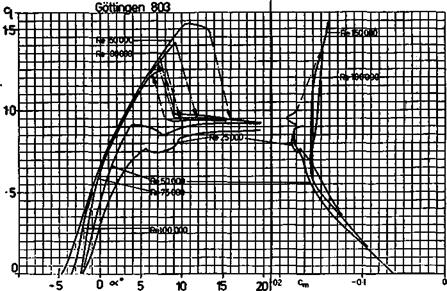
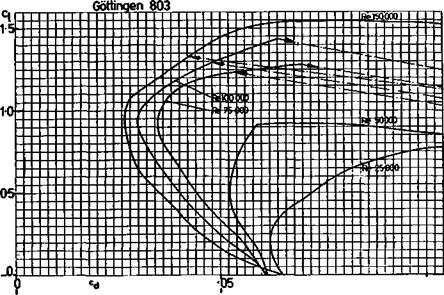
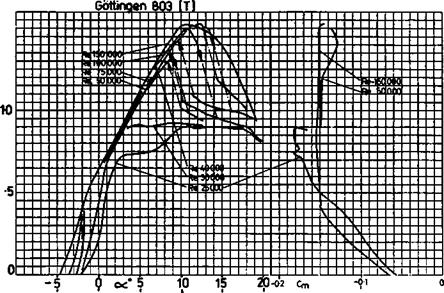
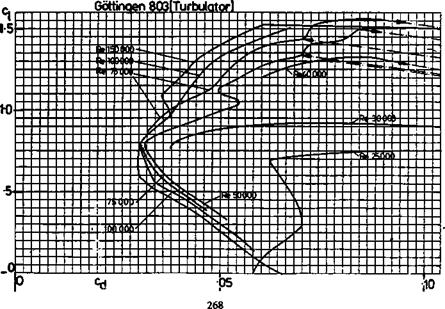
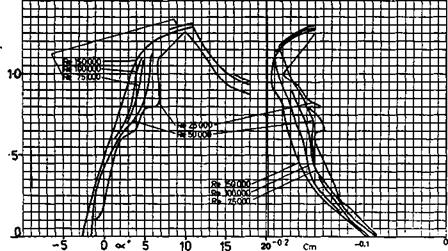
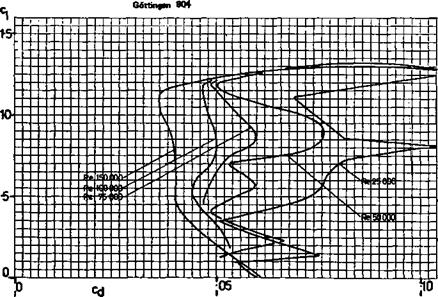
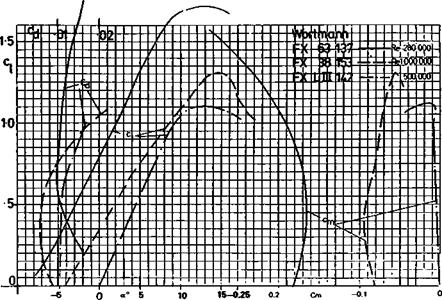
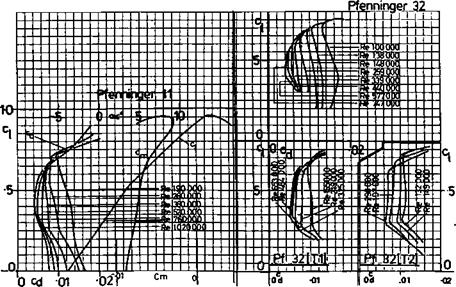
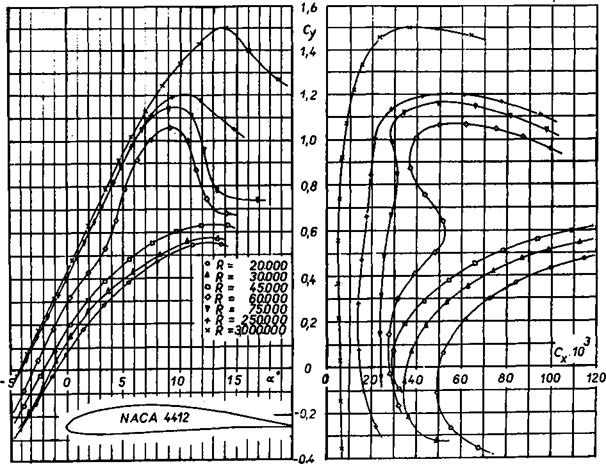
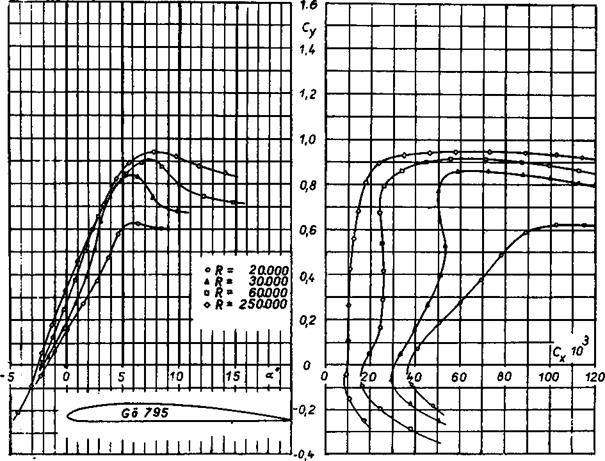
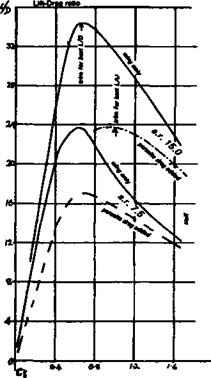
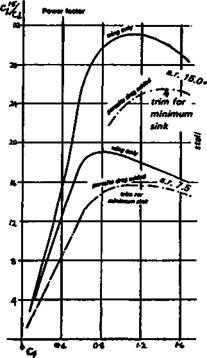
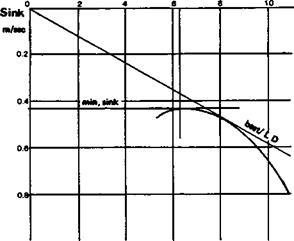

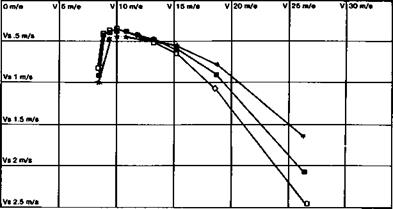
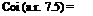
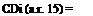 CL2 = CL2
CL2 = CL2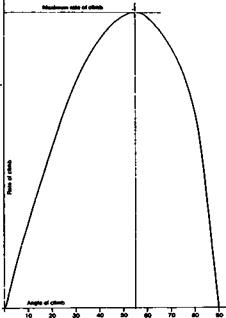
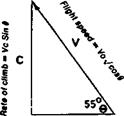
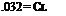 A flight speed of 50 metres/sec yields: 9.81
A flight speed of 50 metres/sec yields: 9.81 Sinking speed =
Sinking speed =