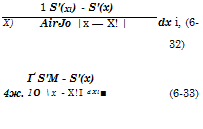An elementary illustration of the ideas of the foregoing section is provided by a two-dimensional vortex pair. We work here in terms of real variables rather than the complex variable, although it should be obvious to those familiar with two-dimensional flow theory that the results we obtain could be more conveniently derived by the latter approach. Consider a pair of vortices, which are equal and opposite and may be thought of as wrapped around very small circular cylindrical cores which constitute the boundaries S (Fig. 2-9). This motion can be generated by applying a downward force per unit area
ДР = —p ДФ = рГ (2-97)
across the barrier shown in the picture. The total Kelvin impulse per
|
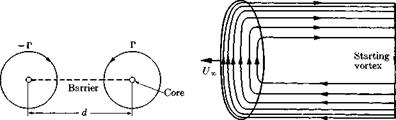
Fig. 2-9. Two equal and opposite line Fig. 2-10. Vortex pattern simulating vortices separated a distance d. flow around a wing of finite span.
|
unit distance normal to the page is directed downward and may be written
£ = – j(prd), (2-98)
where j is a unit upward vector and d is the instantaneous separation of the vortex cores.
If, for instance, one of the two vortices is bound to a wing moving to the left with velocity t/„ while the other remains at rest in the fluid in the manner of a starting vortex, the force exerted by the fluid on the supporting bodies is
Fbody = ~ ~it= ~ Jt
= )PTjt(d) = pU„Tj. (2-99)
This may be recognized as the two-dimensional lift called for by the theorem of Kutta and Joukowsky.
A more complicated system of vortices is used as an indirect means of representing the influence of viscosity on the flow around a lifting wing of finite span (Fig. 2-10). For any one of the infinite number of elongated vortex elements, the Kelvin impulse is directed downward and equals
£ = —jp ДФ X [area]. (2-100)
The area here changes at a rate dependent on the forward speed C7„. The reaction to the force producing the increased impulses of the various vortices adds up to the instantaneous lift on the wing. Moreover, from the spanwise distribution of vortex strengths the spanwise distribution of lift is obtainable, and the energy in the vortex system is connected with the induced drag of the wing. It is evident that these vortices could not be generated in the first place except through the action of viscosity in producing a boundary layer on the wing, yet we can obtain much useful information about the loading on the system without actually attempting a full solution of the equations of Navier and Stokes.
2-Q Two-Dimensional, Constant-Density Flow: Fundamental Ideas
We now turn to the subject of two-dimensional, irrotational, steady or unsteady motion of constant-density fluid. We begin by listing a number of results which are well-known and may be found developed, for instance, in Chapters 5 through 7 of Milne-Thompson (1960). The combined conditions of irrotationality and continuity assure the existence of a velocity potential Ф(г, t) and a stream function Ф(г, t), such that
Q = V4> = V X (кФ). (2-101)
Here
r = xi + yj. (2-102)

If (2-101) is written out in component form, we obtain.
The latter equalities will be recognized as the Cauchy-Riemann relations. For constant-density fluid,
V. Q = V2$> (2-104)
is the volume divergence, whereas for a rotational flow,
V X Q = – кУ2Ф (2-105)
is the vorticity vector. Therefore, in the case under consideration,
V4 = 0 = V24>. (2-106)
Among other ways of constructing solutions to the two-dimensional Laplace equation, a function of either
|
Z = x + iy = re’9
|
(2-107)
|
|
Z = x — iy = re-‘9
|
(2-108)
|
alone will be suitable.[3] To be more specific, the Cauchy-Riemann relations are necessary and sufficient conditions for Ф and Ф to be the real and imaginary parts, respectively, of the same analytic function of Z. This function we call the complex potential,
 ■w (Z) = Ф + г’Ф.
■w (Z) = Ф + г’Ф.
The following formulas for particle velocity and speed are easily derived:
The lines Ф = const and Ф = const form orthogonal networks of equi – potentials and streamlines in the x, у-plane, which is usually referred to as the Z-plane.
An interesting parallelism between the imaginary unit г = %/—l and the vector operator kx is discussed in Milne-Thompson (1960), and some readers may find it helpful to study this more physical interpretation of a quantity which has unfortunately been given a rather formidable name.
The fact that the complex potential is a function of a single variable has many advantages. Differentiation is of the ordinary variety and can be conveniently cascaded or inverted. Also, it makes little difference whether we operate with the functional relationship W(Z) orZ(W); many flows are more conveniently described by the latter.
We recall that many fundamental flow patterns are associated with simple singular forms of the complex potential. Thus In (Z) implies a point source or point vortex, 1/Z is a doublet, and Z“ corresponds to various fluid motions with linear boundaries meeting at angles related to a. A failure of one or more of the underlying physical assumptions occurs at the singular point location. Nevertheless, the singular solutions are useful in constructing flows of practical interest in regions away from their centers. Forces and moments can be expressed in terms of contour integrals around the singularities and are therefore connected with residues at poles.
The complex potential is itself a kinematical concept. To find pressures and resultant forces in steady and unsteady flows, further information is required. Thus Bernoulli’s equation, (1-63), is our tool for pressure calculation. The necessary quantities are taken from (2-111) and
where the operator on the right means to take the real part of the quantity in braces.
For forces and moments on a single closed figure in steady flow, we have available the classical Blasius equations
where Mo is the counterclockwise moment exerted by the fluid on the profile about an axis through the origin, and C is a contour that surrounds the body but no other singularities of the flow field, if such exist. In the absence of external singularities, the contour may be enlarged indefinitely. Then if ‘W(Z) can be expanded into an inverse power series in Z, which is nearly always the case, we identify all forces as coming from the l/Z term and all moments as coming from the l/Z2 term. We conclude that an effective source or vortex, plus a uniform stream, will lead to a resultant force. Moreover, a doublet may give rise to a moment, as can certain other combinations of source-like and vortex-like singular solutions.
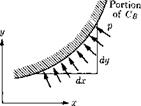 Fig. 2-11. Pressure force acting on a short segment of body surface in twodimensional flow.
Fig. 2-11. Pressure force acting on a short segment of body surface in twodimensional flow.
In a limited way, (2-113) and (2-114) can be extended to apply to unsteady flows. The development follows Section 6.41 of Milne-Thompson (1960), but a restriction is required which is not carefully stated there. Let us consider a two-dimensional body whose position is fixed and whose contour does not change with time but which is in an accelerated stream U„(t) or otherwise unsteady regime. See Fig. 2-11. We derive the force equation and simply write down its analog for the moment. Let Cb be a contour coinciding with the fixed body surface. We note that
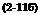 p<W<№_ дФ 2 dZ dZ P dt ‘
p<W<№_ дФ 2 dZ dZ P dt ‘
The quantity labeled “nonessential increment” is dropped from (2-116) since even a time function will contribute nothing to the total force or moment. We substitute into (2-115)
dFx – і dFy = » I % (2-H7)
On the body surface,
Ф = Фв(<) (2-118)
independent of the space coordinates because of the assumed fixed position (i. e., the body is always an instantaneous streamline). Noting that the integration of force is carried out for a particular instant of time, we may write, following the contour Cb,
dw = <M> = dW = dZ, (2-119)
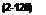
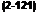 ЭФ _ dW. d*B dt ~ dt +l dt ‘
ЭФ _ dW. d*B dt ~ dt +l dt ‘
The latter holds true because
W = Ф — г’Ф.
Finally, we integrate around the contour С в and observe that the integral of the quantity d^fe/dt must vanish.
In this latter form the integrals are carried out around the contour C because each integrand is recognized as an analytic function of the variable of integration only, and contour deformation is permitted in the usual fashion. Of course, no pole singularities may be crossed during this deformation, and branch points must be handled by putting suitable cuts into the field. The extended Blasius equation for moments in unsteady flow reads
M0 = – Re j| £ Z (^f )2 dZ + p I £ fw + itB(t)]Z dzj • (2-123)
Here the second contour may not be deformed from Cb since Z is not an analytic function of Z.
We close this section by setting down, without proof, the two-dimensional counterpart of (2-28). For an arbitrary field point x, y, this theorem expresses the velocity potential as follows:
Here the fluid must be at rest at infinity; line integration around the body contour is carried out with respect to dummy variables x, y\ and
The natural logarithm of r is the potential of a two-dimensional line source centered at point X, y. When differentiated with respect to outward normal n, it is changed into a line doublet with its axis parallel to n.
2-10 Two-Dimensional, Constant-Density Flow:
Conformal Transformations and Their Uses
A consequence of the mapping theorem of Riemann is that the exterior of any given single closed figure, such as an airfoil, in the complex Z-plane can be mapped into the exterior of any other closed figure in the f-plane by an analytic relation of the form
£ = /(f)- (2-126)
See Fig. 2-12. It is frequently convenient to choose a circle for the f-figure. The angle between any two intersecting lines is preserved by the transformation; for example, a set of orthogonal trajectories in one plane also turns out to be a set in the other. If the point at infinity is to remain unchanged, the transformation can always be expanded at large distances into something of the form
2 = f + y + p + — -> (2-127)
where the a„ are complex constants.
|

Fig. 2-12. An illustration of the Z – and f-planes connected through conformal transformation.
|
It is occasionally pointed out that a special case of conformal transformation is the complex potential itself, (2-109), which can be regarded as a mapping of the streamlines and equipotentials into а (Ф + id’j-plane, where they become equidistant, horizontal and vertical straight lines, respectively.
The practical significance of the mapping theorem is that it can be used to transform one irrotational, constant-density flow’Wi(f) with elementary
boundaries into a second flow
W(Z) = ‘Wi[f1(Z)]l (2-128)
which has a more complicated boundary shape under the control of the transformer. Contours of engineering interest, such as a prescribed wing section, are readily obtained by properly choosing the function in (2-126). Conditions far away from the two figures can be kept the same, thus allowing for a prescribed flight condition.
Velocities, and consequently pressures, can be transformed through the relation
£ and – q being the real and imaginary parts of f, respectively. The equations of Blasius can be employed to determine resultant force and moment in either of the two planes, and the transformation of variable itself is helpful when determining this information for the Z-figure. To provide starting points, many elementary complex potentials are known which characterize useful flows with circular boundaries.
Several transformations have proved either historically or currently valuable for constructing families of airfoil shapes and other two-dimensional figures with aeronautical applications. The reader is presumed to be familiar with the Joukowsky transformation, and much can be done with very minor refinements to the original investigations of Kutta and Joukowsky. No effort is made to expose in detail the various steps that have been carried out by different investigators, but we do list below a number of the more important transformations and something about their consequences.
1. The Joukowsky-Kutta Transformation
Z=[ + j – (2-131)
Here l is a positive real constant, and the so-called singular points of the transformation where the dZ/d{ — 0 are located at f = ±1, corresponding to Z = ±21. When applied to suitably located circles in the f-plane, (2-131) is well known to produce ellipses, flat plates, circular arc profiles of zero thickness, symmetrical and cambered profiles with their maximum thickness far forward and with approximately circular-arc camber lines.
The shape obtained actually depends on the location of the circle relative to the aforementioned singular points. A cusped trailing edge is produced by passing the circle through the singular point on the downstream side of the circle.
2. The von Mises Transformations. These transformations are special cases of the series, (2-127), in which it is truncated to a finite number of terms:
Z=f + ^ + — -+ £- (2-132)
S f”
When an airfoil is being designed, the series is constructed by starting from the singular point locations at
and subsequently integrated in closed form. By the rather laborious process of trial-and-error location of singular points, many practical airfoils were developed during the 1920’s. It is possible to adjust the thickness and camber distributions in a very general way. Interesting examples of von Mises and other airfoils will be found discussed in a recent book by Riegels (1961).
3. The von Karman-Trefftz Transformation. This method derives from a scheme for getting rid of the cusp at the trailing edge, produced by the foregoing classes of transformations, and replacing it by a corner with a finite angle t. To see how it accomplishes this, consider a transformation with a singular point at f = fo, corresponding to a point Z = Z0. In the vicinity of this particular singular point, it is easy to show that the transformation can be approximated by
Z-Z0= Alt – ГоГ, n > 1, (2-135)
where A is some complex constant. Evidently, the quantity
S = – ~Ai’ – f°r" (2“136)
vanishes at the point for n > 1, as it is expected to do. Let r0 and в0 be the modulus and argument of the complex vector emanating from the point f0- Equation (2-136) can be written
 d(Z – Z0) = nAr3-V("-1)*0d(r – fo).
d(Z – Z0) = nAr3-V("-1)*0d(r – fo).
This is to say, the element of arc d((" — f0) is rotated through an angle (n — 1)0O in passing from the ("-plane to the Z-plane, if we overlook the effect of the constant A which rotates any line through ("0 by the same amount. Figure 2-13 demonstrates what this transformation does to a continuous curve passing through the point (" = ("0 in the ("-plane. By proper choice of n, the break in the curve which is produced on the Z-plane can be given any desired value between ir and 27t.
Yon K&rm&n and Trefftz (1918) suggested replacing (2-138) as follows:
As in Fig. 2-14, the outer angle between the upper and lower surfaces of the airfoil at its trailing edge (T. E.) is now (2тг — т), so a finite interior angle has been introduced and can be selected at will.
In a similar fashion a factor
can be included in the von Mises equation (2-134). Then if the circle in the f-plane is passed through the point f = f,,T E, an adjustable trailing edge is provided for the resulting profile.
4. The Theodor sen Transformation[4] Theodorsen’s method and the several extensions which have been suggested for it are capable of constructing the flow around an airfoil or other single object of completely arbitrary shape. All that is needed is some sort of table or equation providing the ordinates of the desired figure. The present brief discussion will emphasize the application to the airfoil.
The transformation is actually carried out in two steps. First the airfoil is located in the Z-plane as close as possible to where a similarly shaped Joukowsky airfoil would fall. It can be proved that this will involve locating the Joukowsky singular points Z = ±2Z halfway between the nose and the trailing edge and their respective centers of curvature. (Of course, if the trailing edge is pointed, the singularity Z — —21 falls right on it.) By applying Joukowsky’s transformation in reverse, the airfoil is transformed into a “pseudocircle” in the Z’-plane
Z = Z> + D • (2-140)
z
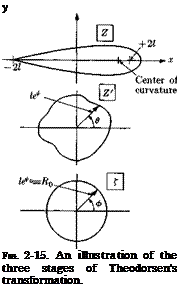 The second procedure is the conversion of the pseudocircle to an exact circle centered at the origin in the Z’-plane by iterated determination of the coefficients in the transformation series
The second procedure is the conversion of the pseudocircle to an exact circle centered at the origin in the Z’-plane by iterated determination of the coefficients in the transformation series
Z’= fexpfe^). (2-141)
i=i 1 7
Here the Cn are complex constants. The two steps of the process are illustrated in Fig. 2-15.
Let us consider the two steps in a little more detail. We write
Z = x + iy, (2-142)
Z> = іеФ+іч, (2-143)
That is, the argument of Z’ is
denoted by в and its modulus is le*. It is not difficult to derive the direct and inverse relationships between the coordinates of the airfoil and pseudocircle:
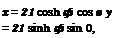 (2-144)
(2-144)
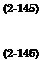 2 sin2 в = p + л/p2 + (y/l)2
2 sin2 в = p + л/p2 + (y/l)2
2 sinh2 ф = — p – f – Vp2 + (y/l) 2>
where
Note that ф will be quite a small number for profiles of normal thickness and camber.
The function ф(в) for the pseudocircle may be regarded as known at as many points as desired. We then write
J – = Д0еіф = и*°еіф. (2-147)
For points on the two contours only, the transformation, (2-141), can be manipulated as follows:
Z’ le^+i8
J = = exP к* – *o) + W – Ф)}, (2-148)
Z’ = f exp [{ф — фо) + i(8 — ф)] = f exp ^ (2-149)
Theodorsen (1931) adopted the symbol e to denote the shift in argument going from the Z’- to the ("-plane,
 € ~ ф — в ОГ ф = в + €.
€ ~ ф — в ОГ ф = в + €.
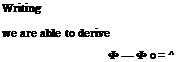 Cn ~ “1“
Cn ~ “1“
An. Bn.
—– COS пф І———- sm пф
п туп
0 Ло J
Bn, і An • ,
— cos пф H—— sm пф
п ТУП
о Ло J
These two equations imply that (ф — Фа) and e are conjugate quantities. They are expressed as Fourier series in the variable Ф, so that the standard formulas for individual Fourier coefficients could be employed if these quantities were known in terms of ф. Moreover, the conjugate property
|
can be used to relate the functions e and ф directly,
|
as follows:
|
|
|
■<*’>- Li *<+>“*(* 2*
|
^ёф,
|
(2-154)
|
|
|
|
|
Ф(Ф’) = ^ + ~fo е(ф) cot^
|
ф’)ёф.
|
(2-155)
|
In actuality, only ф(в) is available to begin with; 0 can be regarded as a first approximation to ф, however, and (2-154) employed to get a first estimate of e. Equation (2-150) then yields an improved approximation to ф and to ф(ф), so that (2-154) may be used in an iterative fashion to obtain converged formulas for the desired quantities. For typical airfoils it is found that this process converges very rapidly, and the numerical integration of (2-154) need be iterated only once or twice. Of course, it is necessary to be careful about the pole singularity at ф = ф’.
As described in the references, Theodorsen’s so-called e-method has many uses in the theory of low-speed airfoils. For instance, one can generate families of profiles from assumed forms of the function е(ф). Approximate means have been developed, starting from an airfoil of known shape and pressure distribution, for adjusting this pressure distribution in a desired fashion. This scheme formed the basis for the laminar flow profiles
|
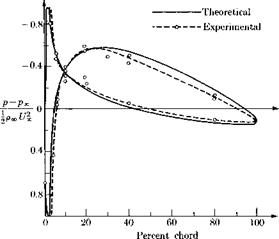
Fig. 2-16. Comparison between predicted and measured pressure distribution over the upper and lower surfaces of a Clark Y airfoil at an effective geometrical incidence of —1 deg 16 min. Theoretical incidence chosen to give approximately the measured value of total lift. [Adapted from Theodorsen (1931).]
|
which played such an important role in the early 1940’s. Their shapes sustain a carefully adjusted, favorable pressure distribution to assure the longest possible laminar run prior to transition in the boundary layer. In wind tunnel tests, they achieve remarkable reductions in friction drag; unfortunately, these same reductions cannot usually be obtained in engineering practice, and some of the profiles have undesirable characteristics above the critical flight Mach number.
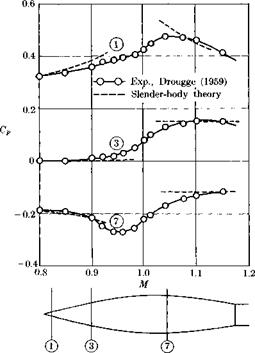
Figure 2-16 shows a particularly successful example of the comparison between pressure distribution measured on an airfoil and predicted by this so-called “e-method.”
5. The Schwarz-Christoffel Transformations. These transformations are described in detail in any advanced text on functions of a complex variable. They furnish a useful general technique for constructing flows with boundaries which are made up of straight-line segments.
![]() <P = — – gzu{x — Be) for z > 0 <P = ^zi(x + Bz) for z < 0.
<P = — – gzu{x — Be) for z > 0 <P = ^zi(x + Bz) for z < 0.
![]()











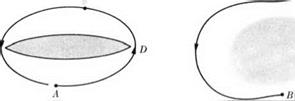

 Fig. 2-11. Pressure force acting on a short segment of body surface in twodimensional flow.
Fig. 2-11. Pressure force acting on a short segment of body surface in twodimensional flow.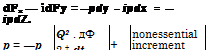


 The second procedure is the conversion of the pseudocircle to an exact circle centered at the origin in the Z’-plane by iterated determination of the coefficients in the transformation series
The second procedure is the conversion of the pseudocircle to an exact circle centered at the origin in the Z’-plane by iterated determination of the coefficients in the transformation series Cn ~ “1“
Cn ~ “1“