Chapter Review
This chapter has summarized the various computational methods being used in the analysis of helicopter problems. The important role of computational fluid dynamics, particularly in the form of the Navier-Stokes equations, in better understanding problems in helicopter aerodynamics has been emphasized. To some, the use of “CFD” is held out to be the salvation for the helicopter aerodynamicist, but this is a misleading perspective. CFD will ultimately prevail for the complete simulation of the flow about a helicopter, but there are still many fundamental numerical and practical issues to be resolved, least of all is in the proper and efficient coupling of the CFD to the dynamic and elastic structural motion of the various components of the helicopter. The preservation of vorticity over many rotor revolutions is clearly one key to providing better CFD models of the rotor wake. The development of more general and more adaptable turbulence closure models must also continue, particularly as they apply to describing the vortical nature of rotor wakes and the structure of the blade tip vortices. Such issues are important in better understanding a whole host of practical helicopter flight problems such as descending flight, maneuvers, flight in the VRS or in autorotation, interactional aerodynamics between various airframe components, flight near the ground and many problems in rotor vibration and acoustics. Meantime, these problems require immediate or shorter term solution capabilities, and it is unrealistic to expect these problems to wait in the sidelines until pure CFD reaches the required level of maturity. Meantime, more parsimonious aerodynamic models must continue to be developed, with the ideal of fusing together the capabilities of the best available models.
It is fair to say that the large computer resources required, and the algorithmic challenges posed by modem CFD methods have thus far limited their use for many practical problems in helicopter design. This is especially the case for the Navier-Stokes and Euler-based methods. The community has invested heavily in a variety of CFD approaches, but the task of modeling the flow about a complete helicopter, or even just the rotor, is indeed truly
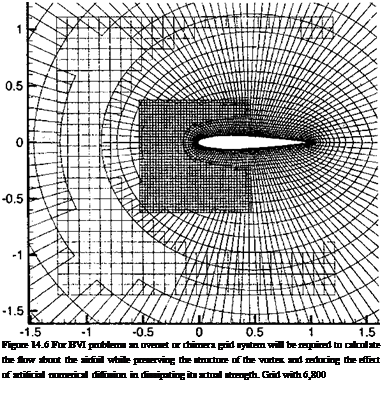
daunting. The various rotating and nonrotating aerodynamic components of a helicopter make generating appropriate grids on which to solve the equations a challenging problem in itself. Passing flow information back and forth between these grids requires special numerical algorithms and incurs significant computational cost. Until the grid generation process becomes more automated and can tackle complex geometries with ease, the use of many types of CFD methods will not lie in the domain of practicality for helicopter designers. Even then, validation of the models and resulting flow predictions requires extensive work and continues to offer challenges for the experimentalists in providing suitable quality surface and off-surface flow field measurements. Unless proper validation of its predictive capabilities can beensured, CFD cannot be assigned the confidence levels necessary for use in design, no matter how fundamentally sophisticated the method. These problems offer many new opportunities that are rich for new research.
There are other areas such as aeroelasticity and flight mechanics simulations, where the coupling of CFD into the solution process is less practical, at least in the shorter time. This is in part because of high computational costs and/or the difficulties in coupling different types of solution methodologies. How the helicopter actually flies comes under the domain of flight mechanics, and flight dynamics and handling qualities assessments may require a real-time or near real-time solution, rendering many “state-of-the-art” aerodynamic models impractical. Also, for some applications the equations describing the aerodynamics must be written in a specific mathematical form (as ordinary differential equations, for instance) to be compatible with the methods of analysis used for flight control system design. This is where the role of so-called “reduced-order” models can make significant inroads by avoiding the expense and difficulties of a complete CFD solution, yet much validation is required to gain confidence levels. The proper coupling and integration of aerodynamic methods of analysis into other disciplines of helicopter analysis is really the key to designing better helicopters. It is clear that the future offers many exciting opportunities for research focused toward the development of more innovative computational models with greater predictive capabilities. Only then can the problems that limit the performance and capabilities of the helicopter be understood and mitigated. Given the complexity of the helicopter flow field, it is likely that CFD methods for helicopter applications will reach maturity only long after their application within the fixed-wing community is accepted as standard practice.
[1] A branch of mechanics that deals with the motion of air and the effects on bodies.
[2] Understanding the basic aerodynamics of vertical flight. The theoretical power required to produce a fixed amount of lift was an unknown quantity to the earliest experimenters, who were guided more by intuition than by science. The first significant application of aerodynamic theory to helicopter rotors came about in the early 1920s. [See also Liberatore (1998) for a historical discussion of this point.]
[3] The lack of a suitable engine. This was a problem that was not to be overcome until the beginning of the twentieth century through the development of practical internal combustion (gasoline-powered) engines. The steam engine was never a viable concept for any type of aircraft. However, the development of internal
[4] A braccia is an old Florentine unit of measure, approximately equal to one arm’s length, although it has been defined variously between 15 and 39 in (0.28 to 1 m).
[5] Newton’s third law states that for every action (force) there is an equal and opposite reaction (force).
[6] In 1897, a British patent was to be granted to White (1898) for a vertically lifting machine with variable pitch (feathering) blades, but it was a windmill concept by Lewis & Lewis (1838) that probably saw the first use of a swashplate for blade pitch control on a rotating-wing.
[7] In addition, the content of the entire first issue of the Journal of the American Helicopter Soc., 1(1), Jan. 1956, was devoted to the early autogiro and helicopter developments in the United States.
[8] Of interest is the rotary engine built by Berliner in 1905, which predates the Le Rhone engine, and this
was built also with the specific purpose of installing it in a helicopter.
[9] The ability to autorotate is really a distinguishing feature of a successful and practical helicopter.
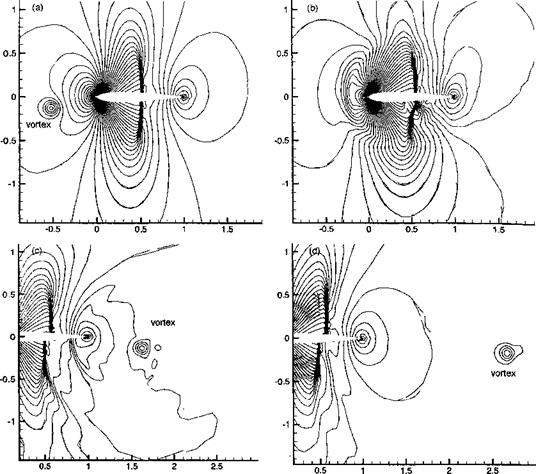
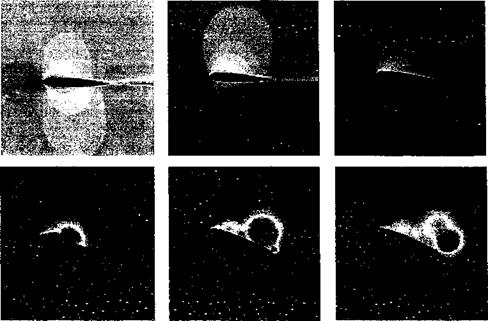
[10] This phenomenon is called blade vortex interaction or ВVI – see Chapters 8, 10, and 14.
[11] Meaning the slipstream is well downstream of the rotor at infinity or in the vena contracta, although in practice this may only be less than one rotor radius.
[12] From a piloting perspective the decrease in power requirements for flight found when moving from hover cause an excess power available and so the helicopter will climb. Pilots often call this climbing behavior “translational lift,” but the term is a misnomer because unless significant acceleration is involved, rotor lift equals helicopter weight and the helicopter climbs by virtue of the excess power available not from excess lift generation.
[13] Typically, a minimum of 20 elements must be used to ensure an adequate numerical resolution of the
inflow and spanwise loading, but 40 elements or more is desirable.
followed by a momentum balance using the conservation laws in integral form. This, however, is a technique valid only below stall where there are no viscous losses from rotation of the fluid (see Section 7.8 and Question 7.9).
[16] Measurements of 2-D section drag are often made by measuring the velocity in the wake of the airfoil,
[17] Normally in aerodynamics we use lower case subscripts to denote sectional values and subscripts in capitals to mean total or integrated quantities.
[18] Collective pitch: This input (6q) increases the main rotor blade pitch angles by the same amount, and, therefore, this changes the magnitude of the rotor thrust. The collective is changed by a lever that is held in the pilot’s left hand, with an upward pulling motion required for an increase in thrust. Increasing collective pitch also requires an increase in power. On some helicopters this requires the pilot to open the throttle (increasing fuel flow to the engine), which is operated by a twist-grip at the end of the collective lever. However, on most helicopters the fuel-flow is controlled by an engine governor, which automatically maintains rotor rpm at the regulated value as rotor torque required increases or decreases.
[19] Lateral and longitudinal cyclic pitch: These inputs impart a once-per-revolution cyclic pitch change to the blades. Lateral cyclic {0c) is applied such that the rotor disk can be tilted left and right. This changes the orientation of the rotor-thrust
[20] On tandems such as the CH-46 or CH-47 the rear rotor is placed substantially higher than the front rotor to minimize these interference effects.
[21] To a first approximation this can be assumed to be a fixed fraction of the main rotor power.
[22] 1 W3/2
R =——– —=——— . (6.53)
FM *j2jtp Pavail
Assuming a net aircraft and pilot weight of 200 lb (optimistic) and a rotor a figure of merit of 0.75 (also optimistic, even with the benefits of ground effect) operated at sea level conditions, then solving for the rotor radius gives more than 77 ft. It is probably unrealistic to build such a large single rotor with blades that are both lightweight and have sufficient strength and structural rigidity, although the attempt has been made. Multirotor machines may offer better prospects in this regard. Furthermore, because such a rotor will have blades that turn at a low rpm, the tip Reynolds numbers will be low and the viscous drag on the blades will be relatively high. It would seem unlikely, therefore, that such a rotor with a FM of 0.75 is realizable. However, it is interesting that if it were possible, such a rotor would have a disk loading of only 0.0107 lb/ft2 and an average induced velocity, Vh, of about 3 ft/s.
Filippone (2002) considers the possibility of two or more crew to power a HPH because this wilFdouble the effective power available. This is a variation of the engine selection problem previously introduced in Section 5.5.5. Yet because the crew weight will at least double, Eq. 6.53 shows that that the rotor radius will have to increase by at least a factor of 1.41 to maintain a low disk loading, and so empty airframe will also increase (i. e., an increase of the empty weight fraction.) This is a direct result of the square-cube law (see Section 6.4.1). The various trades, however, require further study for multirotor HPH configurations.
Any HPH must have a large diameter rotor operating in close proximity to the ground, so the issue of ground effect (see Section 5.8) on rotor performance must be carefully
[24] A high maximum lift coefficient, Qmax. This will allow a rotor with lower solidity and lighter weight, or will permit flight at higher rotor thrusts and under higher maneuver load factors.
[25] A high drag divergence Mach number. This will permit flight at high forward speeds without prohibitive power loss or increase in noise levels.
[26] The SC1095-R8 has a modified nose shape and a slightly smaller thickness-to-chord ratio than the SC 1095. For this reason, it is sometimes referred to as the SC1094-R8 – see Flemming (1982).
[27] This is called “dynamic stall” and is discussed in detail in Chapter 9.
[28] Notice that this case does not represent an oscillating airfoil in AoA because the pitch-rate terms are not included.
[29] The apparent mass contributions to the forces and pitching moments, which are proportional to the instantaneous motion, are often included as part of the quasi-steady result. If they are not, then the standard quasi-steady thin-airfoil result is obtained.
[30] By definition, an indicial function is the response to a disturbance that is applied instantaneously at time zero and held constant thereafter, that is, a disturbance given by a step function. In this case, w = 0 for t < 0 and w = Va for t > 0.
[31] For some applications the exponential approximation to the indicial response may not be considered adequate. This is usually because the rate of approach to the asymptotic value is not as correct for the exponential approximation compared to the exact behavior. This effect, however, is more of academic interest rather than of any practical importance.
[32] The Euler СГО method is computationally expensive, being approximately five orders of magnitude greater than the cost of the solution obtained using Duhamel superposition.
[33] Notice that in the thin-airfoil solution and also because low angles of attack are assumed, the normal force and lift force are usually used synonymously.
[34] The effects of the Reynolds number are generally implied, and the functional dependency will be omitted for brevity.
[35] This equation can be shown valid up to at least the critical Mach number of the airfoil, beyond which nonlinear effects do not allow such simple generalizations because of the development of transonic flow.
[36] Notice that there is some offset in the Cm curves, which has been attributed to thermal drift of the pressure transducers used in the experiment.
[37] Also note, that while the sound wavelets produced by each supersonic source point are nominally circular in form, they have been plotted here discretely and so have a reduced angular resolution.
[38] When negative aerodynamic torsional damping occurs, there is a possibility of aeroelastic problems on the rotor, including stall flutter. This effect is discussed quantitatively in Section 9.6.
[39] While high-speed, black & white film has been traditionally used, the use of a high-resolution digital
still or video camera is a common modern format.
[40] A vortex line is simply a curve in the fluid that is tangent to the local vorticity vector; it should not be confused with a line vortex. –
[41] This is probably the largest step size that will give a reasonable physical representation of the rotor wake problem without loss of numerical accuracy when using straight-line vortex filaments.
[42] Their performance, however, is certainly still not understood from a fundamental fluid mechanics point
of view.
[43] In the case without the body the rotor drive was covered with a fairing.
[44] This chapter is dedicated to the memory of Professor Alfred Gessow.
1 The name “Autogiro” was later to be coined by Juan de la Cierva as a trademarked name for his aircraft, so when referring specifically to the Cierva machines it is always appropriate to call them “Autogiros” with a capital “A.”
[45] Later autogiro designs incorporated the ability to tilt the rotor disk, either by tilting the rotor shaft
directly on a gimbal or with the use of a “spider” cyclic pitch mechanism.
[46] This is analogous to the helicopter rotor where the maximum operating figure of merit is obtained only
at one value of Cj or disk loading.
[47] It should be noted, however, that in the wind energy literature the blade section angle of attack is usually written as a = ф — в based on convention.
[48] Mach numbers are relatively low for a wind turbine and compressibility effects do not need to be considered.
[49] This chapter was co-written with Richard Brown of Imperial College, University of London.